圖的四種最短路徑算法

本文總結了圖的幾種最短路徑算法的實現：深度或廣度優先搜索算法，弗洛伊德算法，迪杰斯特拉算法，Bellman-Ford算法

1），深度或廣度優先搜索算法（解決單源最短路徑）
從起始結點開始訪問所有的深度遍歷路徑或廣度優先路徑，則到達終點結點的路徑有多條，取其中路徑權值最短的一條則為最短路徑。

下面是核心代碼：

[cpp]?view plain?copy

void?dfs(int?cur,?int?dst){????
????/***operation***/????
????
????/***operation***/????
????if(minPath?<?dst)?return;//當前走過路徑大于之前最短路徑，沒必要再走下去????
????if(cur?==?n){//臨界條件????
????????if(minPath?>?dst)?minPath?=?dst;????
????????return;????
????}????
????else{????
????????int?i;????
????????for(i?=?1;?i?<=?n;?i++){????
????????????if(edge[cur][i]?!=?inf?&&?edge[cur][i]?!=?0?&&?mark[i]?==?0){????
????????????????mark[i]?=?1;????
????????????????dfs(i,?dst+edge[cur][i]);????
????????????????mark[i]?=?0;??//需要在深度遍歷返回時將訪問標志置0??????????????
????????????}????
????????}????
????????return;????
????}????
}????

例1：下面是城市的地圖，注意是單向圖，求城市1到城市5的最短距離。(引用的是上次總結的圖論（一）中1）的例2)

[cpp]?view plain?copy

/***先輸入n個結點，m條邊，之后輸入有向圖的m條邊，邊的前兩元素表示起始結點，第三個值表權值，輸出1號城市到n號城市的最短距離***/????
/***算法的思路是訪問所有的深度遍歷路徑，需要在深度遍歷返回時將訪問標志置0***/????
#include?<iostream>????
#include?<iomanip>????
#define?nmax?110????
#define?inf?999999999????
using?namespace?std;????
int?n,?m,?minPath,?edge[nmax][nmax],?mark[nmax];//結點數，邊數，最小路徑，鄰接矩陣，結點訪問標記????
void?dfs(int?cur,?int?dst){????
????/***operation***/????
????
????/***operation***/????
????if(minPath?<?dst)?return;//當前走過路徑大于之前最短路徑，沒必要再走下去????
????if(cur?==?n){//臨界條件????
????????if(minPath?>?dst)?minPath?=?dst;????
????????return;????
????}????
????else{????
????????int?i;????
????????for(i?=?1;?i?<=?n;?i++){????
????????????if(edge[cur][i]?!=?inf?&&?edge[cur][i]?!=?0?&&?mark[i]?==?0){????
????????????????mark[i]?=?1;????
????????????????dfs(i,?dst+edge[cur][i]);????
????????????????mark[i]?=?0;????????????????
????????????}????
????????}????
????????return;????
????}????
}????
????
int?main(){????
????while(cin?>>?n?>>?m?&&?n?!=?0){????
????????//初始化鄰接矩陣????
????????int?i,?j;????
????????for(i?=?1;?i?<=?n;?i++){????
????????????for(j?=?1;?j?<=?n;?j++){????
????????????????edge[i][j]?=?inf;????
????????????}????
????????????edge[i][i]?=?0;????
????????}????
????????int?a,?b;????
????????while(m--){????
????????????cin?>>?a?>>?b;????
????????????cin?>>?edge[a][b];????
????????}????
????????//以dnf(1)為起點開始遞歸遍歷????
????????memset(mark,?0,?sizeof(mark));????
????????minPath?=?inf;????
????????mark[1]?=?1;????
????????dfs(1,?0);????
????????cout?<<?minPath?<<?endl;????
????}????
????return?0;????
}????

程序運行結果如下：

2），弗洛伊德算法（解決多源最短路徑）：時間復雜度O(n^3),空間復雜度O(n^2)
基本思想：最開始只允許經過1號頂點進行中轉，接下來只允許經過1號和2號頂點進行中轉......允許經過1~n號所有頂點進行中轉，來不斷動態更新任意兩點之間的最短路程。即求從i號頂點到j號頂點只經過前k號點的最短路程。

分析如下：1，首先構建鄰接矩陣Floyd[n+1][n+1]，假如現在只允許經過1號結點，求任意兩點間的最短路程，很顯然Floyd[i][j] = min{Floyd[i][j], Floyd[i][1]+Floyd[1][j]}，代碼如下：

[cpp]?view plain?copy

for(i?=?1;?i?<=?n;?i++){??
????for(j?=?1;?j?<=?n;?j++){??
????????if(Floyd[i][j]?>?Floyd[i][1]?+?Floyd[1][j])??
????????????Floyd[i][j]?=?Floyd[i][1]?+?Floyd[1][j];??
????}??
}??

2，接下來繼續求在只允許經過1和2號兩個頂點的情況下任意兩點之間的最短距離，在已經實現了從i號頂點到j號頂點只經過前1號點的最短路程的前提下，現在再插入第2號結點，來看看能不能更新更短路徑，故只需在步驟1求得的Floyd[n+1][n+1]基礎上，進行Floyd[i][j] = min{Floyd[i][j], Floyd[i][2]+Floyd[2][j]}；......
3，很顯然，需要n次這樣的更新，表示依次插入了1號，2號......n號結點，最后求得的Floyd[n+1][n+1]是從i號頂點到j號頂點只經過前n號點的最短路程。故核心代碼如下：

[cpp]?view plain?copy

#define?inf?99999999??
for(k?=?1;?k?<=?n;?k++){??
????for(i?=?1;?i?<=?n;?i++){??
????????for(j?=?1;?j?<=?n;?j++){??
????????????if(Floyd[i][k]?<?inf?&&?Floyd[k][j]?<?inf?&&?Floyd[i][j]?>?Floyd[i][k]?+?Floyd[k][j])??
????????????????Floyd[i][j]?=?Floyd[i][k]?+?Floyd[k][j];??
????????}??
????}??
}??

例1：尋找最短的從商店到賽場的路線。其中商店在1號結點處，賽場在n號結點處，1~n結點中有m條線路雙向連接。

[cpp]?view plain?copy

/***先輸入n，m，再輸入m個三元組，n為路口數，m表示有幾條路其中1為商店，n為賽場，三元組分別表起點，終點，該路徑長，輸出1到n的最短路徑***/??
#include?<iostream>??
using?namespace?std;??
#define?inf?99999999??
#define?nmax?110??
int?edge[nmax][nmax],?n,?m;??
int?main(){??
????while(cin?>>?n?>>?m?&&?n!=?0){??
????????//構建鄰接矩陣??
????????int?i,?j;??
????????for(i?=?1;?i?<=?n;?i++){??
????????????for(j?=?1;?j?<=?n;?j++){??
????????????????edge[i][j]?=?inf;??
????????????}??
????????????edge[i][i]?=?0;??
????????}??
????????while(m--){??
????????????cin?>>?i?>>?j;??
????????????cin?>>?edge[i][j];??
????????????edge[j][i]?=?edge[i][j];??
????????}??
????????//使用弗洛伊德算法??
????????int?k;??
????????for(k?=?1;?k?<=?n;?k++){??
????????????for(i?=?1;?i?<=?n;?i++){??
????????????????for(j?=?1;?j?<=?n;?j++){??
????????????????????if(edge[i][k]?<?inf?&&?edge[k][j]?<?inf?&&?edge[i][j]?>?edge[i][k]?+?edge[k][j])??
????????????????????????edge[i][j]?=?edge[i][k]?+?edge[k][j];??
????????????????}??
????????????}??
????????}??
????????cout?<<?edge[1][n]?<<?endl;??
????}??
????return?0;??
}??

程序運行結果如下：

?

3），迪杰斯特拉算法（解決單源最短路徑）
基本思想：每次找到離源點（如1號結點）最近的一個頂點，然后以該頂點為中心進行擴展，最終得到源點到其余所有點的最短路徑。
基本步驟：1，設置標記數組book[]：將所有的頂點分為兩部分,已知最短路徑的頂點集合P和未知最短路徑的頂點集合Q，很顯然最開始集合P只有源點一個頂點。book[i]為1表示在集合P中；
2，設置最短路徑數組dst[]并不斷更新：初始狀態下，令dst[i] = edge[s][i](s為源點，edge為鄰接矩陣)，很顯然此時dst[s]=0，book[s]=1。此時，在集合Q中可選擇一個離源點s最近的頂點u加入到P中。并依據以u為新的中心點，對每一條邊進行松弛操作(松弛是指由結點s-->j的途中可以經過點u，并令dst[j]=min{dst[j], dst[u]+edge[u][j]})，并令book[u]=1;
3，在集合Q中再次選擇一個離源點s最近的頂點v加入到P中。并依據v為新的中心點，對每一條邊進行松弛操作(即dst[j]=min{dst[j], dst[v]+edge[v][j]}),并令book[v]=1;
4，重復3，直至集合Q為空。
以下是圖示：

核心代碼如下所示：

[cpp]?view plain?copy

#define?inf?99999999??
/***構建鄰接矩陣edge[][],且1為源點***/??
for(i?=?1;?i?<=?n;?i++)?dst[i]?=?edge[1][s]；??
for(i?=?1;?i?<=?n;?i++)?book[i]?=?0;??
book[1]?=?1;??
for(i?=?1;?i?<=?n-1;?i++){??
????//找到離源點最近的頂點u，稱它為新中心點??
????min?=?inf;??
????for(j?=?1;?j?<=?n;?j++){??
????????if(book[j]?==?0?&&?dst[j]?<?min){??
????????????min?=?dst[j];??
????????????u?=?j;??
????????}??
????}??
????book[u]?=?1;??
????//更新最短路徑數組??
????for(k?=?1;?k?<=?n;?k++){??
????????if(edge[u][k]?<?inf?&&?book[k]?==?0){??
????????????if(dst[k]?>?dst[u]?+?edge[u][k])??
????????????????dst[k]?=?dst[u]?+?edge[u][k];?????????????
????????}??
????}??
}??

例1：給你n個點，m條無向邊，每條邊都有長度d和花費p，給你起點s，終點t，要求輸出起點到終點的最短距離及其花費，如果最短距離有多條路線，則輸出花費最少的。
輸入：輸入n,m，點的編號是1~n,然后是m行，每行4個數 a,b,d,p，表示a和b之間有一條邊，且其長度為d，花費為p。最后一行是兩個數s,t;起點s，終點 t。n和m為 0 時輸入結束。(1<n<=1000, 0<m<100000, s != t)
輸出：輸出一行，有兩個數，最短距離及其花費。
分析：由于每條邊有長度d和花費p，最好構建邊結構體存放，此外可以使用鄰接鏈表，使用鄰接鏈表時需要將上面的核心代碼修改幾個地方：

1，初始化dst[]時使用結點1的鄰接鏈表；
2，更新最短路徑數組時，k的范圍由1~n變為1~edge[u].size()。先采用鄰接矩陣解決此題，再使用鄰接表解決此題，兩種方法的思路都一樣：初始化鄰接矩陣或鄰接鏈表，并
初始化最短路徑數組dst ----> n-1輪邊的松弛中，先找到離新源點最近的中心點u，之后根據中心點u為轉折點來更新路徑數組。

使用鄰接矩陣求解：

[cpp]?view plain?copy

/***對于無向圖，輸入n,m，點的編號是1~n,然后是m行，每行4個數?a,b,d,p，表示a和b之間有一條邊，且其長度為d，花費為p。最后一行是兩個數s,t;起點s，終點?t。***/??
/***n和m為?0?時輸入結束。(1<n<=1000,?0<m<100000,?s?!=?t)?????輸出：輸出一行，有兩個數，?最短距離及其花費。***/??
#include?<iostream>??
#include?<iomanip>??
using?namespace?std;??
#define?nmax?1001??
#define?inf?99999999??
struct?Edge{??
????int?len;??
????int?cost;??
};??
Edge?edge[nmax][nmax];??
int?dst[nmax],?spend[nmax],?book[nmax],?n,?m,?stNode,?enNode;??
int?main(){??
????while(cin?>>?n?>>?m?&&?n?!=?0?&&?m?!=?0){??
????????int?a,?b,?i,?j;??
????????//構建鄰接矩陣和最短路徑數組??
????????for(i?=?1;?i?<=?n;?i++){??
????????????for(j?=?1;?j?<=?n;?j++){??
????????????????edge[i][j].cost?=?0;??
????????????????edge[i][j].len?=?inf;??
????????????}??
????????????edge[i][i].len?=?0;??
????????}??
????????while(m--){??
????????????cin?>>?a?>>?b;??
????????????cin?>>?edge[a][b].len?>>?edge[a][b].cost;??
????????????edge[b][a].len?=?edge[a][b].len;??
????????????edge[b][a].cost?=?edge[a][b].cost;??
????????}??
????????cin?>>?stNode?>>?enNode;??
????????for(i?=?1;?i?<=?n;?i++){??
????????????dst[i]?=?edge[stNode][i].len;??
????????????spend[i]?=?edge[stNode][i].cost;??
????????}??
????????memset(book,?0,?sizeof(book));??
????????book[stNode]?=?1;??
????????//開始迪杰斯特拉算法，進行剩余n-1次松弛??
????????int?k;??
????????for(k?=?1;?k?<=?n-1;?k++){??
????????????//找離源點最近的頂點u??
????????????int?minNode,?min?=?inf;??
????????????for(i?=?1;?i?<=?n;?i++){??
????????????????if(book[i]?==?0?&&?min?>?dst[i]?/*?||?min?==?dst[i]&&?edge[stNode][min].cost?>?edge[stNode][i].cost*/){??
????????????????????min?=?dst[i];??
????????????????????minNode?=?i;??
????????????????}??
????????????}??
????????????//cout?<<?setw(2)?<<?minNode;??
????????????book[minNode]?=?1;//易錯點1，錯寫成book[i]=1??
????????????//以中心點u為轉折點來更新路徑數組和花費數組??
????????????for(i?=?1;?i?<=?n;?i++){??
????????????????if(book[i]?==?0?&&?dst[i]?>?dst[minNode]?+?edge[minNode][i].len?||?dst[i]?==?dst[minNode]?+?edge[minNode][i].len?&&?spend[i]?>?spend[minNode]?+?edge[minNode][i].cost){??
????????????????????dst[i]?=?dst[minNode]?+?edge[minNode][i].len;//易錯點2，錯寫成dst[i]+??
????????????????????spend[i]?=?spend[minNode]?+?edge[minNode][i].cost;??
????????????????}??
????????????}??
????????}??
????????cout?<<?dst[enNode]?<<?setw(3)?<<?spend[enNode]?<<?endl;??
????}??
????return?0;??
}??

程序運行結果如下：

使用鄰接鏈表求解：

[cpp]?view plain?copy

/***對于無向圖，輸入n,m，點的編號是1~n,然后是m行，每行4個數?a,b,d,p，表示a和b之間有一條邊，且其長度為d，花費為p。最后一行是兩個數s,t;起點s，終點?t。***/??
/***n和m為?0?時輸入結束。(1<n<=1000,?0<m<100000,?s?!=?t)?????輸出：輸出一行，有兩個數，?最短距離及其花費。***/??
#include?<iostream>??
#include?<iomanip>??
#include?<vector>??
using?namespace?std;??
#define?nmax?1001??
#define?inf?99999999??
struct?Edge{??
????int?len;??
????int?cost;??
????int?next;??
};??
vector<Edge>?edge[nmax];??
int?dst[nmax],?spend[nmax],?book[nmax],?n,?m,?stNode,?enNode;??
int?main(){??
????while(cin?>>?n?>>?m?&&?n?!=?0?&&?m?!=?0){??
????????int?a,?b,?i,?j;??
????????//構建鄰接表和最短路徑數組??
????????for(i?=?1;?i?<=?n;?i++)?edge[i].clear();??
????????while(m--){??
????????????Edge?tmp;??
????????????cin?>>?a?>>?b;??
????????????tmp.next?=?b;??
????????????cin?>>?tmp.len?>>?tmp.cost;??
????????????edge[a].push_back(tmp);??
????????????tmp.next?=?a;??
????????????edge[b].push_back(tmp);??
????????}??
????????cin?>>?stNode?>>?enNode;??
????????for(i?=?1;?i?<=?n;?i++)?dst[i]?=?inf;?//注意2，別忘記寫此句來初始化dst[]??
????????for(i?=?0;?i?<?edge[stNode].size();?i++){//注意1，從下標0開始存元素，誤寫成i?<=?edge[stNode].size()??
????????????dst[edge[stNode][i].next]?=?edge[stNode][i].len;??
????????????//cout?<<?dst[2]?<<?endl;??
????????????spend[edge[stNode][i].next]?=?edge[stNode][i].cost;??
????????}??
????????memset(book,?0,?sizeof(book));??
????????book[stNode]?=?1;??
????????//開始迪杰斯特拉算法，進行剩余n-1次松弛??
????????int?k;??
????????for(k?=?1;?k?<=?n-1;?k++){??
????????????//找離源點最近的頂點u??
????????????int?minnode,?min?=?inf;??
????????????for(i?=?1;?i?<=?n;?i++){??
????????????????if(book[i]?==?0?&&?min?>?dst[i]?/*?||?min?==?dst[i]&&?edge[stnode][min].cost?>?edge[stnode][i].cost*/){??
????????????????????min?=?dst[i];??
????????????????????minnode?=?i;??
????????????????}??
????????????}??
????????????//cout?<<?setw(2)?<<?minnode;??
????????????book[minnode]?=?1;//易錯點1，錯寫成book[i]=1??
????????????//以中心點u為轉折點來更新路徑數組和花費數組??
????????????for(i?=?0;?i?<?edge[minnode].size();?i++){??
????????????????int?t?=?edge[minnode][i].next;//別忘了加此句，表示與結點minnode相鄰的點??
????????????????if(book[t]?==?0?&&?dst[t]?>?dst[minnode]?+?edge[minnode][i].len?||?dst[t]?==?dst[minnode]?+?edge[minnode][i].len?&&?spend[t]?>?spend[minnode]?+?edge[minnode][i].cost){??
????????????????????dst[t]?=?dst[minnode]?+?edge[minnode][i].len;??
????????????????????spend[t]?=?spend[minnode]?+?edge[minnode][i].cost;??
????????????????}??
????????????}??
????????}??
????????cout?<<?dst[enNode]?<<?setw(3)?<<?spend[enNode]?<<?endl;??
????}??
????return?0;??
}??

程序運行結果如下：

使用鄰接表時，注意更新dst[]，book[]時要使用鄰接表元素對應下標中的next成員，而涉及到權值加減時時需要使用鄰接表中的對應下標來取得權值；而使用鄰接矩陣就沒這么多顧慮了，因為這時候鄰接矩陣對應下標和dst[]要更新元素的下標正好一致，都是從1開始編號。

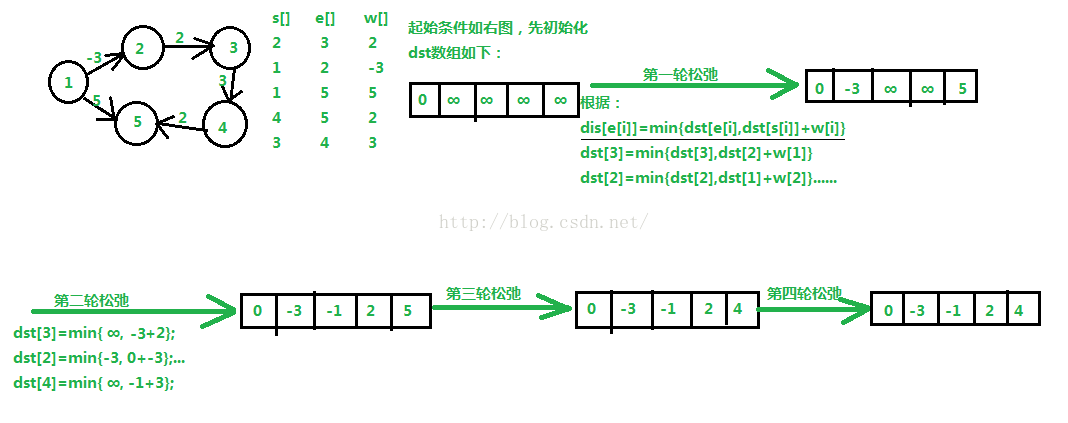
4），Bellman-Ford算法(解決負權邊，解決單源最短路徑，前幾種方法不能求含負權邊的圖)：：時間復雜度O(nm),空間復雜度O(m)
主要思想：對所有的邊進行n-1輪松弛操作，因為在一個含有n個頂點的圖中，任意兩點之間的最短路徑最多包含n-1邊。換句話說，第1輪在對所有的邊進行松弛后，得到的是從1號頂點只能經過一條邊到達其余各定點的最短路徑長度。第2輪在對所有的邊進行松弛后，得到的是從1號頂點只能經過兩條邊到達其余各定點的最短路徑長度，......
以下是圖示：