Binary cross entropy 二元交叉熵是二分類問題中常用的一個Loss損失函數，在常見的機器學習模塊中都有實現。本文就二元交叉熵這個損失函數的原理，簡單地進行解釋。

首先是二元交叉熵的公式 :
$$Loss=?\frac{1}{N}\sum _{i=1}^N{y}_i?\log (p(y_i))+(1?y_i)?log(1?p(y_i))$$

其中，$y$ 是二元標簽 0 或者 1， $p(y)$ 是輸出屬于$y$ 標簽的概率。作為損失函數，二元交叉熵是用來評判一個二分類模型預測結果的好壞程度的，通俗的講，即對于標簽y為1的情況，如果預測值p(y)趨近于1，那么損失函數的值應當趨近于0。反之，如果此時預測值p(y)趨近于0，那么損失函數的值應當非常大，這非常符合log函數的性質。

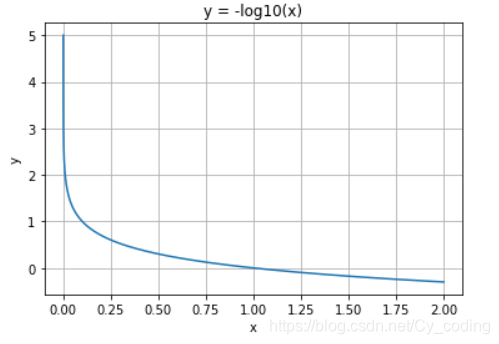
下面以單個輸出為例子，在標簽為 $y=1$ 的情況下$Loss=?\log (p(y))$, 當預測值接近1時，$Loss=0$， 反之 $Loss$ 趨向于正無窮。

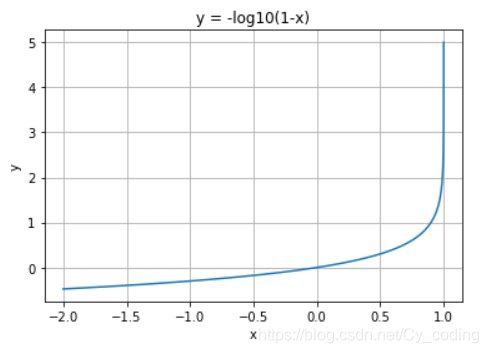
同樣的單個輸出為例，當標簽 $y=0$時，損失函數 $Loss=?\log (1?p(y))$，當預測值接近0時，$Loss=0$，反之$Loss$ 趨向于正無窮。

之后，再對所有計算出的單個輸出損失求和求平均，就可以求出模型針對一組大小為N的輸出的Loss了。