在之前，我總結了關于計算機神經網絡與梯度下降的核心，詳見下文鏈接 :
一文看懂計算機神經網絡與梯度下降
本文主要會對圖像相關的機器學習中最為重要的網絡，卷積神經網絡作個人的理解分析。

1. 為什么要使用卷積神經網絡

在講述原理之前，我們先來解釋為什么我們在圖像及視頻等等領域的機器學習中要使用CNN。我們都知道，使用多層感知器，有隱藏層的深度神經網絡可以幫助我們解決分類，聚合，回歸問題。但當我們的輸入輸出轉變為高維度的數據，例如圖片時，不可避免地要面臨神經元過多，參數量過大的問題。假設我們使用一張720*480的圖片作為輸入，一張圖片對應的參數量就已經達到了345600個，如果我們單純地將數據壓為一維向量并繼續使用全連接的神經網絡，那不可避免的會極大增加運算成本，降低模型的效率，顯然是不科學的。同樣的，對于圖像而言，如果說像素點的灰度值或RGB值可以對應我們在一維數據中使用的數值，那么圖像的空間性在我們將其轉變為一維后實際上是被拋棄了，這會導致我們忽略了圖像局部形態所包含的信息，使得一些非常輕微的平移旋轉對結果產生翻天覆地的變化，這是我們不能容忍的。對于我們來說，兩個圖片中不同位置的物體所包含的含義應當是一致的，即只應當考慮圖片的相對位置而非絕對位置。
在接下來的部分，我會著重闡述卷積神經網絡的原理，其中包含一些個人的看法理解。

2. 圖像處理中的卷積核

要想理解卷積神經網絡的運作，首先必須理解圖像處理中卷積的含義。需要注意的是，雖然卷積神經網絡中有卷積二字，但是其實他與傳統意義上數學定義的卷積是有區別的。更為準確的叫法應當稱之為協相關神經網絡，而非卷積神經網絡。如下圖所示，我們以一個常見的3*3的卷積核為例，目標像素點對應的值由其周圍對應的原像素點和卷積核計算協相關得來。

由上圖我們不難發現，經過卷積后的目標圖像中的每一個像素點都對應了原圖像中的局部特征，使用不同的卷積核，就可以從原圖像中提取出不一樣的局部特征了。計算目標圖像的方式，是將卷積核在原圖像上滑動，與各個部分的圖像分別計算卷積直到遍歷全部的原圖像。
$$h^n(i,j)=(h^{n?1}?{\omega }_k)(i,j)=\sum _{n=?\frac{d?1}{2}}^{\frac{d?1}{2}}\sum _{m=?\frac{d?1}{2}}^{\frac{d?1}{2}}{h}^{n?1}(i+n,j+m)?\omega (n,m)$$
上式就是圖像處理中使用卷積核進行卷積運算的數學定義，其中 $h^n$ 是計算得出的目標圖像，$h^{n?1}$ 對應原圖像， $\omega$ 就是用于計算的卷積核， $d$ 是卷積核的大小。

更多有關圖像處理中卷積的基礎，可以參考以下鏈接中的文章 :
數字圖像處理中濾波和卷積操作詳細說明

3. 卷積神經網絡原理

在理解了卷積神經網絡中"卷積"的運算方式，我們接下來就來看看卷積神經網絡的計算原理。輸入輸出的維度在理解卷積神經網絡的過程中至關重要。

我們日常生活中常處理的圖像按照他們的通道區分往往可以分為兩大類，單通道的灰度圖像以及三通道的RGB圖像。下圖就給出了一個針對三通道RGB圖像的單層卷積神經網絡的運算，我們就以下圖為例，來理解卷積神經網絡中隱藏層各個神經元以及權重的計算。首先，輸入是$28?28?3$的RGB圖，其中3分別代表RGB三個通道。我們這里只使用了一個$5?5$的卷積核。我們對每一個通道分別計算卷積，并將結果相加，就得到了一個包含$24?24$個神經元的隱藏層。需要注意的是，每一個得出的隱藏層都共用一個卷積核中的權重，例如下圖中，隱藏層$h_1^n$ 共用同一個權重矩陣(卷積核) ${\omega }_1^n$。通過這樣的操作，我們就提取出了由這個卷積核描述的特征。

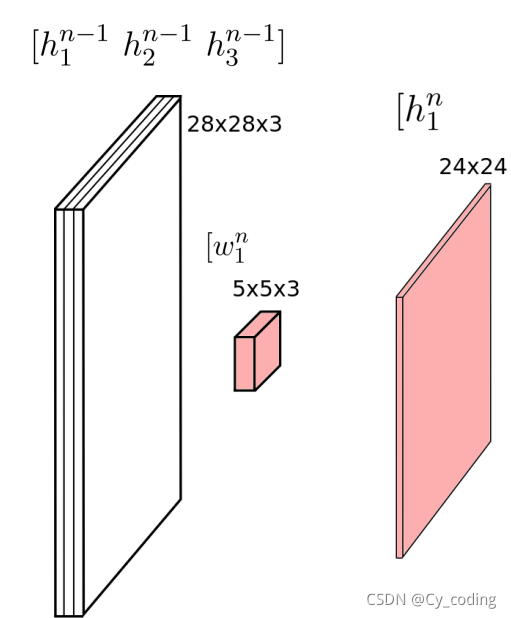
接著，如果我們使用不止一個卷積核，那顯而易見的，就可以提取出圖像中不同的特征了。因此，計算得出的隱藏層的層數，與選擇使用的卷積核的個數是一致的。

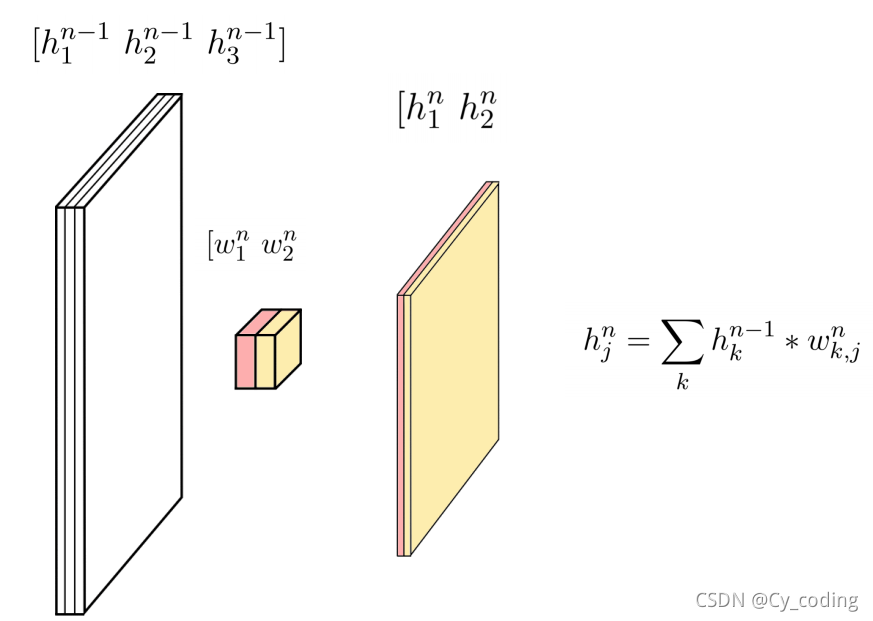
綜上所述，我們可以通過不同的卷積核來提取出圖像中的不同特征。而我們使用卷積神經網絡的過程，實際上是通過訓練來確定各個卷積核的權重，從而提取出最適合的圖像特征。使用不同長度大小的卷積核，在訓練卷積神經網絡的過程中，可以幫助我們提取出最優的特征來組成feature maps。之后再結合全連接神經網絡來完成相關的圖像分類聚合問題。