1 問題
之前我們考慮的訓練數據中樣例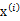 的個數m都遠遠大于其特征個數n,這樣不管是進行回歸、聚類等都沒有太大的問題。然而當訓練樣例個數m太小,甚至m<
的個數m都遠遠大于其特征個數n,這樣不管是進行回歸、聚類等都沒有太大的問題。然而當訓練樣例個數m太小,甚至m<
多元高斯分布的參數估計公式如下:
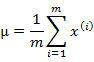
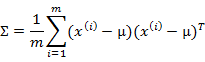
分別是求mean和協方差的公式,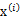 表示樣例,共有m個,每個樣例n個特征,因此
表示樣例,共有m個,每個樣例n個特征,因此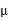 是n維向量,
是n維向量,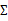 是n*n協方差矩陣。
是n*n協方差矩陣。
當m<是奇異陣(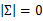 ),也就是說
),也就是說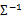 不存在,沒辦法擬合出多元高斯分布了,確切的說是我們估計不出來
不存在,沒辦法擬合出多元高斯分布了,確切的說是我們估計不出來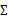 。
。
如果我們仍然想用多元高斯分布來估計樣本,那怎么辦呢?
2 限制協方差矩陣
當沒有足夠的數據去估計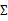 時,那么只能對模型參數進行一定假設,之前我們想估計出完全的
時,那么只能對模型參數進行一定假設,之前我們想估計出完全的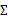 (矩陣中的全部元素),現在我們假設
(矩陣中的全部元素),現在我們假設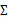 就是對角陣(各特征間相互獨立),那么我們只需要計算每個特征的方差即可,最后的
就是對角陣(各特征間相互獨立),那么我們只需要計算每個特征的方差即可,最后的 只有對角線上的元素不為0
只有對角線上的元素不為0
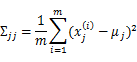
回想我們之前討論過的二維多元高斯分布的幾何特性,在平面上的投影是個橢圓,中心點由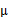 決定,橢圓的形狀由
決定,橢圓的形狀由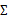 決定。
決定。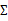 如果變成對角陣,就意味著橢圓的兩個軸都和坐標軸平行了。
如果變成對角陣,就意味著橢圓的兩個軸都和坐標軸平行了。
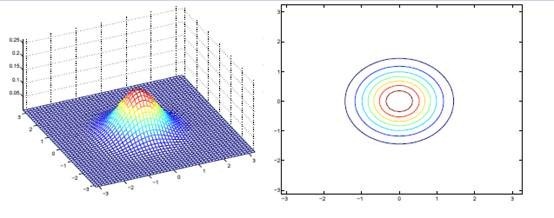
如果我們想對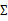 進一步限制的話,可以假設對角線上的元素都是等值的。
進一步限制的話,可以假設對角線上的元素都是等值的。
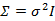
其中
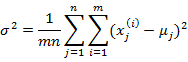
也就是上一步對角線上元素的均值,反映到二維高斯分布圖上就是橢圓變成圓。
當我們要估計出完整的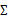 時,我們需要m>=n+1才能保證在最大似然估計下得出的
時,我們需要m>=n+1才能保證在最大似然估計下得出的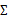 是非奇異的。然而在上面的任何一種假設限定條件下,只要m>=2都可以估計出限定的
是非奇異的。然而在上面的任何一種假設限定條件下,只要m>=2都可以估計出限定的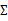 。
。
這樣做的缺點也是顯然易見的,我們認為特征間獨立,這個假設太強。接下來,我們給出一種稱為因子分析的方法,使用更多的參數來分析特征間的關系,并且不需要計算一個完整的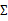 。
。
3 邊緣和條件高斯分布
在討論因子分析之前,先看看多元高斯分布中,條件和邊緣高斯分布的求法。這個在后面因子分析的EM推導中有用。
假設x是有兩個隨機向量組成(可以看作是將之前的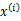 分成了兩部分)
分成了兩部分)
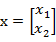
其中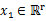 ,
,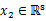 ,那么
,那么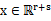 。假設x服從多元高斯分布
。假設x服從多元高斯分布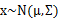 ,其中
,其中
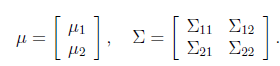
其中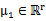 ,
,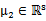 ,那么
,那么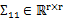 ,
,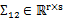 ,由于協方差矩陣是對稱陣,因此
,由于協方差矩陣是對稱陣,因此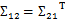 。
。
整體看來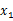 和
和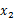 聯合分布符合多元高斯分布。
聯合分布符合多元高斯分布。
那么只知道聯合分布的情況下,如何求得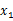 的邊緣分布呢?從上面的
的邊緣分布呢?從上面的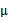 和
和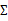 可以看出,
可以看出,
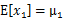 ,
,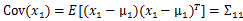 ,下面我們驗證第二個結果
,下面我們驗證第二個結果
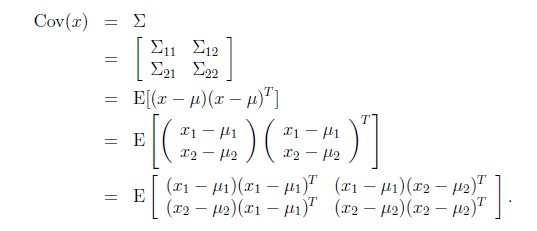
由此可見,多元高斯分布的邊緣分布仍然是多元高斯分布。也就是說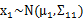 。
。
上面Cov(x)里面有趣的是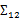 ,這個與之前計算協方差的效果不同。之前的協方差矩陣都是針對一個隨機變量(多維向量)來說的,而
,這個與之前計算協方差的效果不同。之前的協方差矩陣都是針對一個隨機變量(多維向量)來說的,而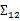 評價的是兩個隨機向量之間的關系。比如
評價的是兩個隨機向量之間的關系。比如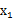 ={身高,體重},
={身高,體重},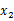 ={性別,收入},那么
={性別,收入},那么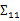 求的是身高與身高,身高與體重,體重與體重的協方差。而
求的是身高與身高,身高與體重,體重與體重的協方差。而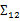 求的是身高與性別,身高與收入,體重與性別,體重與收入的協方差,看起來與之前的大不一樣,比較詭異的求法。
求的是身高與性別,身高與收入,體重與性別,體重與收入的協方差,看起來與之前的大不一樣,比較詭異的求法。
上面求的是邊緣分布,讓我們考慮一下條件分布的問題,也就是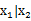 的問題。根據多元高斯分布的定義,
的問題。根據多元高斯分布的定義,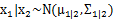 。
。
且
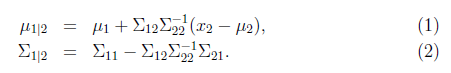
這是我們接下來計算時需要的公式,這兩個公式直接給出,沒有推導過程。如果想了解具體的推導過程,可以參見Chuong B. Do寫的《Gaussian processes》。
4 因子分析例子
下面通過一個簡單例子,來引出因子分析背后的思想。
因子分析的實質是認為m個n維特征的訓練樣例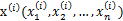 的產生過程如下:
的產生過程如下:
1、 首先在一個k維的空間中按照多元高斯分布生成m個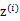 (k維向量),即
(k維向量),即
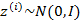
2、 然后存在一個變換矩陣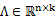 ,將
,將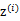 映射到n維空間中,即
映射到n維空間中,即
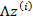
因為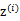 的均值是0,映射后仍然是0。
的均值是0,映射后仍然是0。
3、 然后將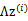 加上一個均值
加上一個均值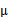 (n維),即
(n維),即
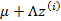
對應的意義是將變換后的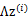 (n維向量)移動到樣本
(n維向量)移動到樣本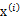 的中心點
的中心點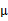 。
。
4、 由于真實樣例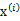 與上述模型生成的有誤差,因此我們繼續加上誤差
與上述模型生成的有誤差,因此我們繼續加上誤差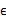 (n維向量),
(n維向量),
而且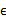 符合多元高斯分布,即
符合多元高斯分布,即
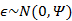
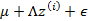
5、 最后的結果認為是真實的訓練樣例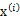 的生成公式
的生成公式
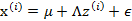
讓我們使用一種直觀方法來解釋上述過程:
假設我們有m=5個2維的樣本點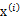 (兩個特征),如下:
(兩個特征),如下:
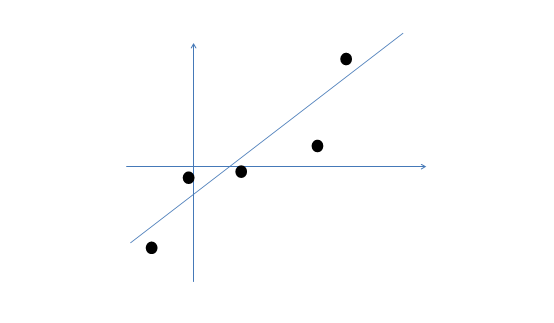
那么按照因子分析的理解,樣本點的生成過程如下:
1、 我們首先認為在1維空間(這里k=1),存在著按正態分布生成的m個點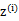 ,如下
,如下
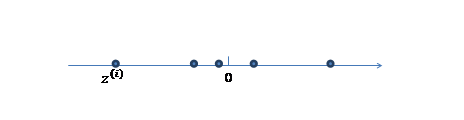
均值為0,方差為1。
2、 然后使用某個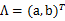 將一維的z映射到2維,圖形表示如下:
將一維的z映射到2維,圖形表示如下:
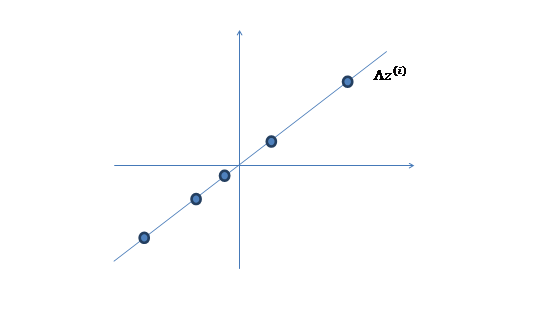
3、 之后加上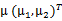 ,即將所有點的橫坐標移動
,即將所有點的橫坐標移動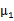 ,縱坐標移動
,縱坐標移動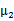 ,將直線移到一個位置,使得直線過點
,將直線移到一個位置,使得直線過點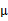 ,原始左邊軸的原點現在為
,原始左邊軸的原點現在為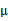 (紅色點)。
(紅色點)。
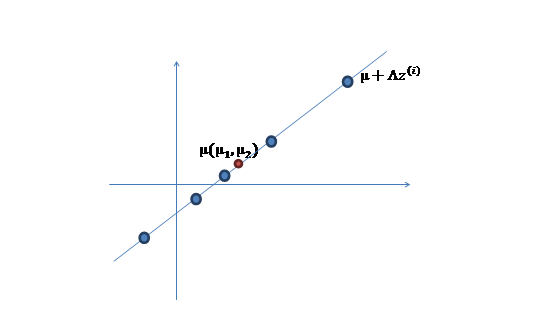
然而,樣本點不可能這么規則,在模型上會有一定偏差,因此我們需要將上步生成的點做一些擾動(誤差),擾動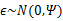 。
。
4、 加入擾動后,我們得到黑色樣本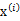 如下:
如下:
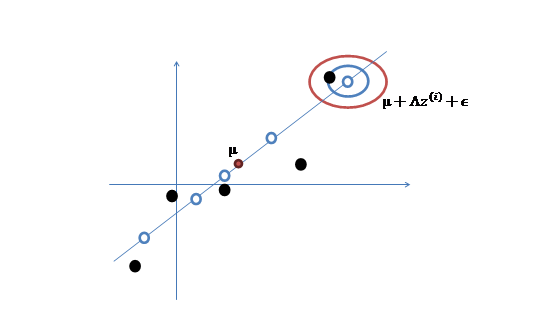
5、 其中由于z和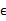 的均值都為0,因此
的均值都為0,因此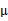 也是原始樣本點(黑色點)的均值。
也是原始樣本點(黑色點)的均值。
由以上的直觀分析,我們知道了因子分析其實就是認為高維樣本點實際上是由低維樣本點經過高斯分布、線性變換、誤差擾動生成的,因此高維數據可以使用低維來表示。
5 因子分析模型
上面的過程是從隱含隨機變量z經過變換和誤差擾動來得到觀測到的樣本點。其中z被稱為因子,是低維的。
我們將式子再列一遍如下:
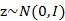
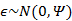
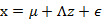
其中誤差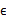 和z是獨立的。
和z是獨立的。
下面使用的因子分析表示方法是矩陣表示法,在參考資料中給出了一些其他的表示方法,如果不明白矩陣表示法,可以參考其他資料。
矩陣表示法認為z和x聯合符合多元高斯分布,如下
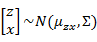
求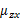 之前需要求E[x]
之前需要求E[x]
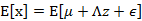
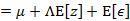
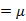
我們已知E[z]=0,因此
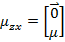
下一步是計算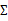 ,
,
其中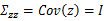
接著求
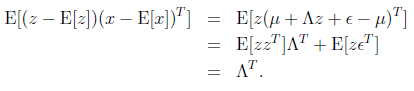
這個過程中利用了z和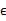 獨立假設(
獨立假設(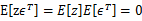 )。并將
)。并將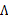 看作已知變量。
看作已知變量。
接著求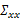
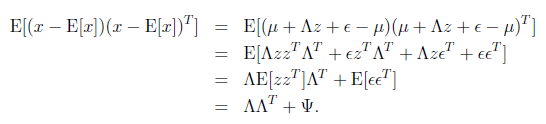
然后得出聯合分布的最終形式
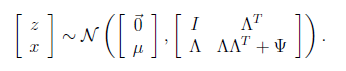
從上式中可以看出x的邊緣分布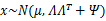
那么對樣本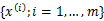 進行最大似然估計
進行最大似然估計
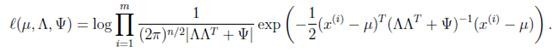
然后對各個參數求偏導數不就得到各個參數的值了么?
可惜我們得不到closed-form。想想也是,如果能得到,還干嘛將z和x放在一起求聯合分布呢。根據之前對參數估計的理解,在有隱含變量z時,我們可以考慮使用EM來進行估計。
6 因子分析的EM估計
我們先來明確一下各個參數,z是隱含變量,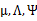 是待估參數。
是待估參數。
回想EM兩個步驟:
循環重復直到收斂 {
(E步)對于每一個i,計算
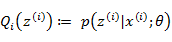
(M步)計算
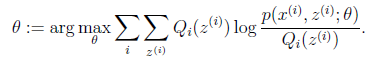
我們套用一下:
(E步):
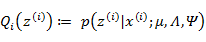
根據第3節的條件分布討論,
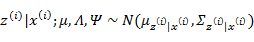
因此
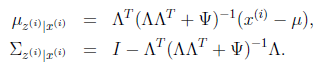
那么根據多元高斯分布公式,得到
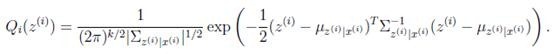
(M步):
直接寫要最大化的目標是
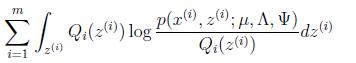
其中待估參數是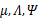
下面我們重點求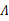 的估計公式
的估計公式
首先將上式簡化為:
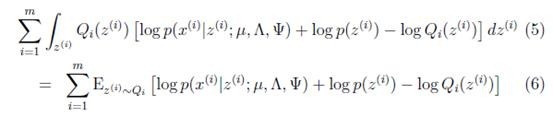
這里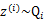 表示
表示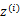 服從
服從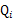 分布。然后去掉與
分布。然后去掉與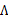 不相關的項(后兩項),得
不相關的項(后兩項),得
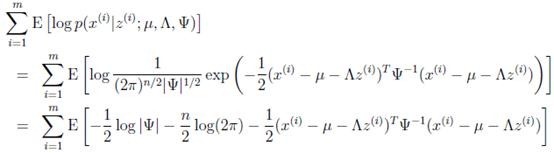
去掉不相關的前兩項后,對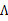 進行導,
進行導,
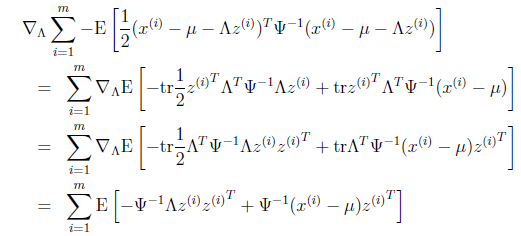
第一步到第二步利用了tr a = a(a是實數時)和tr AB = tr BA。最后一步利用了
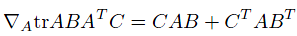
tr就是求一個矩陣對角線上元素和。
最后讓其值為0,并且化簡得
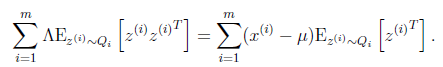
然后得到
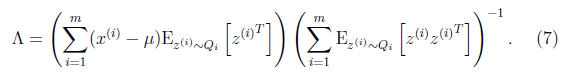
到這里我們發現,這個公式有點眼熟,與之前回歸中的最小二乘法矩陣形式類似
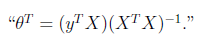
這里解釋一下兩者的相似性,我們這里的x是z的線性函數(包含了一定的噪聲)。在E步得到z的估計后,我們找尋的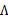 實際上是x和z的線性關系。而最小二乘法也是去找特征和結果直接的線性關系。
實際上是x和z的線性關系。而最小二乘法也是去找特征和結果直接的線性關系。
到這還沒完,我們需要求得括號里面的值
根據我們之前對z|x的定義,我們知道
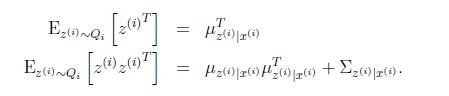
第一步根據z的條件分布得到,第二步根據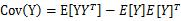 得到
得到
將上面的結果代入(7)中得到
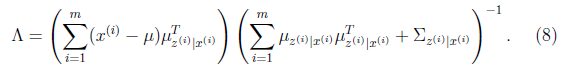
至此,我們得到了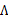 ,注意一點是E[z]和
,注意一點是E[z]和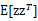 的不同,后者需要求z的協方差。
的不同,后者需要求z的協方差。
其他參數的迭代公式如下:
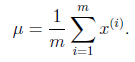
均值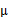 在迭代過程中值不變。
在迭代過程中值不變。

然后將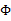 上的對角線上元素抽取出來放到對應的
上的對角線上元素抽取出來放到對應的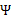 中,就得到了
中,就得到了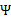 。
。
7 總結
根據上面的EM的過程,要對樣本X進行因子分析,只需知道要分解的因子數(z的維度)即可。通過EM,我們能夠得到轉換矩陣 和誤差協方差
和誤差協方差 。
。
因子分析實際上是降維,在得到各個參數后,可以求得z。但是z的各個參數含義需要自己去琢磨。
下面從一個ppt中摘抄幾段話來進一步解釋因子分析。
因子分析(factor analysis)是一種數據簡化的技術。它通過研究眾多變量之間的內部依賴關系,探求觀測數據中的基本結構,并用少數幾個假想變量來表示其基本的數據結構。這幾個假想變量能夠反映原來眾多變量的主要信息。原始的變量是可觀測的顯在變量,而假想變量是不可觀測的潛在變量,稱為因子。
例如,在企業形象或品牌形象的研究中,消費者可以通過一個有24個指標構成的評價體系,評價百貨商場的24個方面的優劣。
但消費者主要關心的是三個方面,即商店的環境、商店的服務和商品的價格。因子分析方法可以通過24個變量,找出反映商店環境、商店服務水平和商品價格的三個潛在的因子,對商店進行綜合評價。而這三個公共因子可以表示為:
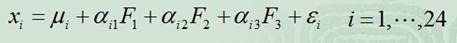
這里的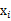 就是樣例x的第i個分量,
就是樣例x的第i個分量,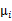 就是
就是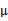 的第i個分量,
的第i個分量,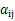 就是
就是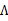 的第i行第j列元素,
的第i行第j列元素,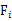 是z的第i個分量,
是z的第i個分量,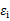 是
是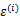 。
。
稱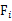 是不可觀測的潛在因子。24個變量共享這三個因子,但是每個變量又有自己的個性,不被包含的部分
是不可觀測的潛在因子。24個變量共享這三個因子,但是每個變量又有自己的個性,不被包含的部分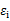 ,稱為特殊因子。
,稱為特殊因子。
注:
因子分析與回歸分析不同,因子分析中的因子是一個比較抽象的概念,而回歸因子有非常明確的實際意義;
主成分分析分析與因子分析也有不同,主成分分析僅僅是變量變換,而因子分析需要構造因子模型。
主成分分析:原始變量的線性組合表示新的綜合變量,即主成分;
因子分析:潛在的假想變量和隨機影響變量的線性組合表示原始變量。
PPT地址
其他值得參考的文獻
An Introduction to Probabilistic Graphical Models by Jordan Chapter 14



















