什么是算法?
人生皆算法，算法的本質，是解決問題的方法，遇到問題，尋找答案，解決問題，是作為一個人，一生都在做的事情。
算法是人類思維的產物，是解決問題的方案，并且，它能夠映射到計算機世界去實現，完成一些人類不擅長的事情，比如大量重復的計算。
算法很有魅力，它很特別，但是并不神秘，我們時時刻刻都在運用著算法背后的“解決問題”的思想去生活，去過著每一天。
用計算機思維去思考問題
算法是普通的，也是特別的，它是人類使用計算機思維思考的產物，能夠讓人類更加充分地利用計算機這個人類發明的工具，這也是信息時代特有的產物。
既然是計算機思維，當然有其特點：
概念不重要，理解即可，不必記憶，不必急于掌握，直接看實例體會。
“玩具”問題
計數：判斷一個byte（無符號整數）里面有多少個bit的值是1
算法一
很簡單的想法，將十進制數轉換為一位一位的二進制，然后看看是不是1就好了，就是簡單的數數。
// method 1
int cal_1(unsigned char number) {unsigned char count = 0;while (number != 0){int div = number % 2;if (div == 1) {count++;}number /= 2;}return count;
}
算法二
上面是我們解決問題的第一種想法。
下面我們加一種假設，假如內存空間足夠大，且使用函數次數足夠多，我們是不是可以提高算法的效率？
要知道，1字節大小的無符號整數，一共28 = 256種，如果我們連續10000次調用函數，每一次都使用除二取余法（算法1），就大量重復計算了，這個時候不妨提前算好把結果存起來，然后直接訪問結果（就像緩存、cache那樣的思想）。
也就是所謂的打表查表
// 計數：判斷一個byte（無符號整數）里面有多少個bit的值是1
#include <iostream>
using namespace std;int num_table[256] = { 0 };// method 1
int cal_1(unsigned char number) {unsigned char count = 0;while (number != 0){int div = number % 2;if (div == 1) {count++;}number /= 2;}return count;
}// method 2
int cal_2(unsigned char number) {return num_table[number];
}int main(){// 存儲答案for (unsigned char i = 0; i < 255; i++) {num_table[(int)i] = cal_1(i);}// 直接訪問cout << cal_2(15);return 0;
}
我們開始使用算法1，存儲了一張表，之后再需要使用的時候，就能夠直接查表得結果，而不需要再重復計算了，如果調用100000萬次，效率將會比算法1顯著提高。
當然……由于數據量對計算機來說太小了還是，測試不出很大的差異其實。
如果規模更大，會有顯著效果。
算法三
對于算法一
- 省空間，因為沒占用多少數據段
對于算法二 - 省時間，因為提前儲存好了答案，只需要訪問數組就可以
對于前面兩種算法，是根據不同需求不同情況取使用的，但是涉及到了算法設計考慮的兩個維度：時間和空間。
算法一省空間，費時間，算法二省時間廢空間，那么能不能兼得？
其實這種
不走極端取中間的兼得思想
在計算機中經常需要用到。
我們需要既省時間又省空間的算法。
與cache類似的設計思想
我們可以使用哈希表，采取如下策略
- 如果表中有值，那就直接取
- 如果沒有，就去計算，并且存表中
這樣一來，做到了拿走需要的，保存需要的，同時考慮了時間和空間兩方面的因素。
我們使用unordered_map完成這件事：
// 計數：判斷一個byte（無符號整數）里面有多少個bit的值是1
#include <iostream>
#include <unordered_map>
using namespace std;typedef std::unordered_map<unsigned char, int> result_map;// method three
int cal_3(unsigned char number, result_map &map) {result_map::iterator count = map.find(number);if (count != map.end()) // 在無序映射表中{cout << "在表中 ";return count->second;}else // 不在表中{cout << "不在表中 ";int result = cal_1(number);map.insert(result_map::value_type(number,result)); // 插入鍵值對return result;}}int main(){result_map map;cout << cal_3(15, map) << endl; // 不在表中 4cout << cal_3(15, map) << endl; // 在表中 4cout << cal_3(10, map) << endl; // 不在表中 2cout << cal_3(10, map) << endl; // 在表中 2return 0;
}
這樣，通過無序映射表，我們就完成了既節省時間，又節省空間的目的。
小結
我們來回顧一下。
對于這個問題
- 我們看到了問題，理解了問題
- 拆解問題，變成自己熟悉的
- 解決問題，創建解決問題的過程方案
- 設計解決流程，將其代碼實現
- 根據實際情況，優化解決方案
- 綜合考慮算法的時間和空間兩個維度的指標
我們通過這個超級簡單的例子，初步了解了算法的基本情況，我們繼續往下進行。
連續子序列和
讓我們體會一下不同的算法，不同的解決方案，感受一下它們之間的時間和空間上的性能差異。
一件事情，往往都是很多種解決方案，并且都能到達彼岸，但是過程不一樣，走過的路不同，花的時間也不同，算法的時空性能也是一樣的。
充分體會： 計算機世界是人類世界的二進制映射，與人類生活息息相關。
算法1：三層循環
- 取某個首位置
i - 取
i后的某個位置j - 計算
[i,j]數值的和，與最大值比較，更新最大值
這是一種最樸素的思想了，我們看圖。
因此，我們需要
for(int i = 0; i < char_size; i++){for(int j = i; j < char_size; j++){1. 求和2. 更新maxValue}
}
代碼如下：
#include <iostream>
#include <vector>
using namespace std;int max_subsequence_sum(const vector<int> &a) {int max_sum = 0;for (int i = 0; i < a.size(); i++) {for (int j = i; j < a.size(); j++) {int current_sum = 0;for (int k = i; k <= j; k++)current_sum += a[k];if (current_sum > max_sum)max_sum = current_sum;}}return max_sum;
}int main()
{vector<int> a = { 1,3,-1,2 };cout << max_subsequence_sum(a);return 0;
}
但是，毫無疑問，三重循環，時間消耗過多了，我們得看看能不能優化。
將三重循環轉換為遞歸。
代碼暫不寫
算法2：兩層循環
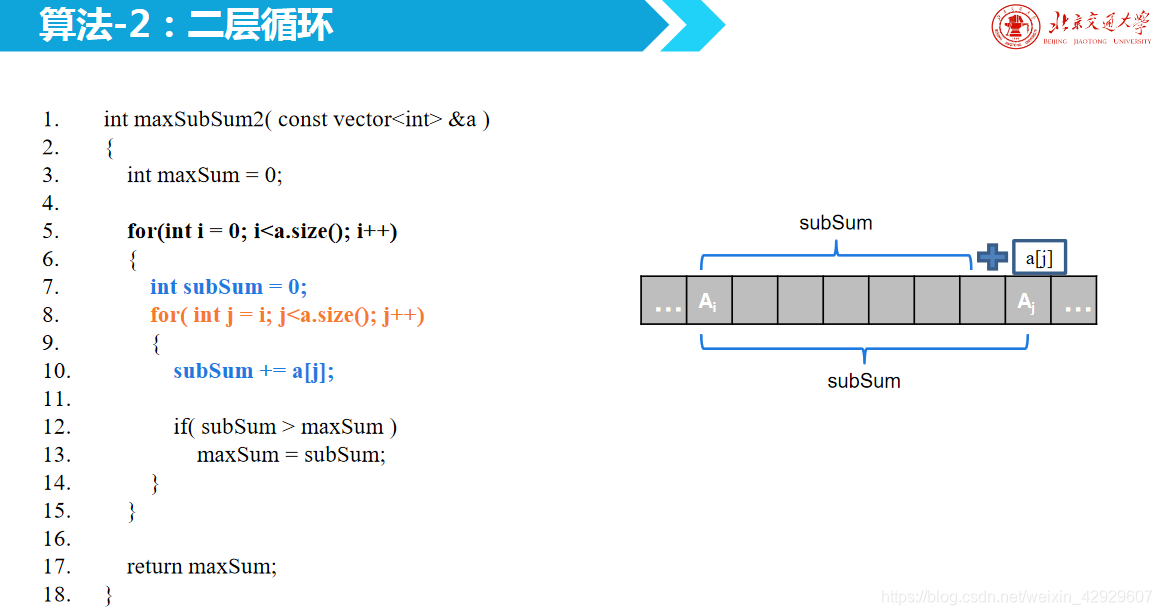
算法3：一層循環
算法4：遞歸
算法比較
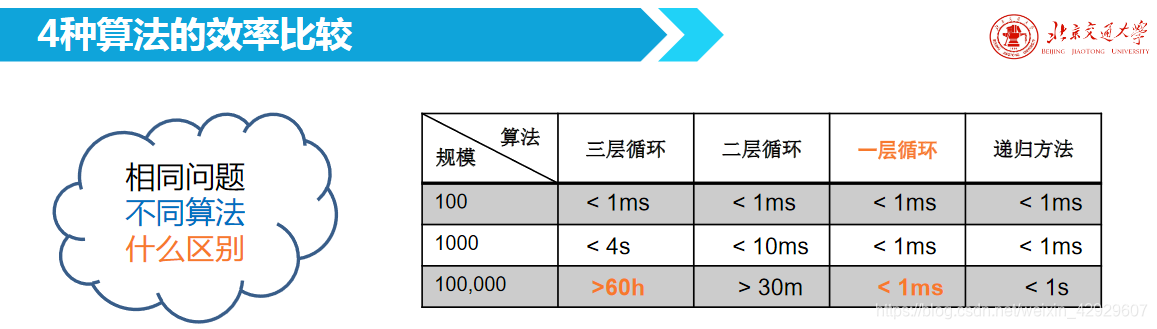
小結
之所以沒有談及后面的代碼，因為對于初學者來說比較復雜，看看就行了，充分體會的是同一個問題，達成同一個目的的情況下，不同算法的差異巨大，這也是算法魅力所在。
致謝
感謝北交大算法MOOC！
