分治思想，分治策略，自古有之，與人類生活息息相關，其本質是將大問題拆解為小問題，小問題轉換為已知解的問題，進而求解。

軍隊管理，國家分級治理……

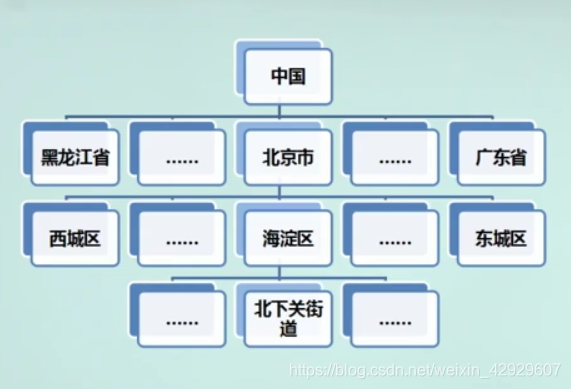
大規模數據排序，例如10000000000萬個數，規模大的時候，分治思想就很重要了。

基本思想

分！如果問題還大，就再分！直到其變成容易求解的基本問題，這個過程其實與遞歸的類似的。

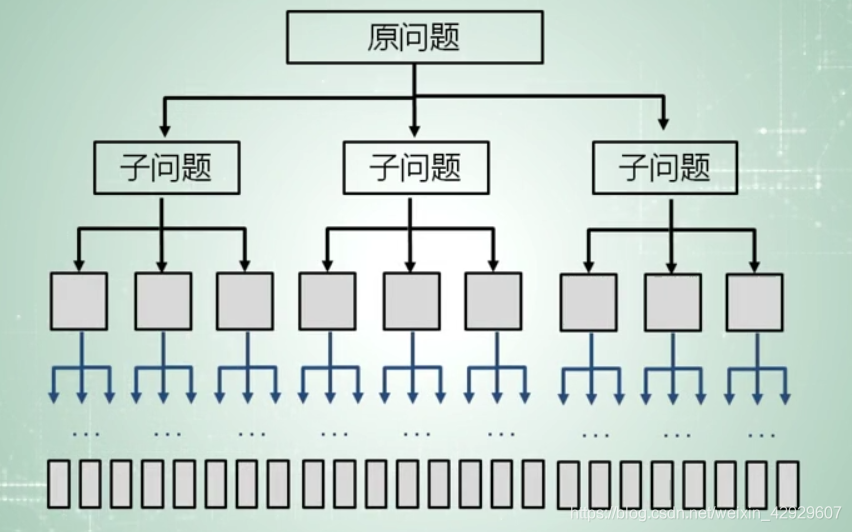
總而言之，遞歸思想與分治策略，有著密不可分的聯系。

對于分解之后的基本問題，我們就可以使用一些基本的策略求解，因為容易，比如枚舉。

核心策略

1. 分：大問題–> 小問題 --> 基本問題
2. 治：解決基本問題
3. 合：將基本問題的解合并，得到原問題的解
   
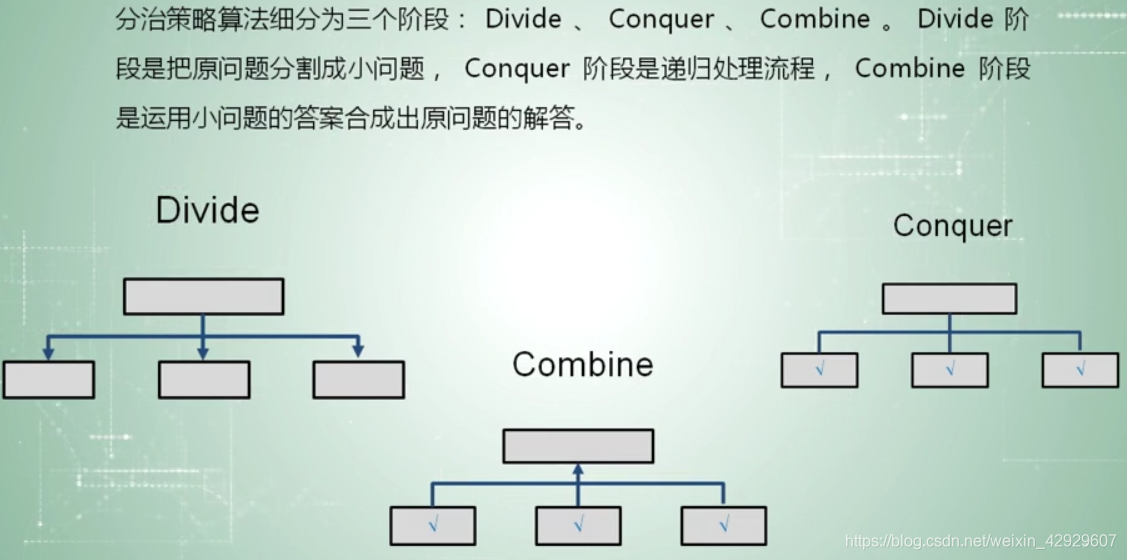
   抽象的理論內容，很重要，我們把握其核心思想和本質，但是，想要理解抽象，我們更應該解決實際問題，在實際問題中理解抽象概念，達到融會貫通。

基本框架程序

1. 理解問題
2. 分解問題，找到自己認識的部分；或者，從最簡單情況出發，遞推地分析一下
3. 獲得簡單問題的求解辦法
4. 將大問題遞歸地分解為簡單問題去處理
5. 將每個小問題的解合并

如此抽象，說了也白說，直接上例子。

歸并排序

最難點：【合】的策略，合無定法！

分治策略與遞歸的對應關系

分：進行遞歸操作
治：遞歸終止條件和處理辦法
合：遞歸處理辦法

對于歸并排序

1. 分：將數組不斷進行二分，直到其剩余1個元素
2. 治：對于1個元素，一定是有序的，就可以將其作為基本問題的解返回
3. 合：對于基本問題的解，需要讓其合并后有序，因此合并需要專門的一些策略，針對歸并排序特點進行設計。

合是最難的，因為合無定法，每種問題的每種解法，可能都不一樣。

看代碼：

#include <ctime>
#include <iostream>
using namespace std;// 給你一個規模很小的數組，并且告訴你分兩半，每一半都是有序的，讓你給合起來依然有序
// 合
void merge(int data[], int buffer[], int min, int mid, int max) {int first_mid_pointer = min;		// data[min, mid]int second_mid_pointer = mid + 1;	// data[mid+1, max]int buffer_pointer = min;			// buffer[min, max]while (first_mid_pointer <= mid && second_mid_pointer <= max) {if (data[first_mid_pointer] <= data[second_mid_pointer]) {buffer[buffer_pointer] = data[first_mid_pointer];buffer_pointer++;first_mid_pointer++;}else{buffer[buffer_pointer++] = data[second_mid_pointer++];}}// 傳遞剩余部分if (first_mid_pointer <= mid) {while (first_mid_pointer <= mid && buffer_pointer <= max) {buffer[buffer_pointer++] = data[first_mid_pointer++];}} else {while (second_mid_pointer <= max && buffer_pointer <= max) {buffer[buffer_pointer++] = data[second_mid_pointer++];}}}// 歸并排序
void merge_sort(int data[], int buffer[], int min, int max) {// 治if (min >= max)return;if (min < max){// 分int mid = (max + min) / 2;	// + ;not -merge_sort(data, buffer, min, mid);merge_sort(data, buffer, mid + 1, max);// 合（“治”之后才會執行）merge(data, buffer, min, mid, max);// buffer result --> datafor (int i = min; i <= max; i++) {	// 注意起點和終點，注意“=”data[i] = buffer[i];}}
}int main()
{clock_t start, end;for (int n = 64; ; n *= 2) {// initializationint *a = new int[n];for (int i = 0; i < n; i++) {a[i] = rand() % 10000 + 1;}// merge sortstart = clock();int length = n; //sizeof(a) / sizeof(a[0]);int *buffer = new int[length];merge_sort(a, buffer, 0, length - 1);end = clock();cout << "N = " << n << "   time = " << end - start << endl;if ((end - start)*2 > 180000)	// predict: more than 3 minutes,stop!break;}return 0;}

類似版本的代碼

#include <iostream>
using namespace std;// combine function
// data sequence: min to max
void combine(int data[], int buffer[], int min, int mid, int max) {// NOTE: max = length of array - 1int before_mid_pointer = min;		// data[min,mid]int after_mid_pointer = mid + 1;	// data[mid+1,max]int buffer_pointer = min;			// buffer[min,max]while (before_mid_pointer <= mid && after_mid_pointer <= max){if (data[before_mid_pointer] <= data[after_mid_pointer])buffer[buffer_pointer++] = data[before_mid_pointer++];elsebuffer[buffer_pointer++] = data[after_mid_pointer++];}// process the rest of data that is not be compared// add them to buffer directlywhile (before_mid_pointer <= mid && buffer_pointer <= max){buffer[buffer_pointer++] = data[before_mid_pointer++];}while (after_mid_pointer <= max && buffer_pointer <= max){buffer[buffer_pointer++] = data[after_mid_pointer++];}// add buffer to datafor (int i = min; i <= max; i++) {data[i] = buffer[i];}}// 自始至終，我們都是使用一個data和一個buffer，通過指針值“虛擬地”分割和排序。
// merge sort
void merge_sort(int data[], int buffer[], int min, int max) {if (max > min) {// divideint mid = (max + min) / 2;merge_sort(data, buffer, min, mid);merge_sort(data, buffer, mid + 1, max);// combine: sort two sorted arrays using specified methodcombine(data, buffer, min, mid, max);} else {// conquer: only 1 elementreturn;}
}int main() {int data[8] = { 1,3,5,0,100,4,33,7 };int buffer[8] = { 0 };merge_sort(data, buffer, 0, 7);for (int i = 0; i < 8; i++) {cout << buffer[i] << "  ";}return 0;
}

小結

分治思想，用一個成語就是庖丁解牛，完整的牛我們搞不懂，就將其合理地拆解，分成小部分，然后就可以搞定了。

還需要大量實例去體會分、治、合的思想策略。

我們知道了分治策略與遞歸思想的結合。

治理的是基本問題，也就是遞歸的結束條件和結束時候的處理辦法。

而分則是遞歸調用過程，它指明了我們應該如何調用遞歸函數去分割問題，使其更簡化。

最后，合，則是在某個遞歸函數返回之后的處理辦法，它也在遞歸處理過程內，只有遞歸返回后，才會執行，用于合并返回的基本問題的解，從而得到最終的復雜問題的解。

對于歸并排序，我們有一個比較神奇的點，那就是，自始至終，data和buffer都使用的是一個，而所謂的分割，都是通過虛擬的指針來實現的，我們并沒有真地將其分割！

算法學習策略

1. 原理與思想本質
2. 實例與圖解
3. 實際問題分析
   1. 抽象
   2. 實現

需要這幾個過程，才能真正體會算法思想的精髓，通過大量實例和圖解，能夠更好地理解算法，理解思想本質。