1 圖的基本概念

無向圖：

簡而言之，邊不帶方向的圖就是無向圖。
有向圖：

簡而言之，邊帶方向的圖就是有向圖。
特殊定義：

有限圖：邊數和頂點數都是有限個的圖。
n階圖：n個頂點的圖。
零圖：沒有邊的圖。
平凡圖：只有一個頂點，而且沒有邊的圖（1階零圖）。
空圖：沒有頂點的圖（自然也沒有邊，空圖也是零圖）。

環：邊的兩頭都是同一個頂點，這個邊就是環。
孤立點：沒有邊連著的點。
無向圖頂點的度：
頂點的度：一個頂點有幾個邊連接著，就是幾度(注意，環會提供兩度）。
懸掛頂點：度數為1的頂點。
懸掛邊：懸掛頂點連著的那個邊。
最小度：一個圖中各頂點度數中最小的數值。
最大度：一個圖中各頂點度數中最大的數值。
有向圖頂點的度

出度：從一個頂點出去的邊的邊數。
入度：從外面進一個頂點的邊數。
總度數：總度數=入度+出度。
最大入度：圖中所有頂點中入度最大的數值。
最大出度：圖中所有頂點中出度最大的數值。
最小入度：圖中所有頂點中入度最小的數值。
最小出度：圖中所有頂點中出度最小的數值。
握手定理

圖的頂點度數和數量是邊數的2倍，證明很顯然，一個邊會提供兩度。

由握手定理推出的推論，圖的奇度頂點為偶數個。證：如果有奇數個奇度頂點，那么圖的總度數必定為奇數，而根據握手定理，總度數必定為偶數，矛盾。
度數列

度數列就是將一個圖中所有頂點的度按一定順序寫出來。注意：判斷一個數列是否能構成度數列，先看是否滿足握手定理推論(偶數個奇度頂點）。
簡單圖

簡單圖：不存在平行邊的圖，即每兩個頂點之間最多只有一條邊。
完全圖和正則圖

無向完全圖就是任一個頂點都與其他所有頂點之間有邊，邊數：n(n-1)/2，最大度=最小度=n-1，記作Kn。
k—正則圖：每個頂點都是k度的無向簡單圖。
圈圖和輪圖

圈圖Cn就是圍成一個圈的圖，輪圖Wn就是在圈圖Cn-1中放一個點，再把這個點和其它所有點連起來。（注：圈圖頂點數>=3，輪圖頂點數>=4）
子圖

子圖：從母圖中選一些點和邊構成的圖就是該母圖的子圖。
生成子圖：刪邊不刪點。
導出子圖：選母圖中一些點構成點集，這些點和以它們為端點的邊構成的圖就是這個這個點集的導出子圖；選母圖中一些邊構成邊集，這些邊和與它們關聯的頂點構成的圖就是這個這個邊集的導出子圖；
補圖

補圖：將原圖補成完全圖，再將原圖中有的邊刪掉，就是補圖。
圖的同構

同構：同構就是指同一個圖的不同畫法。找非同構的方法就是根據條件找到不同的度數列，然后試著畫出不同結構的圖（類似有機化學中找同分異構體）。

2 圖的連通性

通路和回路

簡單回路：回路中所有邊各異。初級回路（圈）：回路中所有點各異（自然，邊也各異，所以初級回路是簡單回路）。

無向圖的連通性和連通分支

連通就是兩點之間有通路（能從一點走到另一點）；連通圖就是任意兩點都連通的圖（特別的，平凡圖是連通圖）；連通分支就是圖中的一個不跟其它部分連通的部分，連通圖只有一個連通分支。
短程線和距離

短程線就是兩點之間最短的通路，其長度稱作距離。
點割集和邊割集

點割集：刪掉圖中的一些點后，圖的連通分支數增加，且這些點缺一不可，這些點的集合就是點割集，如果點割集只有一個點，這個點叫做割點；邊割集：刪掉圖中的一些邊后，圖的連通分支數增加，且這些邊缺一不可，這些邊的集合就是邊割集，如果邊割集只有一個點，這個點叫做割邊或橋。
點連通度和邊連通度

點割集的元素數就是點連通度，如果沒有點割集就是（總頂點數-1）；邊割集的元素數就是邊連通度。
有向圖的弱連通與強連通

弱連通就是有向圖忽略方向以后為連通圖，強連通就是有向圖中任意兩個頂點相互可達。

3 圖的矩陣表示

無向圖的關聯矩陣

無向圖關聯矩陣：行代表邊，列代表頂點。數值為0代表不關聯，1代表關聯，2代表成環。特殊性質：每一列的和為2，因為每一列代表一個邊所關聯的頂點，一個邊關聯兩個頂點；每一行的和該頂點的度，顯而易見；所有數加起來是邊數的二倍,因為根據握手定理，總度數之和為邊數的二倍。
有向無環圖的關聯矩陣


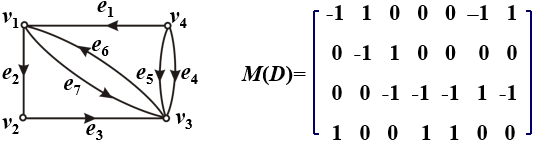
有向無環圖關聯矩陣：行代表邊，列代表頂點。數值為1代表邊從頂點出去，0代表不關聯，-1代表邊從頂點進來。
鄰接矩陣



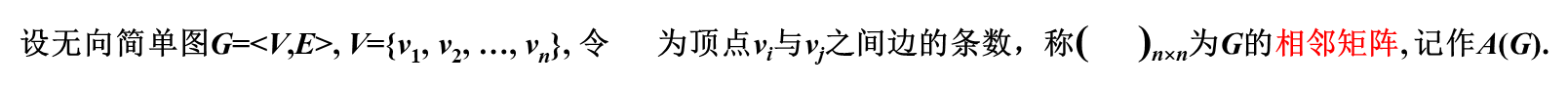
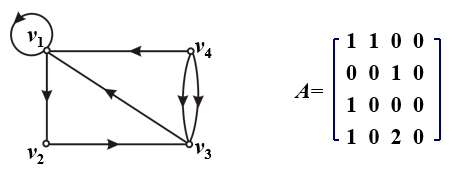
行和列都是頂點，矩陣數值是列對應頂點鄰接到行對應頂點的邊的條數。
利用鄰接矩陣求各個長度的通路和回路數量

說明:A^n中的元素表示一個頂點到另一個頂點之間距離為n的通路數。所以可以通過矩陣乘法求鄰接矩陣的n次方求有向圖中的通路和回路數。例：

可達矩陣

可達矩陣；矩陣的行和列都是頂點，只要一個頂點可達另一個頂點，就為1，否則是0，無向圖連通當且僅當這個圖的可達矩陣的元素全為1，有向圖強連通當且僅當這個圖的可達矩陣的元素全為1。
鄰接矩陣轉可達矩陣的方法
假設圖的頂點數為n，由鄰接矩陣(A)計算可達矩陣§的方法如下：
1.B = A + A ^ 2 + … + A ^ (n-1);
2.將B的對角線元素全變成1，將B的非零元素全變為1.

4 幾種特殊的圖

4.1 二部圖

二部圖定義

二部圖：如果能將一個圖的所有頂點分為兩份，圖中的所有邊的兩個端點一個再一份里，一個在另一份里，這樣的圖就叫做二部圖。完全二部圖就是圖中每一個頂點都跟另一份中的所有頂點相鄰的二部圖。
二部圖的判別定理（充要條件）

證明如下：

染色法判斷二部圖
染色法：從圖的一個頂點開始，將它染成紅色，所有與它鄰接的頂點染成白色，所有與剛剛染成紅色的頂點相鄰的頂點染成紅色，如此反復，如果能不沖突地將圖中所有點都染上色，說明這個圖是二部圖，舉例如下：

匹配

匹配：在二部圖中選一部分互不相鄰的邊，這些邊就是原二部圖的一個匹配。
極大匹配：如果在已經選好的匹配中，再加任意一條邊都不再是匹配，那么這個匹配就是極大匹配。
最大匹配：一個圖中邊數最多的匹配(最大匹配是極大匹配)。
完備匹配：如果V1<V2，圖中一個匹配的邊數與V1相等，這個匹配叫做完備匹配。
完美匹配：V1=V2，匹配中的邊數與V1,V2相等。
存在完備匹配的條件

Hall定理：有完備匹配當且僅當任取V1中K個頂點，這K個頂點至少和V2中的K個頂點相鄰。(充分必要條件）

t條件：二部圖中能找到這樣的正整數t，使得V1中每個頂點至少關聯t條邊，V2中每個頂點至多關聯t條邊，則有完備匹配。（充分非必要條件）
二部圖的應用 (完備性問題)
可以將匹配、完備問題建模成二部圖問題，然后使用Hall定理或者t條件來解決，例：

本題是一個完備性問題，化成二部圖以后找完備匹配即可。

（1）可用t條件找到t=2，（2）找不到t，但是滿足相異性條件，(3)找不到t，且不滿足相異性條件。

4.2 歐拉圖

歐拉圖定義

圖中能找到一個經過所有邊僅一次，且經過所有頂點的回路，這個圖就是歐拉圖。（歐拉回路是簡單回路，但不一定是初級回路，也就是說同一頂點可以多次經過)。
無向圖的歐拉圖判定定理

無向圖是連通的，而且沒有奇度頂點，就有歐拉回路，就是歐拉圖。圖是連通的，且僅有兩個奇度頂點，就有歐拉通路，但沒有歐拉回路。
有向圖的歐拉圖判定定理

有向圖是連通的，而且所有頂點入度等于出度，就有歐拉回路，是歐拉圖。是連通且一個頂點入度比出度大1，一個頂點出度比入度大1，其余入度等于出度，就有歐拉通路。
歐拉圖的應用（一筆畫問題）

戈尼斯堡七橋不能不重復的走完，因為有BCD三個奇度頂點，所以無歐拉通路。

4.3 哈密頓圖

哈密頓圖定義

圖中能找到過所有頂點且僅過一次的回路，那么這個圖就是哈密頓圖（對邊無要求）
顯然哈密頓通路是初級通路，哈密頓回路是初級回路，特別的，定義平凡圖是哈密頓圖。
哈密頓圖的必要條件

如果一個圖是哈密頓圖，那么刪去這個圖中n個頂點后，所得圖的連通分支數一定p<=n。該定理是哈密頓圖的必要條件，一般用來證明一個圖不是哈密頓圖，即找到一個有n個頂點的點集，刪去以后剩下的圖的連通分量數大于n，那么這個圖一定不是哈密頓圖，如下圖中:

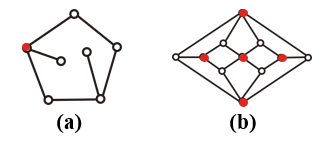
（a）刪去紅色點后有兩個連通分量，不是哈密頓圖，實際上有割點的圖不是哈密頓圖，（b）刪去5個紅點以后有6個連通分量，不是哈密頓圖。一般來說使用該定理時優先刪去度數大的頂點。
哈密頓回路（通路）的充分條件

簡單無向圖中，任兩個不相鄰的頂點度數和>=n-1則有哈密頓通路，>=n則有哈密頓回路。如果簡單無向圖的最小度>=n/2，則是哈密頓圖，如果一個有向圖略去方向以后所得無向圖中含有子圖Kn（n階完全圖），則有哈密頓通路。
哈密頓圖的應用（周游問題）

先將本題轉化成圖論問題，將每個人看作點，如果兩個人能交談，就連上邊，畫出圖以后，如果能找到哈密頓回路，那么就能坐成一圈。

4.4 平面圖

平面圖的定義

平面圖的概念比較抽象：如果一個圖可以邊不相交地畫在平面上，那么就是平面圖。如果無論怎么話都無法使邊不相交，就不是平面圖，如下圖：

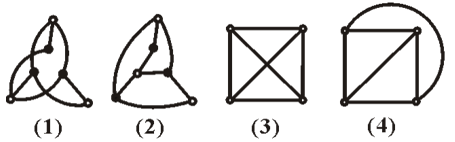
(1)雖然有邊相交，但是一個圖并沒有規定畫成什么樣子，只要頂點個數，邊的個數，頂點和邊之間的關聯不變，那么兩個圖就是同構的，（1）的一種同構為（2），邊不相交，所以圖（1）是平面圖，（2）是（1）的平面嵌入。（3）（4)同理。
平面圖的面和次數

對于面的邊界的判斷容易出錯，如下：

注意到外部面R0的邊界中，d應該記作兩次，因為面的邊界是以回路定義的；兩個不同的回路之間要用逗號隔開。
平面圖面的次數和與邊數的關系

極大平面圖

簡單平面圖中，任意再加一條邊就不是平面圖了，這個平面圖就是極大平面圖。
極大平面圖的充分必要條件

一個圖是極大平面圖的充要條件是它的所有面的次數都是3，注意外部面的次數也應該是3.
平面圖歐拉公式

一個連通的平面圖里，頂點數-邊數+面數=2。

更一般地：在有多個連通分支時，頂點數-邊數+面數=連通分支數+1。

注意：此處的l是面次最小值。利用該定理可以證明不是平面圖，例如：

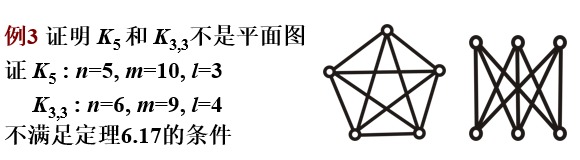
平面圖的充要條件（庫拉圖斯基定理）

首先說明什么是同胚和收縮：

同胚就是兩個圖同構，或者經過反復插入消去二度頂點后同構。
收縮就是將兩個點之間的邊刪掉，然后將這兩個點“捏”到一起，變成一個點。
庫拉圖斯基定理就是：圖是平面圖當且僅當這個圖不與K5,K3,3同胚，也無可收縮為K5，K3,3的子圖。庫拉圖斯基定理比較難理解，通過如下 實例可便于理解：

一般來說，如果一個圖含與K5,K3,3同胚的子圖，那么也含能收縮到K5，K3,3的子圖。因為收縮比同胚要直觀，所以這里用收縮來解釋這兩道例題：
第一個圖可以先刪除圖中所有黑色的邊，之所以可以刪除，是因為我們要找的是可以收縮為K5或K33的子圖，然后最上和最下兩個頂點可以收縮到左邊相鄰的頂點（也可以理解成刪除這個點），最后就得到了K3,3，所以不是平面圖；第二個圖同理，刪除兩條黑邊，然后收縮最下面的兩個點到相鄰的點（也可以理解成刪除這個點），最后收縮成了K5，所以不是平面圖。
對偶圖

簡而言之，對偶圖就是，原圖的點變成面，面變成點。為了實現這個變換，將原圖中的每個面（包括外部面）中畫一個點，如果兩個面原來相鄰，那就通過每一條相鄰邊都畫一條新的線來連接新的兩個點，最后畫出來的圖就是對偶圖，如下圖所示：

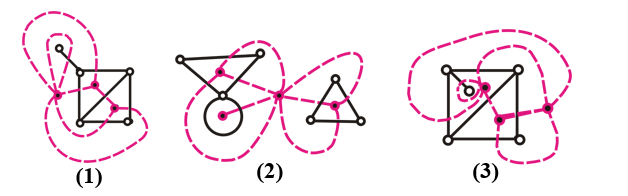
實線和空心點是原圖，紅色虛線和實心點是對偶圖。
對偶圖的性質


橋變環，環變橋，邊數不變，頂點數和面數互換，面的次數對應點的度數。

5 無向樹

無向樹的定義

如果一個圖是連通的而且沒有回路，這個圖就是樹。
無向樹的性質

以下三條任意滿足兩條，圖就是樹：
1.連通
2.無回路
3.m=n-1

6 生成樹

生成樹的定義
一個無向連通圖的生成子圖（刪邊不刪點）如果是樹，這個樹就是這個點的生成樹。
生成樹的存在性

無向連通圖都有生成樹，可用破圈法證明。
最小生成樹

總權值最小的生成樹就是最小生成樹。找最小生成樹的方法如下：
克魯斯卡爾算法

簡而言之，從權最小的邊開始按從小到大開始選擇，如果不與已經選好的邊構成回路，就選擇這條邊，直到對所有邊的選擇結束，就找到了最小生成樹。例：

紅色為選擇的，黑色是不選擇的，注意，環不選擇，如果有權值一樣的邊，則隨便選擇一個，然后選擇另一個。