單純形法是一種解線性規劃問題的算法，其求解過程是通過構造一個單純形表實現的，具體步驟如下：

單純形法步驟：

1.將線性規劃問題化為標準形式

標準形式如下：

其特點是：
(1) 目標函數求最大值（有時求最小值）
(2) 約束條件都為等式方程，且右端常數項 bi 都大于或等
于零
(3) 決策變量 xj 為非負

為了方便使用單純形法來求解線性規劃問題，我們需要將現有問題化為標準形式，其方法如下：

(1) 目標函數的轉換

(2) 無約束變量的轉換

(3) 約束方程由不等式轉為等式

(4) 小于等于0的變量的轉換

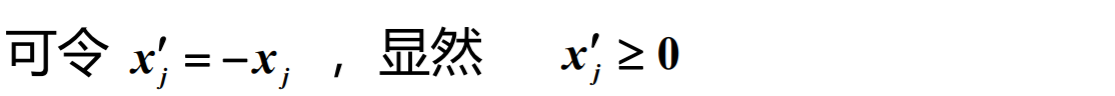
以下為一將問題轉化為標準形式的例子：

2.列出單純形表

對于已經化為標準型的線性規劃問題

其對應的單純形表如下：

其中：

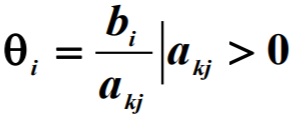
例如以下已經化為標準型的線性規劃問題：

其單純形表如下：

3.進行最優性檢驗

如果表中所有的檢驗數都小于等于0，則表中的基可行解就是問題的最優解，計算停止，否則進行下一步。

4.從一個基可行解轉換到另一個目標值更大的基可行解，列出新的單純形表

5.重復3、4直到計算結束為止

重復3、4步驟，直到表中所有的檢驗數都小于等于0，計算結束，表中的基可行解就是問題的最優解。

舉例

將問題化為標準型，加入松弛變量x3，x4：

運用單純形表求解：

注：本次求解進行了兩次迭代，上圖把初始單純形表和兩次迭代時的單純性表從上到下拼接在了一起。

單純形法matlab實現

Simplex_eye.m：

function [x_opt, fx_opt, iter, Table] = Simplex_eye(A,b,c)% A = [2 -3 2 1 0; 1/3 1 5 0 1];
% b = [12 20]';
% c = [1 2 1 0 0]'; %初始單純型表
Table = zeros(size(A,1)+1, size(A,2)+1);
Table(1:size(A,1), 1:size(A,2)) = A;
Table(size(A,1)+1, 1:size(A,2)) = c';
Table(1:size(A,1), size(A,2)+1) = b;[m, n] = size(Table);  %m為行數，n為列數base = Find_indentity(A);     %調用函數，找單位矩陣的列下標iter = 0;  %迭代次數while sum(Table(size(Table,1), 1:size(Table,2))>0)
%循環條件:當存在大于零的檢驗數就繼續循環iter = iter + 1;index_col = find(Table(m,:) == max(Table(m,:))); %找最大檢驗數所在列pos = find(Table(1:m-1, index_col) > 0);temp = zeros(1,size(pos,2));for i = 1:size(pos,1)temp(i) = Table(pos(i), n)/Table(pos(i), index_col);endindex_row = pos(temp == min(temp));          %找主元行%以下做初等行變換Table(index_row,:) = Table(index_row, :)./Table(index_row,index_col);for i = 1:index_row-1Table(i,:) = Table(i,:)-Table(i,index_col)*Table(index_row,:);endfor i = index_row+1 : mTable(i,:) = Table(i,:)-Table(i,index_col)*Table(index_row,:);endbase(index_row) = index_col;    %換基，把第index_row個基換成index_col
endx_opt = zeros(1,size(c,2));
for i = 1:size(base, 1)x_opt(1,base(i)) = Table(i,n);
endfx_opt = -1*Table(size(Table,1), size(Table,2));end

找單位矩陣列下標 Find_indentity.m：

function [index] = Find_indentity(A)function [index] = Find_indentity(A)
[m,n] = size(A);
index = zeros(m,1);for i = 1:mtemp = find(A(i,:)==1);if size(temp,2) == 1index(i,1) = temp;elsefor t = 1:size(temp,2)flag = 0;for r = 1:i-1if A(r, temp(1, t)) ~= 0flag = 1;break;endendfor r = i+1:mif A(r, temp(1, t)) ~= 0flag = 1;break;endendif flag == 0index(i,1) = temp(1, t);break;endendend
endend