物理層解決如何在連接各種計算機的傳輸媒體上傳輸數據比特流,而不是指具體的傳輸媒體。
確定與傳輸媒體接口有關的特性
- 機械特性:定義物理連接的特性,如規格、接口形狀、引線數目、引腳數目、排列
- 電氣特性:規定傳輸二進制位時的電壓范圍、阻抗匹配、傳輸速率、距離限制等
- 功能特性:指明某種電平代表的意義,是0還是1
- 規程特性:定義各物理線路工作的規程和時序關系
數據通信基礎

數據:傳送信息的實體,通常是有意義的符號序列
信號:數據的電氣/電磁表現,是數據在傳輸過程中的存在形式
- 數字信號
- 模擬信號
信源:產生和發送數據的源頭
信宿:接收數據的重點
信道:信號的傳輸媒介,有方向,一條通信線路往往包含一條發送信道和接受信道。
三種通信方式:
- 單工通信:一條信道
- 半雙工通信:兩條信道
- 全雙工通信:兩條信道
數據傳輸方式:
- 串行傳輸:速度慢、費用低、適合遠距離
- 并行傳輸:速度快,費用高、適合近距離(計算機內部)
碼元:是指用一個固定時長的信號波形(數字脈沖),代表不同離散數值的基本波形。是數字通信中數字信號的計量單位。離散狀態的個數M,則稱該信號為M進制碼元。時長稱為碼元寬度。
M進制碼元可以攜帶logM個比特的信息量
速率也叫數據率,是指數據的傳輸速率,表示單位時間內傳輸的數據量,可以用碼元傳輸速率和信息傳輸速率表示。
碼元傳輸速率:別名碼元速率,波形速率,調制速率,符號速率。單位是波特(Baud=碼元/秒)
碼元速率和進制數無關
信息傳輸速率:別名信息速率,比特率,表示單位時間內數字通信系統傳輸的二進制碼元( 即比特數),單位是比特/秒
信息傳輸速率=碼元傳輸速率*logM
帶寬:最高數據率,單位是b/s
系統傳輸速率比較的是信息傳輸速率
香農定理和奈氏準則
影響失真程度的因素:碼元傳輸速率、信號傳輸距離、噪聲干擾、傳輸媒體質量
碼間串擾
信道帶寬:信道能通過的最高頻率和最低頻率之差
需要注意的是只有在這兩個地方帶寬指的是通信中的帶寬:最高頻率和最低頻率之差
碼間串擾:接收端收到的信號波形失去了碼元之間清晰界限的現象
奈奎斯特定理
奈氏準則:在理想低通(無噪聲、帶寬受限)條件下,為了避免碼間串擾,極限碼元傳輸速率為2W Baud,W是信道寬度,單位是Hz.
理想低通信道下的極限數據傳輸率=2WlogV b/s V表示碼元的進制
- 碼元傳輸速率如果超過2W,則會出現嚴重的碼間串擾
- 頻帶越寬(即能通過的信號高頻分量越多),就可以用更高的速率進行碼元的有效傳輸
- 奈氏準則給出的是碼元傳輸速率的限制,并沒有對信息傳輸速率給出限制
- 由于碼元的傳輸速率受奈氏準則的制約,所以要提高數據的傳輸速率就必須設法使得每個碼元能夠攜帶更多的信息量。這就需要采用多元制的調制方法
香農定理
信噪比=信號的平均功率/噪聲的平均功率,S/N,用分貝db作為度量單位
即:信噪比(db)=10lg(S/N)
香農定理:在帶寬受限而且有噪聲的信道中,為了不產生誤差,信息的數據傳輸速率有上限值。
信道的極限傳輸速率=Wlog(1+S/N) b/s
注意這里的S/N是沒有單位的,只是一個比值,如果題目中的信噪比以db為單位,則需要進行轉換。
- 信道的帶寬或信道中的信噪比越大,則信息的極限傳輸速率越高
- 對一定的傳輸帶寬和一定的信噪比,信息傳輸速率的上限就確定了
- 只要信息的傳輸速率低于信道的極限傳輸速率,就一定能夠找到某種方法來實現無差錯傳輸
- 香農定理給出的為極限傳輸速率,實際上達不到
- 若信道帶寬W和信噪比S/N沒有上限,那么信道的極限信息傳輸速率也就沒有上限
兩個定理的比較
奈氏準則解決的是帶寬受限無噪聲條件下碼間串擾問題,規定碼元傳輸速率為2W Baud
香農定理解決的是帶寬受限有噪聲條件下最高的信息傳輸速率,規定不超過Wlog2(1+S/N) b/s
極限數據傳輸速率=min(2Wlogv,Wlog(1+S/N))
編碼調制
基帶信號:信源發送的信號,基帶信號的傳輸叫做基帶傳輸(數字信號)
寬帶信號:對基帶信號進行調制后,寬帶信號的傳輸叫做寬帶傳輸(模擬信號)
在傳輸距離比較近的時候采用基帶傳輸(近距離衰減小,信號內容不易發生變化)
在傳輸距離比較遠的時候采用寬帶傳輸(遠距離衰減大,即使信號變化大也能最后過濾出基帶信號)

數字數據編碼為數字信號
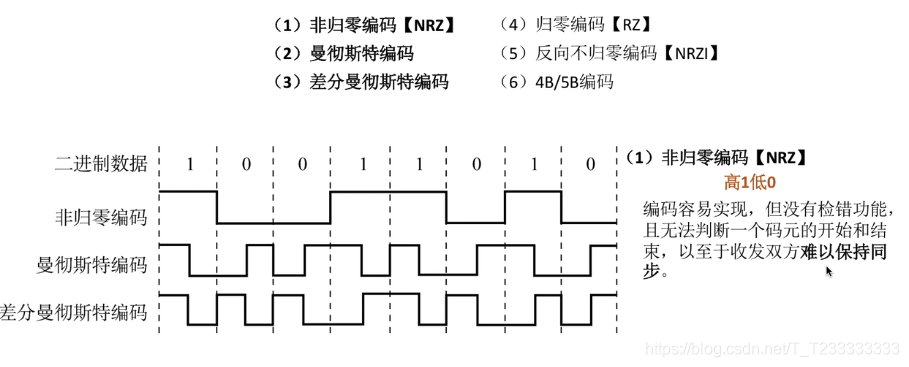

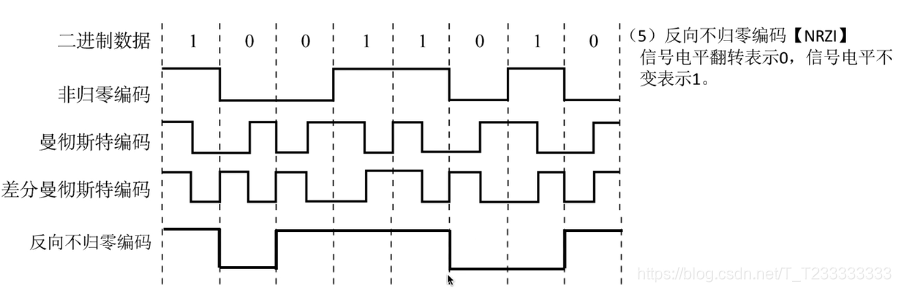
曼徹斯特編碼:實現自同步

即兩個碼元表示一個比特


數字數據編碼為模擬信號
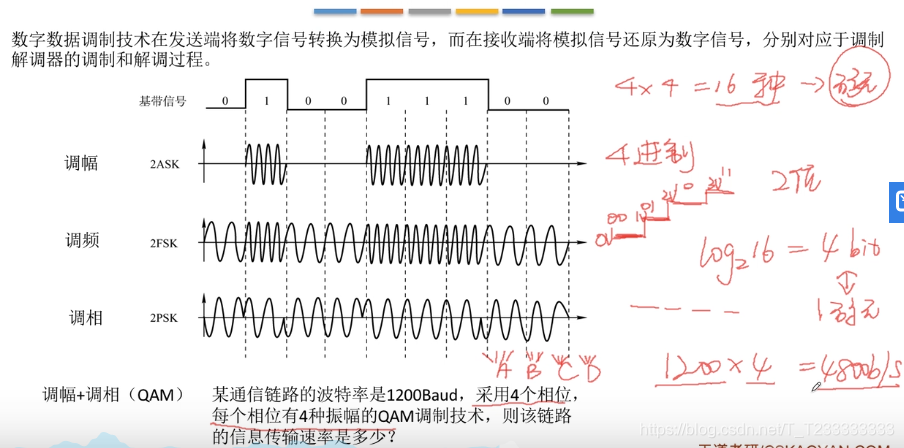
模擬數據編碼為數字信號

模擬數據編碼為模擬信號

傳輸介質及其分類
傳輸介質也稱作傳輸媒體,是數據傳輸的物理通路。
傳輸媒體并不是物理層

傳輸介質:
- 導向性傳輸介質:銅線/光纖
- 非導向性傳輸介質:自由空間
雙絞線

- 便宜
- 遠距離傳輸需要放大器/中繼器對信號增強
同軸電纜

- 抗干擾能力強
- 傳輸距離遠
光纖
傳輸的是光脈沖,而不是電脈沖。


- 傳輸損耗小,中繼距離長,對遠距離傳輸經濟
- 抗雷電和電磁干擾性能好
- 無串音干擾,保密性好
- 體積小,重量輕
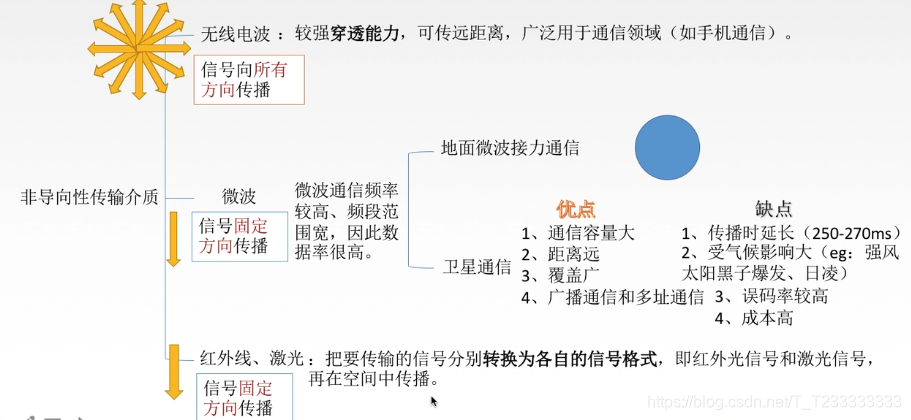
非導向性傳輸介質
- 無線電波
- 微波
- 紅外線、激光
物理層設備
中繼器


集線器(多口中繼器)
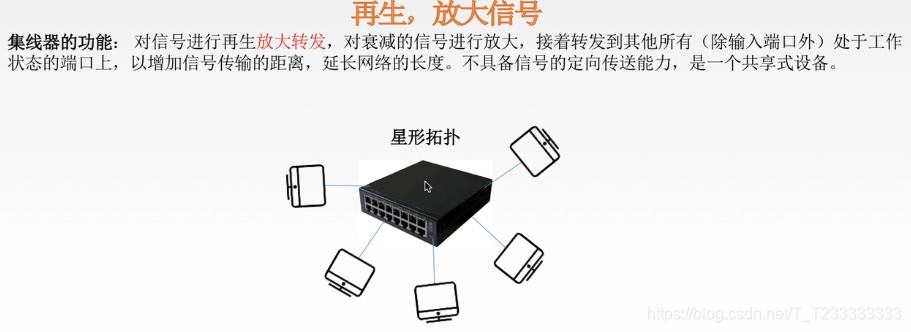
集線器不能分割沖突域——>連在集線器上的工作主機平分帶寬



















