代換法

1. 猜測復雜度
2. 驗證是否滿足遞歸式（使用歸納法）
3. 找到常數應該滿足的條件
4. 針對基本情況，常數足夠大時總是成立的

需要注意的是，我們猜測的復雜度有可能不滿足遞歸式，這個時候就要通過減去一些低階項來使得歸納成立。

對遞歸式$T(n)=4T(n/2)+Cn$
我們假設$T(n)=\Theta (n^2)?C_1{n}^2?C_{2}n$，下面進行歸納證明：
假設k<n時$T(k)?C_1{k}^2?C_{2}k$
$T(n)?4(C_1\frac{n^2}{4}?C_2\frac{n}{2})+Cn=C_1{n}^2?C2n?(C2?C)n?C_1{n}^2?C_{2}n$當$C_2>C$時成立。

對于基本情況，當$C_1$足夠大的時候成立。

因此，$T(n)=\Theta (n^2)$

遞歸樹法

• 將遞歸式寫成遞歸式求和的形式
• 逐層求和：一般來講會有規律

對于$T(n)=T(n/4)+T(n/2)+n^2$

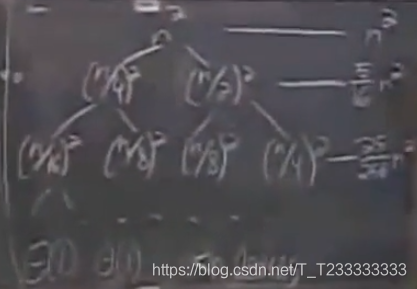
發現系數是等比數列，進行求和

主方法

只能應用到特定的遞歸式上：$T(n)=aT(n/b)+f(n),a>1,b>1,f(n)$ is asymptotically postive

比較$f(n)$和$n^{lo{g}_{b}a}$

• 如果$f(n)$多項式地小于$n^{lo{g}_{b}a}$，$T(n)=\Theta (n^{lo{g}_{b}a})$
• 如果$f(n)=\Theta (n^{lo{g}_{b}a}?{lo{g}_2^n}^k)，k?0$，$T(n)=\Theta (n^{lo{g}_b^a}?{lo{g}_2^n}^{k+1})$
• 如果$f(n)$多項式地大于$n^{lo{g}_{b}a}$，而且$af(n/b)?(1??)f(n)$，則$T(n)=\Theta (f(n)$

其他

雖然上面的方法可以解決絕大部分問題，但是還有一些問題無法用上面的方法進行解決，需要使用一定的數學技巧。

例如，如果遞歸式中出現了指數運算，我們首先應該用冪次代替n，然后變成除法運算再得到結果。

例如：$T(n)=T(\sqrt[3]{n})+1$

我們首先令$n=2^k$，即$k=lo{g}_{2}n$。則：
$T(n)=T(2^{k/3})+1=...=T(1)+lo{g}_{3}k=lo{g}_{3}lo{g}_{2}n=loglogn$