分類預測 | MATLAB實現GWO-BiGRU-Attention多輸入分類預測

預測效果

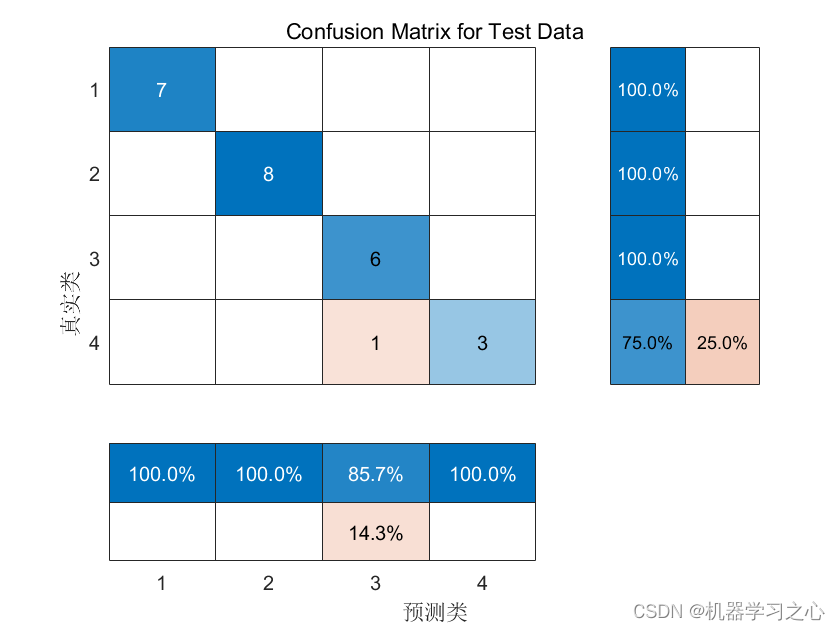
基本介紹

1.GWO-BiGRU-Attention 數據分類預測程序
2.代碼說明：基于灰狼優化算法（GWO）、雙向門控循環單元網絡（BiGRU）和注意力機制的數據分類預測程序。
程序平臺：要求于Matlab 2023版及以上版本。
特點：
1、多行變量特征輸入。
2、GWO優化了學習率、神經元個數等參數，方便增加維度和優化其他參數。
3、適用于軸承故障、變壓器油氣故障、電力系統輸電線路故障區域、絕緣子、配網等領域的識別、診斷和分類。
可直接替換數據，使用EXCEL表格導入，無需大幅修改程序。代碼內部有詳細注釋，便于理解程序運行。

程序設計

• 完整程序和數據獲取方式1：同等價值程序兌換；
• 完整程序和數據獲取方式2：私信博主回復 MATLAB實現GWO-BiGRU-Attention多輸入分類預測獲取。

%%  劃分訓練集和測試集
P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);%%  數據歸一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);
%%  個體極值和群體極值
[fitnesszbest, bestindex] = min(fitness);
zbest = pop(bestindex, :);     % 全局最佳
gbest = pop;                   % 個體最佳
fitnessgbest = fitness;        % 個體最佳適應度值
BestFit = fitnesszbest;        % 全局最佳適應度值%%  迭代尋優
for i = 1 : maxgenfor j = 1 : sizepop% 速度更新V(j, :) = V(j, :) + c1 * rand * (gbest(j, :) - pop(j, :)) + c2 * rand * (zbest - pop(j, :));V(j, (V(j, :) > Vmax)) = Vmax;V(j, (V(j, :) < Vmin)) = Vmin;% 種群更新pop(j, :) = pop(j, :) + 0.2 * V(j, :);pop(j, (pop(j, :) > popmax)) = popmax;pop(j, (pop(j, :) < popmin)) = popmin;% 自適應變異pos = unidrnd(numsum);if rand > 0.95pop(j, pos) = rands(1, 1);end% 適應度值fitness(j) = fun(pop(j, :), hiddennum, net, p_train, t_train);endfor j = 1 : sizepop% 個體最優更新if fitness(j) < fitnessgbest(j)gbest(j, :) = pop(j, :);fitnessgbest(j) = fitness(j);end% 群體最優更新 if fitness(j) < fitnesszbestzbest = pop(j, :);fitnesszbest = fitness(j);endendBestFit = [BestFit, fitnesszbest];    
end
————————————————
版權聲明：本文為CSDN博主「機器學習之心」的原創文章，遵循CC 4.0 BY-SA版權協議，轉載請附上原文出處鏈接及本聲明。
原文鏈接：https://blog.csdn.net/kjm13182345320/article/details/130462492

參考資料

[1] https://blog.csdn.net/kjm13182345320/article/details/129679476?spm=1001.2014.3001.5501
[2] https://blog.csdn.net/kjm13182345320/article/details/129659229?spm=1001.2014.3001.5501
[3] https://blog.csdn.net/kjm13182345320/article/details/129653829?spm=1001.2014.3001.5501