目錄:
- 介紹:
- 代碼:
- 分析:
- 匯編:
介紹:
一個有 n 個結點的連通圖的生成樹是原圖的極小連通子圖,且包含原圖中的所有 n 個結點,
并且有保持圖連通的最少的邊。
最小生成樹可以用kruskal(克魯斯卡爾)算法或prim(普里姆)算法求出
普利姆算法,圖論中一種算法,可在加權連通圖里搜索最小生成樹。
此算法搜索到的邊子集所構成的樹中,不但包括連通圖里的所有頂點,且所有邊的權值最小
代碼:
#include <stdio.h>
#include <stdlib.h>/*
程序描述:
矩陣有多行數據,cost數組從矩陣中提取數據,P記錄cost數組的數據分別屬于矩陣的哪一行
Mark記錄在cost不再進行比較數據的下標(已經是最小值當前cost中最小值的下標了)
在cost數組中找出最小值與其在cost中的下標,再將該下標在mark中標記,下次不再處理這個位置
當前cost比較完成后,用找到的最小值作為下一行要提取數據的行號,然后用該行的數據與cost中的數據
比較,取每個位置較小值,除了已經標記的位置不進行提取。并修改P中對應較小值屬于行
更新cost和P后,再進行在cost中找最小值同樣的操作,依次循環整個矩陣
*/#define VNUM 9
#define MV 65536int P[VNUM];//存儲要當前比較的數據是屬于哪一行的
int Cost[VNUM];//要用于比較的數據的數組
int Mark[VNUM];//記錄列狀態,標記為1的列,將不再處理比較
int Matrix[VNUM][VNUM] = //n行與n列數據一樣的矩陣
{{0, 10, MV, MV, MV, 11, MV, MV, MV},{10, 0, 18, MV, MV, MV, 16, MV, 12},{MV, 18, 0, 22, MV, MV, MV, MV, 8},{MV, MV, 22, 0, 20, MV, MV, 16, 21},{MV, MV, MV, 20, 0, 26, MV, 7, MV},{11, MV, MV, MV, 26, 0, 17, MV, MV},{MV, 16, MV, MV, MV, 17, 0, 19, MV},{MV, MV, MV, 16, 7, MV, 19, 0, MV},{MV, 12, 8, 21, MV, MV, MV, MV, 0},
};
//cost 先取第一行的數據開始比較
void Prim(int sv) // O(n*n)
{int i = 0;int j = 0;if( (0 <= sv) && (sv < VNUM) )//判斷sv在矩陣范圍內{for(i=0; i<VNUM; i++){Cost[i] = Matrix[sv][i];//將sv行所有列賦到cost,表示從sv行的數據開始處理比較P[i] = sv;//將P全部賦0,表示當前所有數據屬于0行的Mark[i] = 0;//Mark數組全賦0,初始化}Mark[sv] = 1;//將0列設為1,剛開始0列不處理比較for(i=0; i<VNUM; i++){int min = MV;int index = -1;for(j=0; j<VNUM; j++){//從沒有被標記數據中取值,找出cost(當前要比較的數據)中最小值和其在cost中的下標if( !Mark[j] && (Cost[j] < min) ){min = Cost[j];//給最小值賦值 index = j;//最小值的下標 }}if( index > -1 )//表示執行了上面,找到了最小值{Mark[index] = 1; //將該下標進行標記,下次不再比較該列的數據printf("(%d, %d, %d)\n", P[index], index, Cost[index]); // 輸出這次查找出最小值位于的行與下標與數值}for(j=0; j<VNUM; j++) //循環找出下一次用比較的數據{//從上次找到的最小值的下標,作為重新提取數據的行//只要不是被標記的列,從行中提取的數據比原來比較的數據小就取行中的數和下標//也用新的一行中的數據與本來用于比較的數據取對應位置較小的一方,并將該位置的值屬于//哪一行中提取出來的,存到P中if( !Mark[j] && (Matrix[index][j] < Cost[j]) ) //更新到cost數組{Cost[j] = Matrix[index][j];//更新用來比較數據數組P[j] = index;//更新數據屬于的行}}}}
}int main(int argc, char *argv[])
{Prim(0);getchar();return 0;
}分析:





匯編:
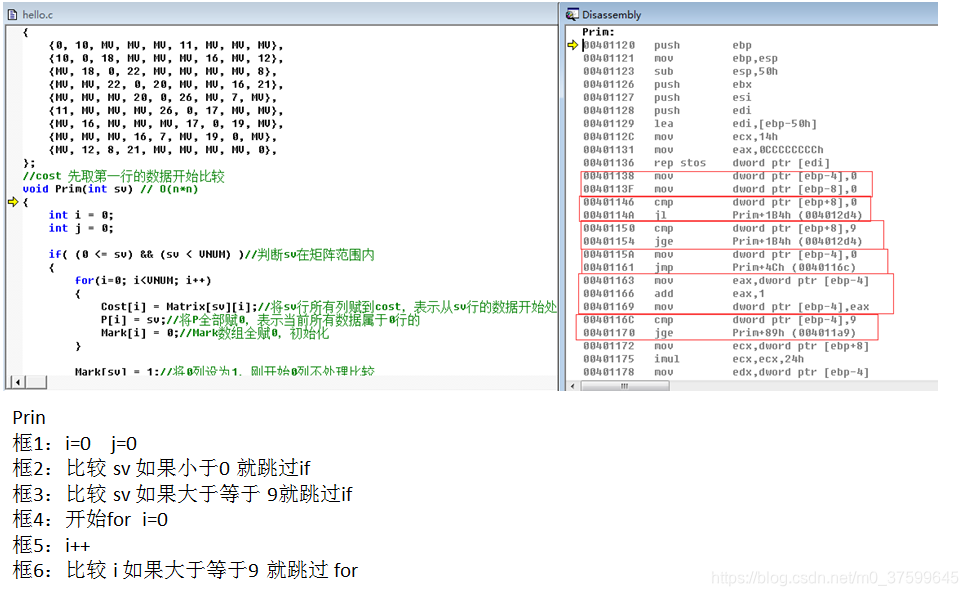
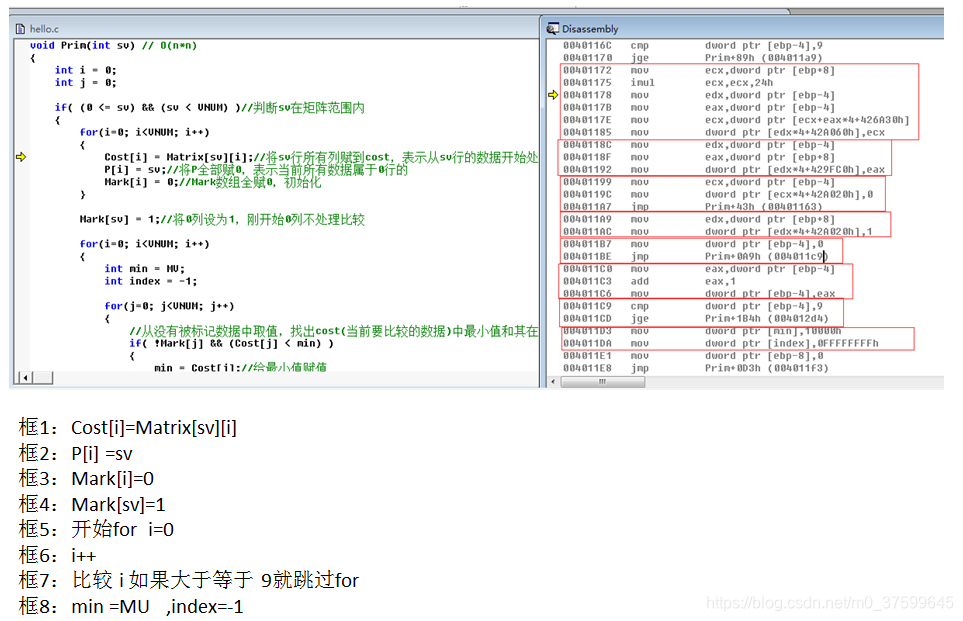
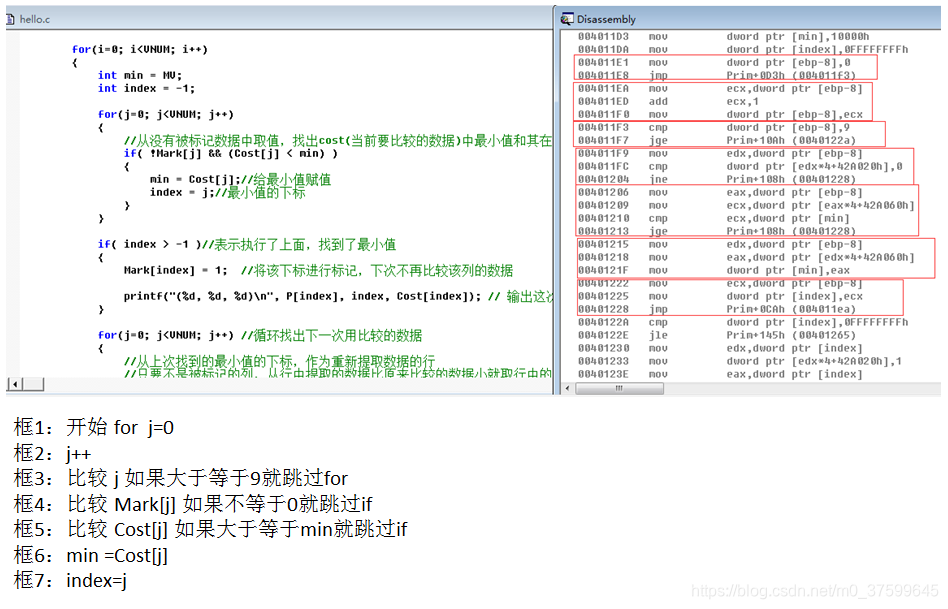
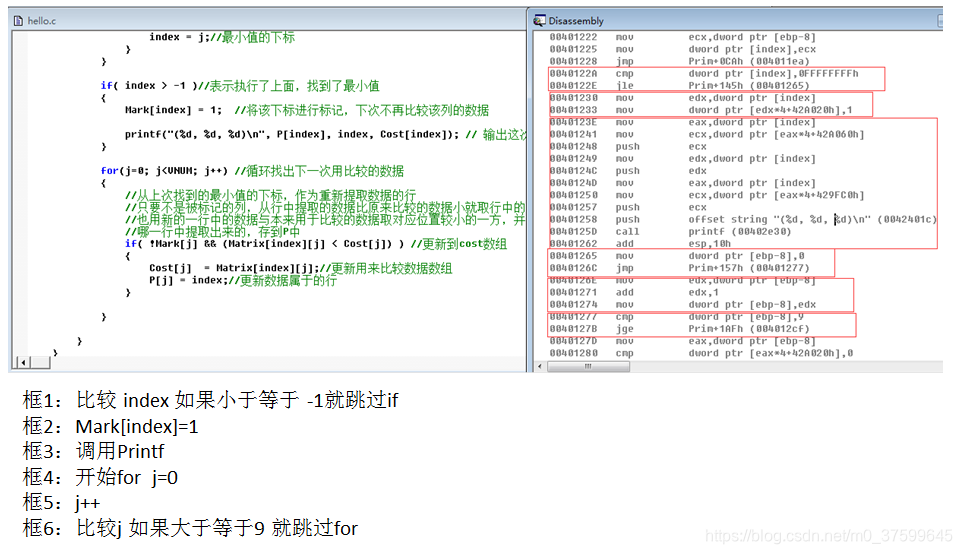
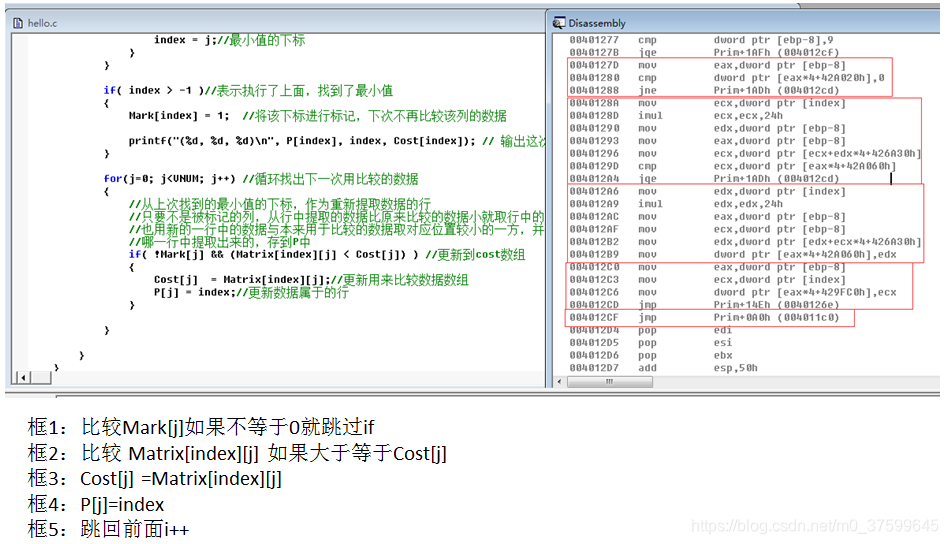

...)


方法及示例)
)
 又稱為二叉查找樹(Binary Search Tree) - (代碼、分析))



方法與示例)

)

方法與示例)



——常用操作)
