目錄
- 【1】NN復雜度
- 【2】指數衰減學習率
- 【3】激活函數
- 優秀激活函數所具有的特點
- 常見的激活函數
- 對于初學者的建議
- 【4】損失函數
- 【5】緩解過擬合——正則化
- 【6】參數優化器
- 【1】SGD
- 【2】SGDM(SGD基礎上增加了一階動量)
- 【3】Adagrade(SGD基礎上增加了二階動量)
- 【4】RMSProp(SGD基礎上增加了二階動量)
- 【5】Adam(同時結合SGDM一階動量和RMSProp的二節動量)
- 優化器對比總結
【1】NN復雜度
空間復雜度:
層數:隱藏層層數+輸出層
總參數:總w+總b
時間復雜度:
乘加運算次數
以下圖為例:總參數=3x4+4(第一層) +4x2+2(第二層)=26
乘加運算次數=3x4+4x2=20

【2】指數衰減學習率
已知:學習率過小,收斂速度慢。學習率過大導致不收斂。
可以先用較大的學習率,快速得到較優解,然后逐步減小學習率,使模型在訓練后期穩定,例如指數衰減學習率。
指數衰減學習率=初始學習率*學習率衰減率^(當前輪數/多少輪衰減一次)
epoch = 40
LR_BASE = 0.2 # 最初學習率
LR_DECAY = 0.99 # 學習率衰減率
LR_STEP = 1 # 喂入多少輪BATCH_SIZE后,更新一次學習率
for epoch in range(epoch): # for epoch 定義頂層循環,表示對數據集循環epoch次,此例數據集數據僅有1個w,初始化時候constant賦值為5,循環100次迭代。lr = LR_BASE * LR_DECAY ** (epoch / LR_STEP)
【3】激活函數

對于線性函數,即使有多個神經元首尾相接構成深層神經網絡,依舊是線性組合,模型表達力不夠。

MP模型比簡化模型多了一個激活函數,它的加入加強了模型的表達力,使得深層網絡不再是輸入x的線性組合,而且隨著層數增加提升表達力。
優秀激活函數所具有的特點
非線性:激活函數非線性時,多層神經網絡可以逼近所有函數
可微性:優化器大多用梯度下降更新參數
單調性:當激活函數是單調的,能保證單層網絡的損失函數是凸函數
近似恒等性:f(x)約等于x,當參數初始化為隨機小值時,神經網絡更穩定激活函數輸出值的范圍:
1、激活函數輸出為有限值時,權重對于特征的影響會更顯著,基于梯度的優化方法更穩定
2、激活函數輸出為無限值時,參數的初始值對模型的影響特別大,要使用更小的學習率
常見的激活函數
1、sigmoid函數:
函數公式、函數圖像與導數圖像:
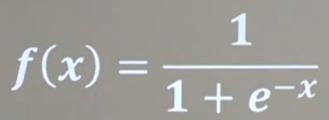 |  |
調用方法:tf.nn.sigmoid(x)
特點:
1、易造成梯度消失(輸入的值較大時,梯度就約等于0了)
2、輸出非0均值,收斂慢(我們希望輸入每層網絡的特征是以0為均值的小數)
3、冪運算復雜,訓練時間長
神經網絡最初興起的時候,sigmoid函數作為激活函數用的很多,但是近年來用sigmoid函數的網絡已經很少了。
因為,深層神經網絡更新參數時,需要從輸出層到輸入層逐層進行鏈式求導,而sigmoid函數導數的輸出范圍是(0,0.25],鏈式求導需要多層導數連續相乘,這樣最終導致輸出為0,造成梯度消失,參數無法繼續更新。
2、Tanh函數:
調用方法:tf.math.tanh(x)
特點:
1、易造成梯度消失
2、輸出0均值
3、冪運算復雜,訓練時間長
函數公式、函數圖像與導數圖像:
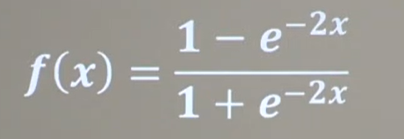 |  |
3、Relu函數:
函數公式、函數圖像與導數圖像:
 |  |
送入激活函數的輸入特征是負數時,激活函數輸出是0,反向傳輸梯度是0,經過relu函數的負數特征過多導致神經元死亡,我們可以改進隨機初始化,避免過多負數特征傳入,也可以通過設置更小的學習率,減少參數分布的巨大變化,避免訓練中產生過多負數特征
4、Leaky Relu函數:
函數公式、函數圖像與導數圖像:
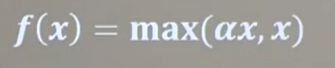 |  |
調用方法:tf.nn.leaky_relu(x)
理論上來說,leaky relu具有relu的所有優點,外加不會有deadrelu問題,但是在實際操作中,并沒有完全證明leaky relu總好于relu
對于初學者的建議
1、首選relu激活函數
2、學習率設置較小值
3、輸入特征標準化,讓輸入特征滿足以0為均值,1為標準差的正態分布
4、初始參數中心化,讓隨機生成的參數滿足0位均值,sqrt(2/當前層輸入特征個數)為標準差的正態分布
【4】損失函數
NN優化目標:loss最小
常用三種損失函數:1、mse(均方差)2、自定義3、ce(交叉熵)
1、mse(均方差)
mse調用方式:
loss_mse =tf.reduce_mean(tf.square(y_-y))
預測酸奶代碼:
import tensorflow as tf
import numpy as npSEED = 23455rdm = np.random.RandomState(seed=SEED) # 生成[0,1)之間的隨機數
x = rdm.rand(32, 2)
y_ = [[x1 + x2 + (rdm.rand() / 10.0 - 0.05)] for (x1, x2) in x] # 生成噪聲[0,1)/10=[0,0.1); [0,0.1)-0.05=[-0.05,0.05)
x = tf.cast(x, dtype=tf.float32)w1 = tf.Variable(tf.random.normal([2, 1], stddev=1, seed=1))epoch = 15000
lr = 0.002for epoch in range(epoch):with tf.GradientTape() as tape:y = tf.matmul(x, w1)loss_mse = tf.reduce_mean(tf.square(y_ - y))grads = tape.gradient(loss_mse, w1)w1.assign_sub(lr * grads)if epoch % 500 == 0:print("After %d training steps,w1 is " % (epoch))print(w1.numpy(), "\n")
print("Final w1 is: ", w1.numpy())
生成的系數確實約等于1
2、自定義損失函數
以銷量預測為例:
均方誤差損失函數默認認為銷量預測多了、少了,造成的損失是一樣的,其實不然。
預測多了:損失成本
預測少了:損失利潤
若利潤不等于成本,則mse產生的loss無法利益最大化!
可以把損失定義為一個分段函數
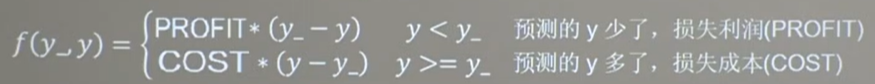
loss_zdy=tf,reduce_sum(tf.where(tf.greater(y,y_),COST(y-y_),PROFIT(y_-y)))
如:預測酸奶銷量,酸奶成本(COST)1元,酸奶利潤(PROFIT)99元。
預測少了損失利潤99元,大于預測多了損失成本1元。
預測少了損失大,希望生成的預測函數往多了預測。
預測酸奶代碼:(修改損失函數)
import tensorflow as tf
import numpy as npSEED = 23455
COST = 1
PROFIT = 99rdm = np.random.RandomState(SEED)
x = rdm.rand(32, 2)
y_ = [[x1 + x2 + (rdm.rand() / 10.0 - 0.05)] for (x1, x2) in x] # 生成噪聲[0,1)/10=[0,0.1); [0,0.1)-0.05=[-0.05,0.05)
x = tf.cast(x, dtype=tf.float32)w1 = tf.Variable(tf.random.normal([2, 1], stddev=1, seed=1))epoch = 10000
lr = 0.002for epoch in range(epoch):with tf.GradientTape() as tape:y = tf.matmul(x, w1)loss = tf.reduce_sum(tf.where(tf.greater(y, y_), (y - y_) * COST, (y_ - y) * PROFIT))grads = tape.gradient(loss, w1)w1.assign_sub(lr * grads)if epoch % 500 == 0:print("After %d training steps,w1 is " % (epoch))print(w1.numpy(), "\n")
print("Final w1 is: ", w1.numpy())# 自定義損失函數
# 酸奶成本1元, 酸奶利潤99元
# 成本很低,利潤很高,人們希望多預測些,生成模型系數大于1,往多了預測
生成的系數確實都大于1
3、ce(交叉熵)
調用方式:tf.losses.categorical_crossentropy(y_, y)
import tensorflow as tfloss_ce1 = tf.losses.categorical_crossentropy([1, 0], [0.6, 0.4])
loss_ce2 = tf.losses.categorical_crossentropy([1, 0], [0.8, 0.2])
print("loss_ce1:", loss_ce1)
print("loss_ce2:", loss_ce2)# 交叉熵損失函數
一般來說,輸出先通過softmax函數使之符合概率分布,再計算y與y_的交叉熵損失函數,TensorFlow提供了同時計算的函數
tf.nn.softmax_cross_entropy_with_logits(y_, y)
# softmax與交叉熵損失函數的結合
import tensorflow as tf
import numpy as npy_ = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1], [1, 0, 0], [0, 1, 0]])
y = np.array([[12, 3, 2], [3, 10, 1], [1, 2, 5], [4, 6.5, 1.2], [3, 6, 1]])
y_pro = tf.nn.softmax(y)
loss_ce1 = tf.losses.categorical_crossentropy(y_,y_pro)
loss_ce2 = tf.nn.softmax_cross_entropy_with_logits(y_, y)print('分步計算的結果:\n', loss_ce1)
print('結合計算的結果:\n', loss_ce2)
【5】緩解過擬合——正則化
為什么正則化可以化解過擬合,先看看下面兩個視頻和講解吧:
過擬合
正則化如何運行
正則化不舍棄特征,而是減少了特征變量的量級,從而簡化假設模型。由于變量過多,我們事先并不知曉每個變量對結果的相關程度,也就是說我們不知道該縮小哪些參數,我們選擇縮小所有參數,也就是給所有參數加上懲罰項(除了theta0變量)。
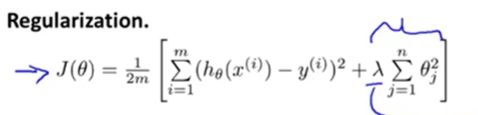
正則化參數λ用來控制兩個不同目標之間的取舍:
1、更好地擬合訓練數據
2、保持參數盡量地小
λ過大同樣也會造成欠擬合的現象。
欠擬合解決方法:
1、增加輸入特征項
2、增加網絡參數
3、減少正則化參數
過擬合的解決方法:
1、數據清洗
2、增大訓練集
3、采用正則化
4、增大正則化參數

示例:利用神經網絡區分藍色點和紅色點

思路:
1、先用神經網絡擬合出數據x1,x2,y_c的函數關系
2、生成網格覆蓋這些點
3、將網格中坐標送入訓練好的神經網絡
4、網絡為每個坐標輸出一個預測值
5、將神經網絡輸出為0.5的預測值的線標出顏色,這線就是區分線
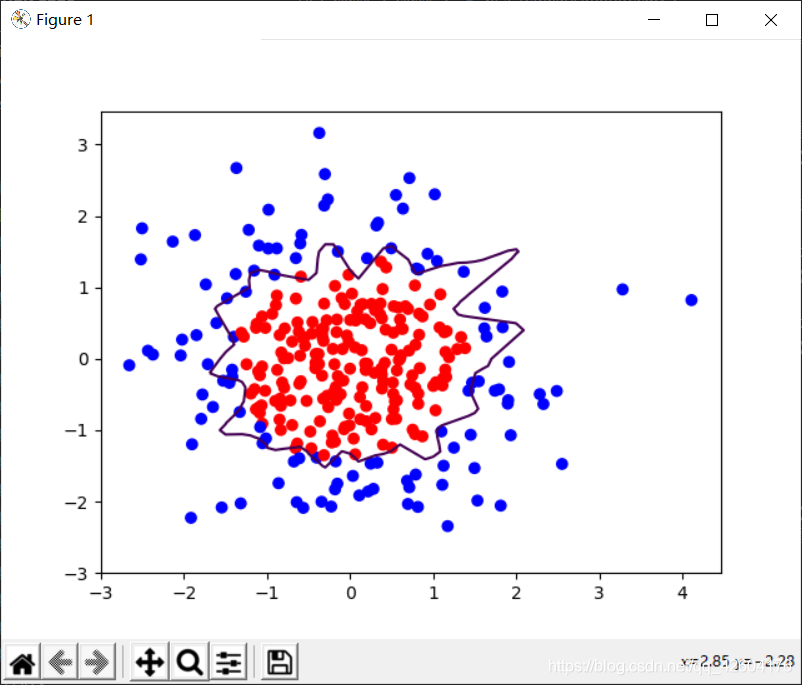
分別輸出不正則化和正則化的效果,觀察效果
左側是正則化之前的,右側是正則化之后的。
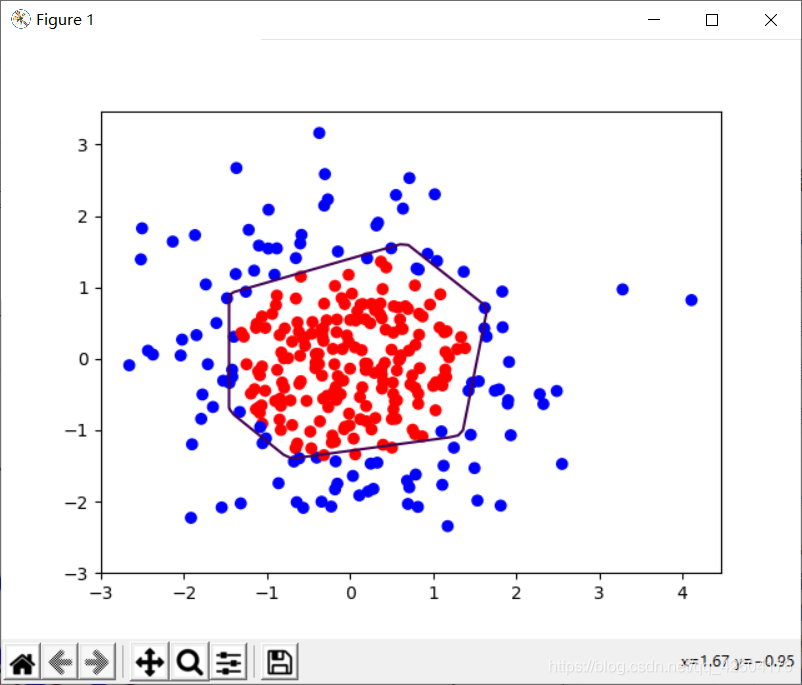 1層隱藏層,4個神經元 1層隱藏層,4個神經元 | 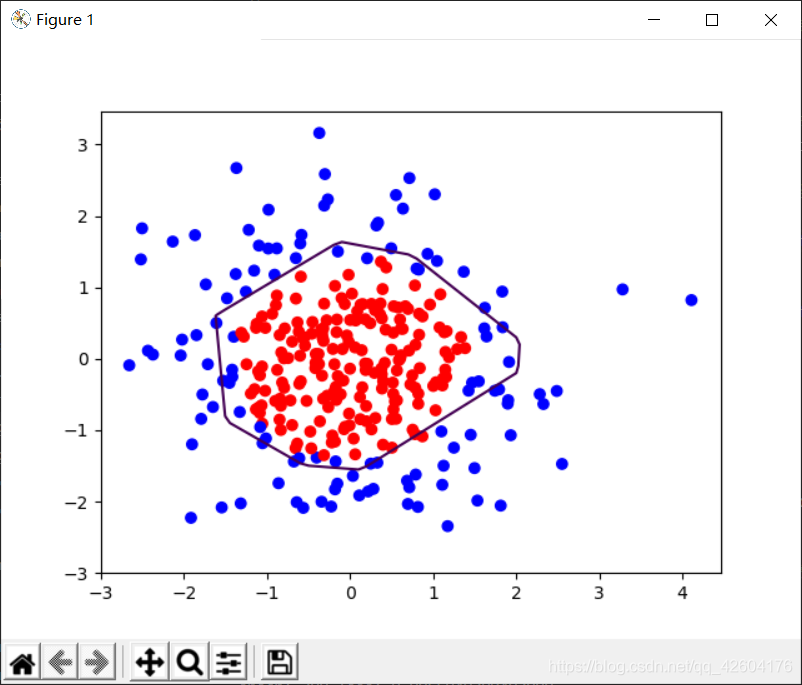 1層隱藏層,4個神經元 1層隱藏層,4個神經元 |
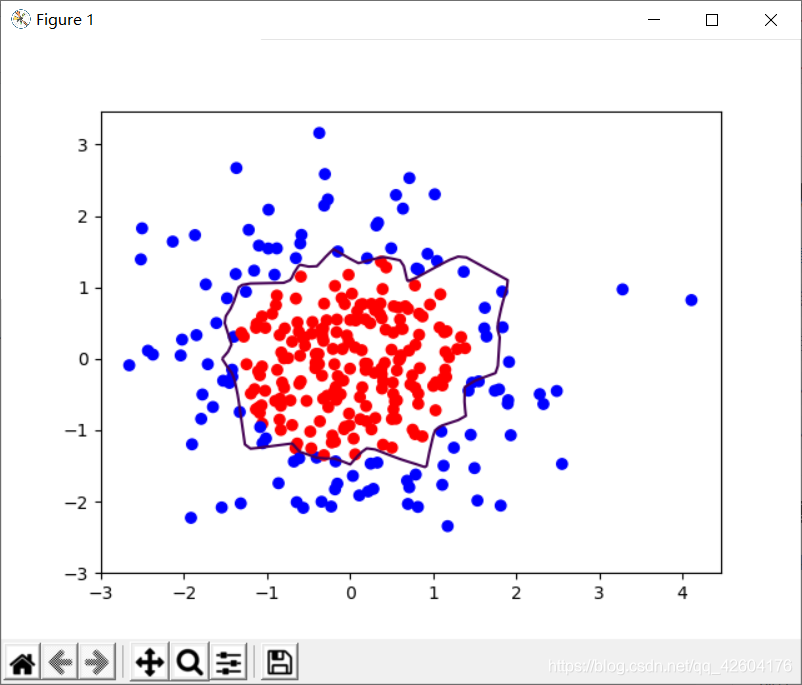 1層隱藏層,22個神經元 1層隱藏層,22個神經元 | 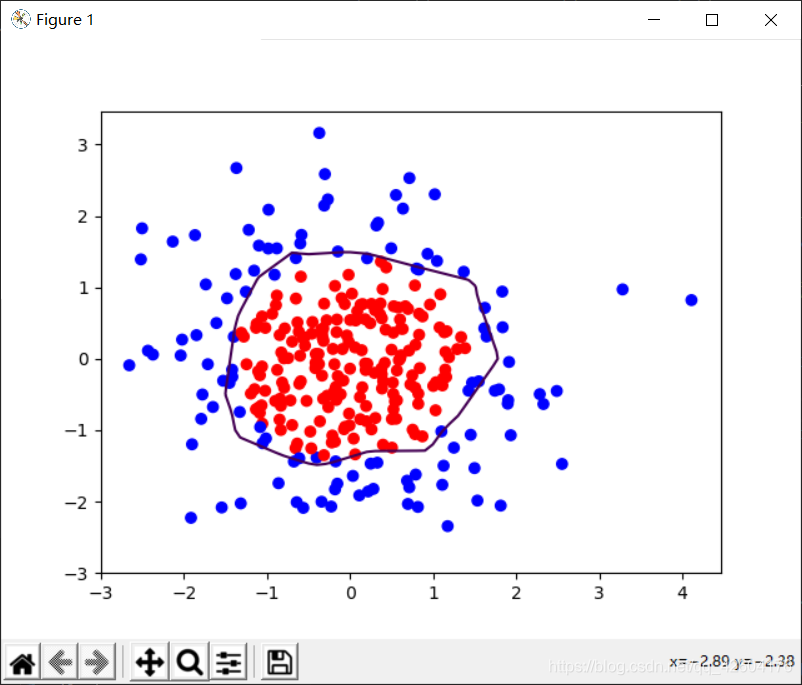 1層隱藏層,22個神經元 1層隱藏層,22個神經元 |
 1層隱藏層,40個神經元 1層隱藏層,40個神經元 | 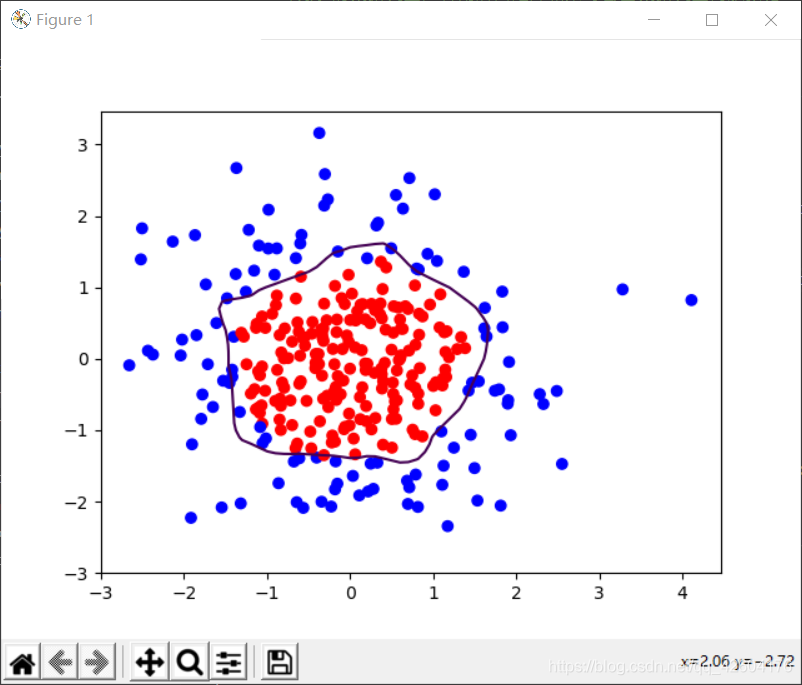 1層隱藏層,40個神經元 1層隱藏層,40個神經元 |
很明顯地可以看出,加入L2正則化后的曲線更加平緩。有效緩解了過擬合。
【6】參數優化器
推薦鏈接
【基礎算法】神經網絡參數優化器https://zhuanlan.zhihu.com/p/97873519
MOOC神經網絡參數優化器
參數優化器總體公式:

【1】SGD
公式: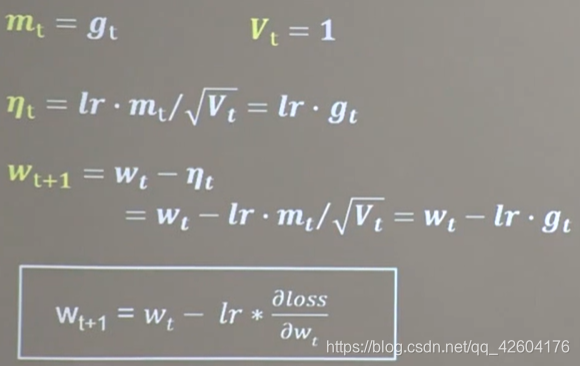
code:
# 實現梯度更新 w1 = w1 - lr * w1_grad b = b - lr * b_grad
w1.assign_sub(lr * grads[0]) # 參數w1自更新
b1.assign_sub(lr * grads[1]) # 參數b自更新
【2】SGDM(SGD基礎上增加了一階動量)
公式:
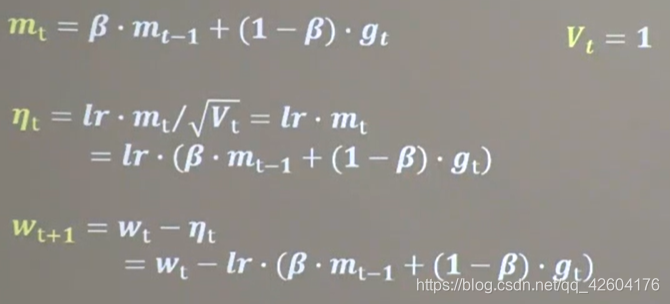
mt表示各時刻梯度方向的指數滑動平均值,表征了過去一段時間的平均值。β是接近1的超參數,一般等于0.9
code:
m_w, m_b = 0, 0
beta = 0.9# sgd-momentun
m_w = beta * m_w + (1 - beta) * grads[0]
m_b = beta * m_b + (1 - beta) * grads[1]
w1.assign_sub(lr * m_w)
b1.assign_sub(lr * m_b)
【3】Adagrade(SGD基礎上增加了二階動量)
公式:
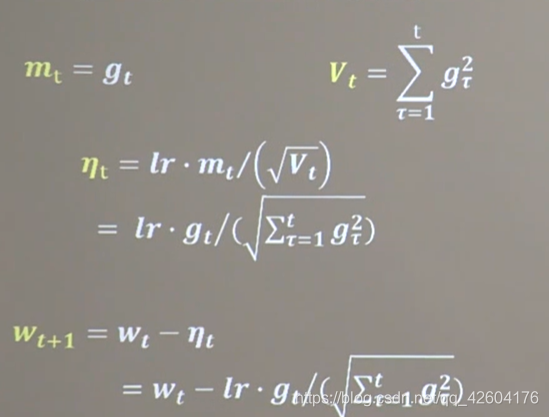
code:
v_w, v_b = 0, 0
# adagrad
v_w += tf.square(grads[0])
v_b += tf.square(grads[1])
w1.assign_sub(lr * grads[0] / tf.sqrt(v_w))
b1.assign_sub(lr * grads[1] / tf.sqrt(v_b))
【4】RMSProp(SGD基礎上增加了二階動量)
公式:
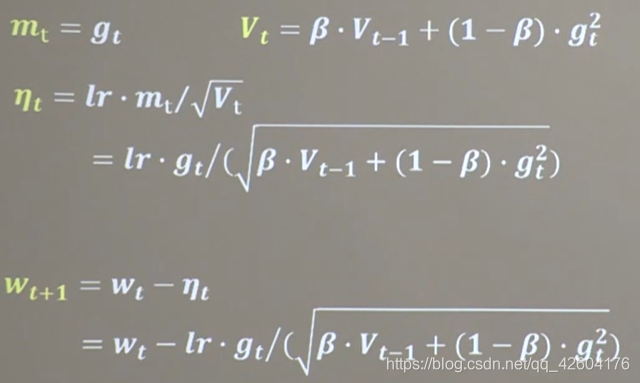
v_w, v_b = 0, 0
beta = 0.9
# rmsprop
v_w = beta * v_w + (1 - beta) * tf.square(grads[0])
v_b = beta * v_b + (1 - beta) * tf.square(grads[1])
w1.assign_sub(lr * grads[0] / tf.sqrt(v_w))
b1.assign_sub(lr * grads[1] / tf.sqrt(v_b))
【5】Adam(同時結合SGDM一階動量和RMSProp的二節動量)
公式:

code:
m_w, m_b = 0, 0
v_w, v_b = 0, 0
beta1, beta2 = 0.9, 0.999
delta_w, delta_b = 0, 0
global_step = 0
# adam
m_w = beta1 * m_w + (1 - beta1) * grads[0]
m_b = beta1 * m_b + (1 - beta1) * grads[1]
v_w = beta2 * v_w + (1 - beta2) * tf.square(grads[0])
v_b = beta2 * v_b + (1 - beta2) * tf.square(grads[1])m_w_correction = m_w / (1 - tf.pow(beta1, int(global_step)))
m_b_correction = m_b / (1 - tf.pow(beta1, int(global_step)))
v_w_correction = v_w / (1 - tf.pow(beta2, int(global_step)))
v_b_correction = v_b / (1 - tf.pow(beta2, int(global_step)))w1.assign_sub(lr * m_w_correction / tf.sqrt(v_w_correction))
b1.assign_sub(lr * m_b_correction / tf.sqrt(v_b_correction))
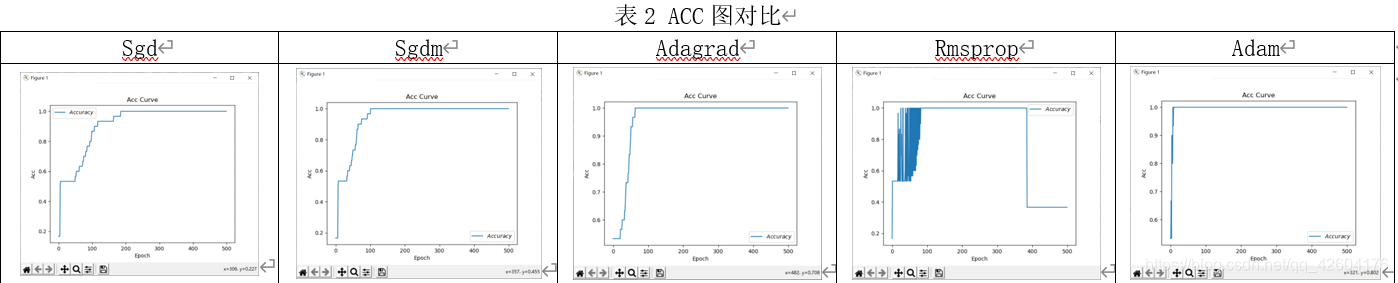
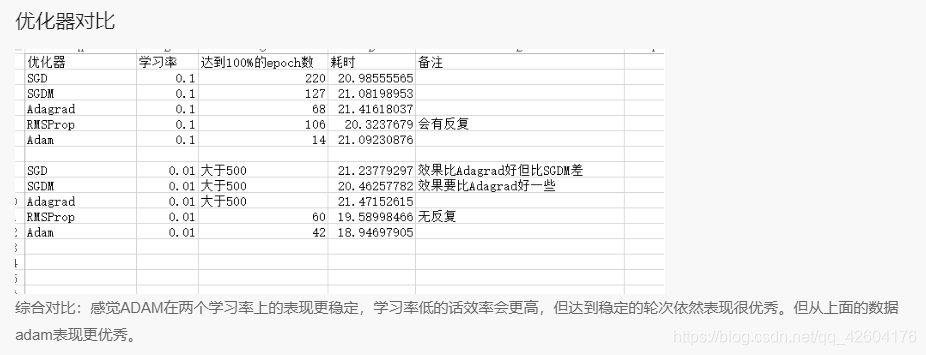
優化器對比總結
優化器對比(lr=0.1 epoch=500 batch=32)







方法)


:項目管理三大目標)



)

方法與示例)


之C語言程序設計復試筆試最后押題五套卷...)

