題目
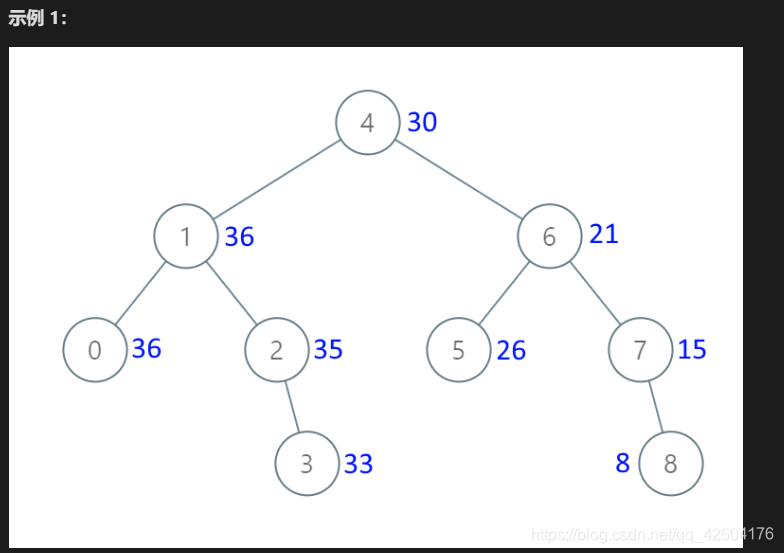
給出二叉 搜索 樹的根節點,該樹的節點值各不相同,請你將其轉換為累加樹(Greater Sum Tree),使每個節點 node 的新值等于原樹中大于或等于 node.val 的值之和。
提醒一下,二叉搜索樹滿足下列約束條件:
節點的左子樹僅包含鍵 小于 節點鍵的節點。
節點的右子樹僅包含鍵 大于 節點鍵的節點。
左右子樹也必須是二叉搜索樹。


遞歸思路
二叉搜索樹的中序遍歷是一個單調遞增的數組,我們要做的就是求出從后到前的累加值:
[2,5,13]->[20,18,13]
數組的從后向前累加轉換成二叉搜索樹就是反中序遍歷,這樣就是按照val單調遞減的順序遍歷了。
依然需要一個pre指針記錄當前遍歷結點cur的前一個結點。
遞歸函數參數以及返回值
遍歷整棵樹,不需要返回值做操作
定義一個全局變量pre,用來保存cur結點的前一個結點的數值,定義為int型就可以了
int pre; //記錄前一個結點的數值
void traversal(TreeNode* cur)
終止條件
遇到空結點就返回
if(cur == NULL) return ;
單層邏輯
按照右中左來遍歷二叉樹,中結點的處理邏輯就是讓cur的數值加上前一個結點的數值
traversal(cur->right); //右
cur->val+=pre;
pre=cur->val;
traversal(cur->left); //左
整體代碼:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int pre; //記錄前一個結點的數值void traversal(TreeNode* cur){if(cur == NULL) return ;traversal(cur->right); //右cur->val+=pre;pre=cur->val;traversal(cur->left); //左}TreeNode* convertBST(TreeNode* root) {pre = 0;traversal(root);return root;}
};
迭代法
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int pre; //記錄前一個結點的數值void traversal(TreeNode* root){stack<TreeNode*> st;TreeNode* cur = root;while(cur!=nullptr || !st.empty()){if(cur != nullptr){st.push(cur);cur = cur->right; //右}else{cur =st.top();st.pop();cur->val+=pre;pre = cur->val;cur = cur->left;}}}TreeNode* convertBST(TreeNode* root) {pre = 0;traversal(root);return root;}
};















及封裝dll實例)



