本文為參考公眾號所做的筆記。
代碼隨想錄原文

回溯法本質是窮舉，窮舉所有可能，然后選出我們想要的答案，所以它并不是一個高效的算法。但是由于有些問題本身能用暴力搜出來就不錯了，所以回溯法也有很多的應用。
回溯法解決的問題
1、組合問題：N個數里面按一定規則找出k個數的集合
2、排列問題：N個數按一定規則全排列，有幾種排列方式
3、切割問題：一個字符串按一定規則有幾種切割方式
4、子集問題：一個N個數的集合里有多少符合條件的子集
5、棋盤問題：N皇后，解數獨
組合與排列區別：
組合是不強調元素順序的，排列是強調元素順序的。
回溯法的理解
回溯法的解空間是一個樹，回溯法解決的是在集合中遞歸查找子集，集合的大小就構成了樹的寬度，遞歸的深度，都構成了樹的深度。

回溯法模板

1、回溯函數返回值以及參數
返回值一般為空。
一般先寫邏輯，然后需要什么參數就填什么參數

void backtracking(參數)

2、回溯函數終止條件
一般來說搜索到樹的葉子結點，就是找到了滿足條件的一個答案，把這個答案存放起來，并結束本層遞歸。

if(終止條件)
{存放結果;return;
}

3、回溯搜索的遍歷過程
集合的大小構成了樹的寬度
遞歸的深度構成了輸的深度
集合大小和孩子的數量是相等的

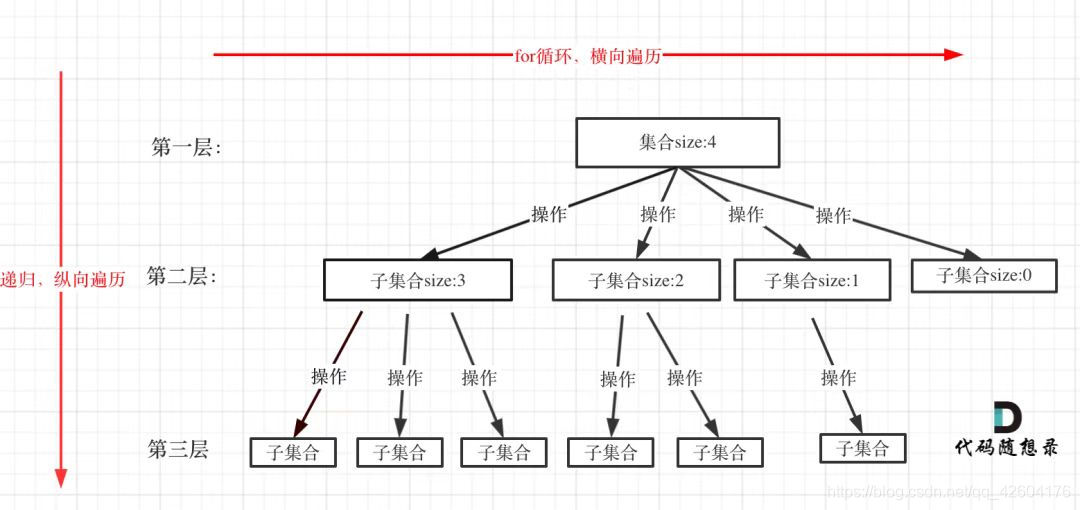
回溯函數遍歷過程的偽代碼如下：

for(選擇：本層集合中的元素（樹中結點孩子的數量就是集合的大小）)
{處理結點;backtracking(路徑,選擇列表);		//遞歸回溯,撤銷處理結果
}

for循環就是遍歷集合區間，可以理解一個結點有多少個孩子，這個for循環就執行多少次。
for循環就是橫向遍歷，backtracking就是縱向遍歷。
整個模板如下：

void backtracking(參數)
{if(終止條件){存放結果;return;}for(選擇：本層集合中元素(樹中結點孩子的數量就是集合的大小)){處理結點;backtracking(路徑,選擇列表);		//遞歸回溯，撤銷處理結果;}
}