1、題目
編寫一個算法來判斷一個數 n 是不是快樂數。
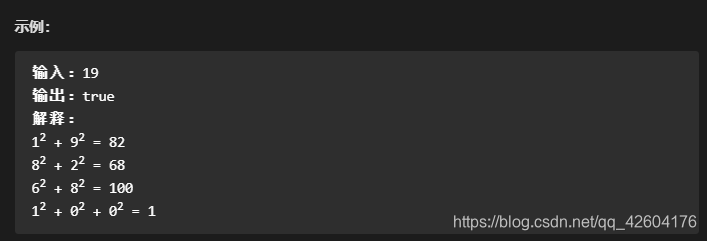
「快樂數」定義為:對于一個正整數,每一次將該數替換為它每個位置上的數字的平方和,然后重復這個過程直到這個數變為 1,也可能是 無限循環 但始終變不到 1。如果 可以變為 1,那么這個數就是快樂數。
如果 n 是快樂數就返回 True ;不是,則返回 False 。
2、思考分析
對一個數不斷進行get_sum操作,那么最終可能的結果有兩種可能:
1、得到1
2、計算的數陷入某種循環,然后會有重復的數出現
如果得到1,直接返回true;
如果檢測到重復數出現就返回false;
否則記錄出現的數,并在while循環中對n進行更新。
int get_sum(int n)
{int sum=0;while(n!=0){sum+=(n%10)*(n%10);n = n/10;}return sum;}
3、哈希法解
class Solution {
public:int get_sum(int n){int sum=0;while(n!=0){sum+=(n%10)*(n%10);n = n/10;}return sum;}bool isHappy(int n) {int sum=0;//sum,sum出現的頻次unordered_set<int> set;while(1){sum=get_sum(n);if(sum ==1) return true;//如果某個數重復出現,那么我們認為此時陷入了循環,則這個數不是快樂數else if(set.find(sum)!=set.end()){return false;}set.insert(sum);n=sum;}}
};
4、雙指針解
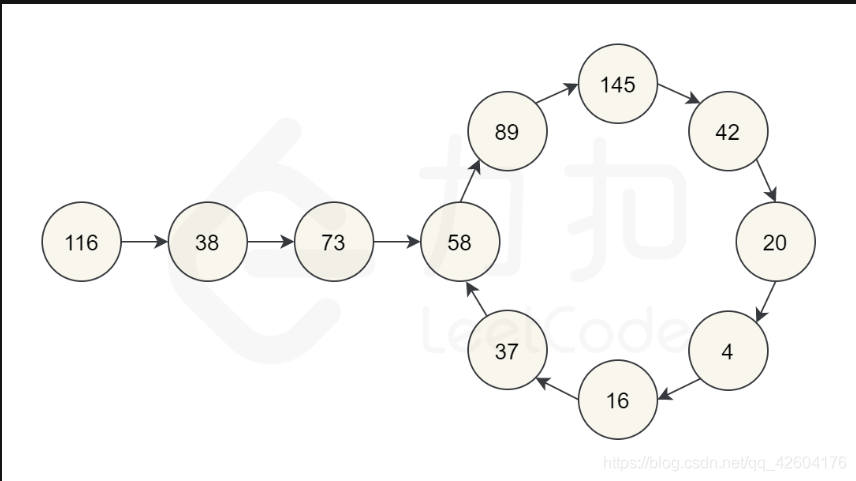
我們得到的結果序列是一個隱式的鏈表。
隱式意味著我們沒有實際的鏈表節點和指針,但數據仍然形成鏈表結構。
于是這個問題可以轉換為檢測一個鏈表是否有環。
這個問題可以使用快慢指針法來解決。我們不是只跟蹤鏈表中的一個值,而是跟蹤兩個值,稱為快跑者和慢跑者。在算法的每一步中,慢速在鏈表中前進 1 個節點,快跑者前進 2 個節點。
前進一次調用一次計算函數,前進兩次調用兩次計算函數。
class Solution {
public:int get_next(int n){int sum=0;while(n!=0){sum+=(n%10)*(n%10);n = n/10;}return sum;}bool isHappy(int n) {int sum=0;int slow_runner = n;int fast_runner = get_next(n);while( fast_runner != 1 && slow_runner != fast_runner){//更新slow_runner,slow_runner每次前進一步slow_runner = get_next(slow_runner);//更新fast_runner,fast_runner每次前進二步,所以調用兩次getnext函數fast_runner = get_next(get_next(fast_runner));}if(fast_runner == 1) return true;return false;}
};


)






---講解)





---小練習)



方法與示例)