博主聯系方式:
QQ:1540984562
QQ交流群:892023501
群里會有往屆的smarters和電賽選手,群里也會不時分享一些有用的資料,有問題可以在群里多問問。
目錄
- 層次分析法的思想
- 層次分析法步驟
- 具體案例(市政工程項目建設決策)
- 1.問題提出
- 2.建立遞階層次結構
- 3.構造判斷矩陣(成對比較陣)并賦值
- 4.層次單排序(計算權向量)與檢驗(一致性檢驗)
- 計算權向量
- 一致性檢驗
- 5.層次總排序(組合權向量)與檢驗(一致性檢驗)
- 6.結果分析
- 7.層次分析法的優缺點
- 層次分析法的代碼實現(matlab)
層次分析法的思想
層次分析法的思想:將所有要分析的問題層次化;
根據問題的性質和所要到達的總目標,將問題分為不同的組成因素,并按照這些因素間的關聯影響即其隸屬關系,將因素按不同層次聚集組合,形成一個多層次分析結構模型;
最后,對問題進行優劣比較排序.
層次分析法步驟
1、找準各因素之間的隸屬度關系,建立遞階層次結構
2、構造判斷矩陣,并賦值
3、層次單排序(計算權向量)與檢驗(一致性檢驗)
4、層次總排序(組合權向量)與檢驗(一致性檢驗)
5、結果分析
具體案例(市政工程項目建設決策)
1.問題提出
市政部門管理人員需要對修建一項市政工程項目進行決策,可選擇的方案是修建通往旅游區的高速路(簡稱建高速路)或修建城區地鐵(簡稱建地鐵)。除了考慮經濟效益外,還要考慮社會效益、環境效益等因素,即是多準則決策問題,考慮運用層次分析法解決。
2.建立遞階層次結構
1、明確決策目標:“合理建設市政工程,使綜合效益最高”。
2、為了實現這一目標,需要考慮的主要準則有三個,即經濟效益、社會效益和環境效益。
還必須考慮直接經濟效益、間接經濟效益、方便日常出行、方便假日出行、減少環境污染、改善城市面貌等因素(準則),從相互關系上分析,這些因素隸屬于主要準則,因此放在下一層次考慮,并且分屬于不同準則。
3、解決方案,即建高速路或建地鐵,這兩個因素作為措施層元素放在遞階層次結構的最下層。
這樣遞階層次就形成了:
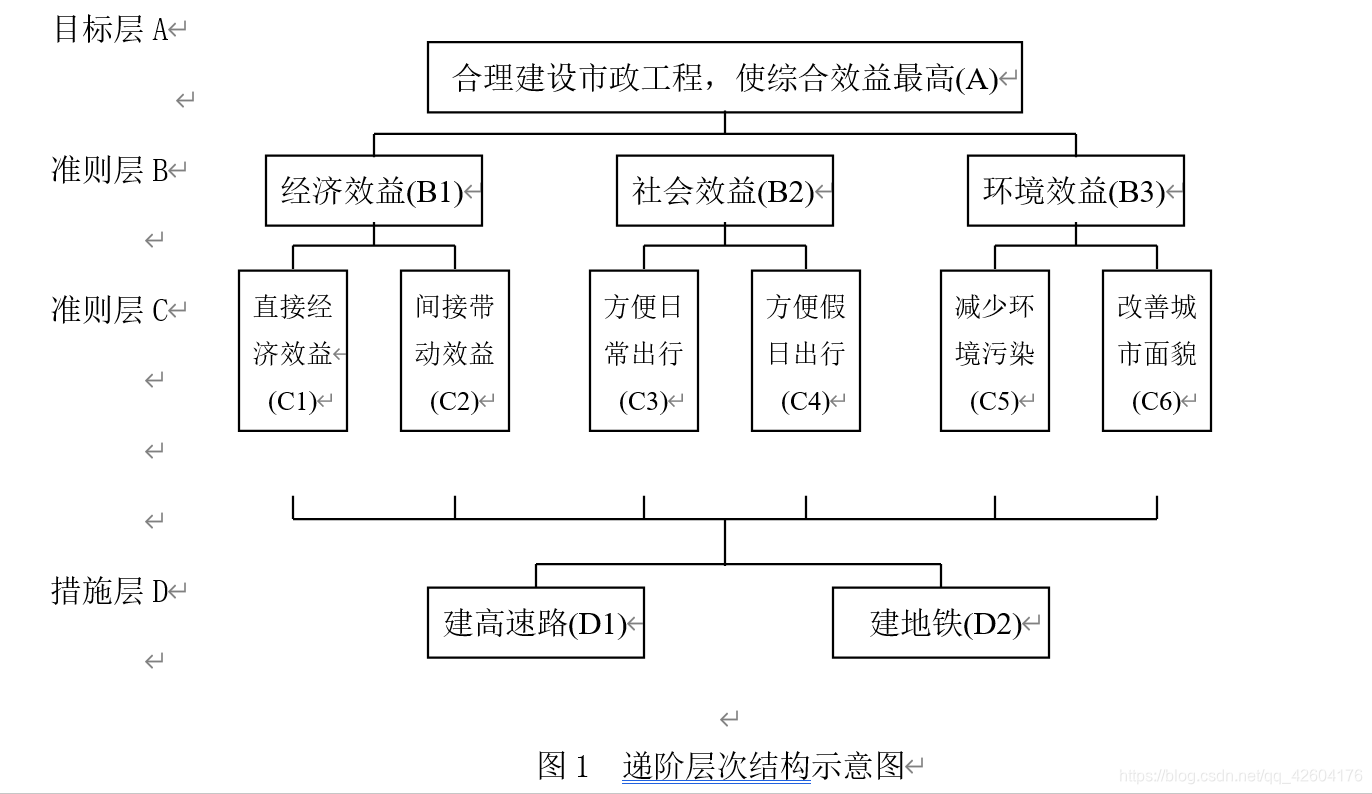
3.構造判斷矩陣(成對比較陣)并賦值
1、構造判斷矩陣的方法:
每一個具有向下隸屬關系的元素(被稱作準則)作為判斷矩陣的第一個元素(位于左上角),隸屬于它的各個元素依次排列在其后的第一行和第一列。
如下圖所示:
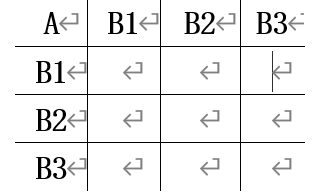
2、如何對判斷矩陣進行賦值:
向填寫人(專家)反復詢問:針對判斷矩陣的準則,其中兩個元素兩兩比較哪個重要,重要多少,對重要性程度按1-9賦值。
(可以類比模糊PID中的隸屬程度,都是人為設定的,也是被人詬病的一個地方)

設填寫后的判斷矩陣為A=(aij)n×n,判斷矩陣具有如下性質:
(1) aij>0
(2) aji=1/ aji
(3) aii=1
判斷矩陣具有對稱性,因此在填寫時,通常先填寫aii=1部分,然后再僅需判斷及填寫上三角形或下三角形的n(n-1)/2個元素就可以了。
在特殊情況下,判斷矩陣可以具有傳遞性,即滿足等式:aij*ajk=aik .
當上式對判斷矩陣所有元素都成立時,則稱該判斷矩陣為一致性矩陣。
對于上述的例子,可以構造出下面的判斷矩陣:

4.層次單排序(計算權向量)與檢驗(一致性檢驗)
計算權向量
對于專家填寫后的判斷矩陣,利用一定數學方法進行層次排序。
層次單排序是指每一個判斷矩陣各因素針對其準則的相對權重,所以本質上是計算權向量。
這里簡要介紹和法:
對于一致性判斷矩陣,每一列歸一化后就是相應的權重。
對于非一致性判斷矩陣,每一列歸一化后近似其相應的權重,在對這n個列向量求取算術平均值作為最后的權重。
公式: 
在層層排序中,要對判斷矩陣進行一致性檢驗。判斷矩陣可以具有傳遞性和一致性。一般情況下,并不要求判斷矩陣嚴格滿足這一性質。
但從人類認識規律看,一個正確的判斷矩陣重要性排序是有一定邏輯規律的,例如若A比B重要,B又比C重要,則從邏輯上講,A應該比C明顯重要,若兩兩比較時出現A比C重要的結果,則該判斷矩陣違反了一致性準則,在邏輯上是不合理的。
因此在實際中要求判斷矩陣滿足大體上的一致性,需進行一致性檢驗。只有通過檢驗,才能說明判斷矩陣在邏輯上是合理的,才能繼續對結果進行分析。
一致性檢驗
第一步,計算一致性指標CI

第二步,查表確定相應的平均隨機一致性指標RI
據判斷矩陣不同階數查下表,得到平均隨機一致性指標RI:
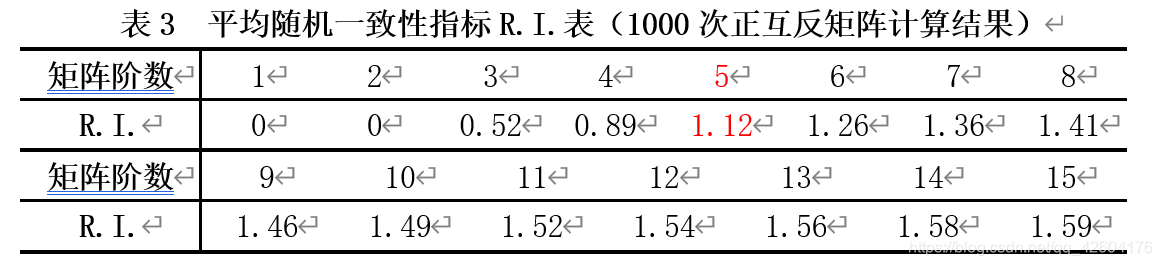
第三步,計算一致性比例CR并進行判斷:
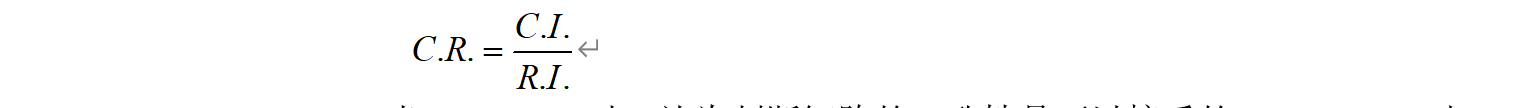
當C.R.<0.1時,認為判斷矩陣的一致性是可以接受的,C.R.>0.1時,認為判斷矩陣不符合一致性要求,需要對該判斷矩陣進行重新修正。
 圖1 圖1 |  圖2 圖2 |
5.層次總排序(組合權向量)與檢驗(一致性檢驗)
總排序是指每一個判斷矩陣各因素針對目標層(最上層)的相對權重。這一權重的計算采用從上而下的方法,逐層合成。
文字性描述公式如下:

計算過程如下,更好理解過程:
P(C1/A) = P(C1/B1) * P(B1/A) = 0.5 * 0.1429 = 0.07145
CR(C1/A) = CR(C/B) * CR(B/A) = 0 * 0 = 0
P(D1/A) = P(D1/C1) * P(C1/B1) * P(B1/A)
+ P(D1/C2) * P(C2/B1) * P(B1/A)
+ P(D1/C3) * P(C3/B2) * P(B2/A)
+ P(D1/C4) * P(C4/B2) * P(B2/A)
+ P(D1/C5) * P(C5/B3) * P(B3/A)
+ P(D1/C6) * P(C6/B3) * P(B3/A)
=0.8333 * 0.5 * 0.1429
+0.75 * 0.5 * 0.1429
+0.1667 * 0.75 * 0.4286
+0.8750 * 0.25 * 0.4286
+0.1667 * 0.75 * 0.4286
+0.8333 * 0.25 * 0.4286
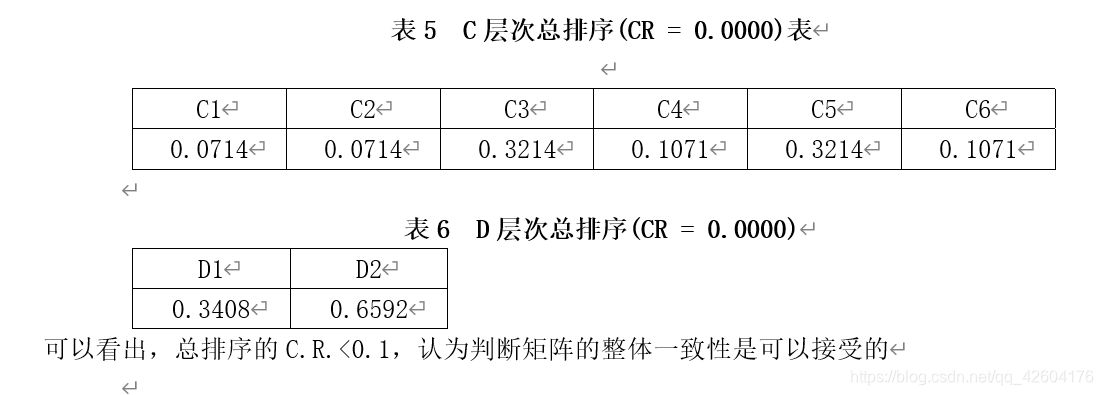
6.結果分析
從方案層總排序的結果看,建地鐵(D2)的權重(0.6592)遠遠大于建高速路(D1)的權重(0.3408),因此,最終的決策方案是建地鐵。
根據層次排序過程分析決策思路:
1、對于準則層B的3個因子,直接經濟效益(B1)的權重最低(0.1429),社會效益(B2)和環境效益(B3)的權重都比較高(皆為0.4286),說明在決策中比較看重社會效益和環境效益。
2、對于不看重的經濟效益,其影響的兩個因子直接經濟效益(C1)、間接帶動效益(C2)單排序權重都是建高速路遠遠大于建地鐵,對于比較看重的社會效益和環境效益,其影響的四個因子中有三個因子的單排序權重都是建地鐵遠遠大于建高速路,由此可以推出,建地鐵方案由于社會效益和環境效益較為突出,權重也會相對突出。
3、從準則層C總排序結果也可以看出,方便日常出行(C3)、減少環境污染(C5)是權重值較大的,而如果單獨考慮這兩個因素,方案排序都是建地鐵遠遠大于建高速路。
由此我們可以分析出決策思路:
即決策比較看重的是社會效益和環境效益,不太看重經濟效益;(總結準則層B)
因此對于具體因子,方便日常出行和減少環境污染成為主要考慮因素,對于這兩個因素,都是建地鐵方案更佳,(總結準則層C)由此,最終的方案選擇建地鐵也就順理成章了。
7.層次分析法的優缺點
優點:
(1)系統性:層次分析把研究對象作為一個系統,按照分解、比較判斷、綜合的思維方式進行決策,成為繼機理分析、統計分析之后發展起來的系統分析的重要工具。
(2)實用性:層次分析把定性和定量方法結合起來,能處理許多許多用傳統的最優化技術無法著手的實際問題,應用范圍很廣。同時,這種方法將決策者和決策分析者相互溝通,決策者甚至可以直接應用它,這就增加了決策者的了解和掌握。
(3)簡潔性:具有中等文化程度的人即可了解層次分析的基本原理和掌握它的基本步驟,計算也非常簡便,并且所得的結果簡單明確,容易為決策者了解和掌握。
缺點:囿舊:只能從原有方案中選優,不能生成新方案;粗略:它的比較、判斷直到結果都是粗糙的,不適于精度要求很高的問題;主觀:從建立層次結構模型到給出成對比較矩陣,人的主觀因素的作用很大,這就使得決策結果可能難以為眾人接受。當然,采取專家群體判斷的辦法是克服這個缺點的一種途徑。
層次分析法的代碼實現(matlab)
disp('請輸入判斷矩陣A(n階)');
A=input('A=');
[n,n]=size(A);
x=ones(n,100);
y=ones(n,100);
m=zeros(1,100);
m(1)=max(x(:,1));
y(:,1)=x(:,1);
x(:,2)=A*y(:,1);
m(2)=max(x(:,2));
y(:,2)=x(:,2)/m(2);
p=0.0001;i=2;k=abs(m(2)-m(1));
while k>pi=i+1;x(:,i)=A*y(:,i-1);m(i)=max(x(:,i));y(:,i)=x(:,i)/m(i);k=abs(m(i)-m(i-1));
end
a=sum(y(:,i));
w=y(:,i)/a;
t=m(i);
disp(w);disp(t);%以下是一致性檢驗
CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];
CR=CI/RI(n);
if CR<0.10disp('此矩陣的一致性可以接受!');disp('CI=');disp(CI);disp('CR=');disp(CR);
end
使用示例:
將上面代碼保存名為test1,并在點運行的時候添加到路徑;
輸入的A矩陣是要以向量的形式輸入的;
之后按下回車即可,可以看到和之前的第4步得到的結果是一樣的。

通過不斷的使用這個式子計算相應矩陣(準則層B到準則層C、準則層C到方案層D)的權向量,最后可以得到最終的結果。
簡單的修改上面的程序,傳入參數為矩陣,免得每次都要打。
function w= test1(A)
% disp('請輸入判斷矩陣A(n階)');
% A=input('A=');
[n,n]=size(A);
x=ones(n,100);
y=ones(n,100);
m=zeros(1,100);
m(1)=max(x(:,1));
y(:,1)=x(:,1);
x(:,2)=A*y(:,1);
m(2)=max(x(:,2));
y(:,2)=x(:,2)/m(2);
p=0.0001;i=2;k=abs(m(2)-m(1));
while k>pi=i+1;x(:,i)=A*y(:,i-1);m(i)=max(x(:,i));y(:,i)=x(:,i)/m(i);k=abs(m(i)-m(i-1));
end
a=sum(y(:,i));
w=y(:,i)/a;
t=m(i);
disp(w);disp(t);%以下是一致性檢驗
CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];
CR=CI/RI(n);
if CR<0.10disp('此矩陣的一致性可以接受!');disp('CI=');disp(CI);disp('CR=');disp(CR);
end
輸入:
Array1=[1 1/3 1/3;3 1 1;3 1 1];
Array2=[1 1;1 1];
Array3=[1 3;1/3 1];
Array4=[1 3;1/3 1];
Array5=[1 5;1/5 1];
Array6=[1 3;1/3 1];
Array7=[1 1/5;5 1];
Array8=[1 7;1/7 1];
Array9=[1 1/5;5 1];
Array10=[1 1/3;7 1];A=test1(Array1);
B1=test1(Array2);
B2=test1(Array3);
B3=test1(Array4);
C1=test1(Array5);
C2=test1(Array6);
C3=test1(Array7);
C4=test1(Array8);
C5=test1(Array9);
C6=test1(Array10);
得到相應的矩陣:
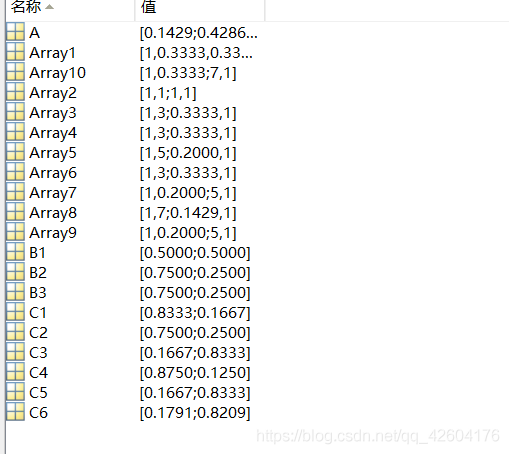


)











)




