目錄
1662. 檢查兩個字符串數組是否相等
題目
自己代碼
5606. 具有給定數值的最小字符串
題目
自己代碼
貪心算法
1664. 生成平衡數組的方案數
題目
自己代碼
動態規劃優化
1665. 完成所有任務的最少初始能量
題目
思路

1662. 檢查兩個字符串數組是否相等

題目

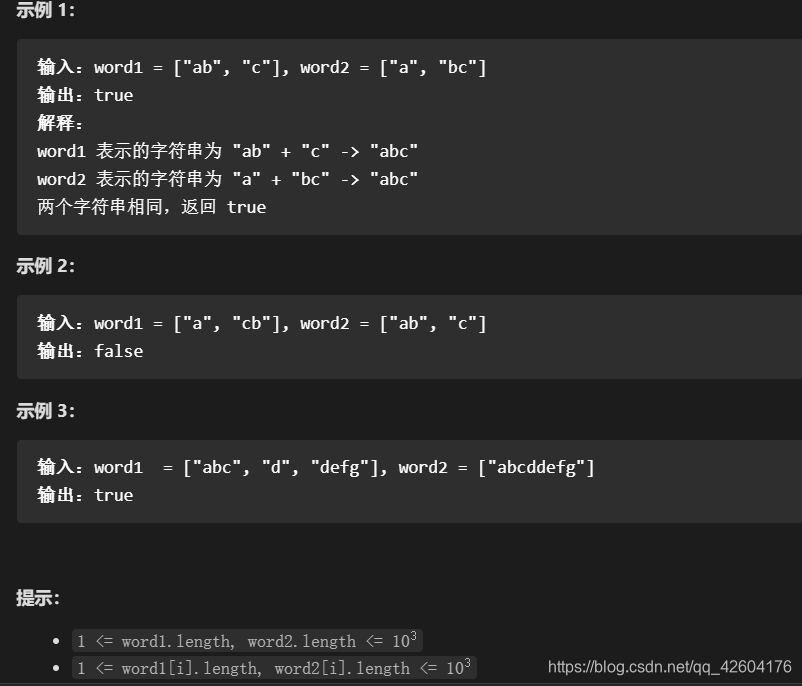
給你兩個字符串數組 word1 和 word2 。如果兩個數組表示的字符串相同，返回 true ；否則，返回 false 。

數組表示的字符串是由數組中的所有元素按順序連接形成的字符串。
在這里插入圖片描述

自己代碼

累加，然后判斷是否相等

class Solution {
public:bool arrayStringsAreEqual(vector<string>& word1, vector<string>& word2) {string str1="";string str2="";for(int i=0;i<word1.size();i++){str1+=word1[i];}for(int i=0;i<word2.size();i++){str2+=word2[i];}if(str1==str2) return true;else return false;}
};

5606. 具有給定數值的最小字符串

題目

小寫字符的數值是它在字母表中的位置（從 1 開始），因此 a 的數值為 1 ，b 的數值為 2 ，c 的數值為 3 ，以此類推。

字符串由若干小寫字符組成，字符串的數值為各字符的數值之和。例如，字符串 “abe” 的數值等于 1 + 2 + 5 = 8 。

給你兩個整數 n 和 k 。返回長度等于 n 且數值等于 k 的字典序最小的字符串。
在這里插入圖片描述

自己代碼

記錄一下自己超時的代碼：
使用的回溯法，這一題使用回溯法并不好，字母越多，解空間樹就會越大，并且沒有使用高效的剪枝手段。
在這里插入圖片描述

class Solution {
public:int sum;int num;string res;char zimu[27]={'a','a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s','t','u','v','w','x','y','z'};bool backtracking(int n,int k){if(num > n || sum > k || (num<n && sum<k && 26*(n-num)<(k-sum))){return false;}//找到了n個數if(num == n && sum == k){return true;}for(int i=1;i<=26;i++){//處理結點；string new_res = res;res+=(zimu[i]);sum+=i;num+=1;//遞歸,探索下一層if(backtracking(n,k)==true) return true;		sum-=i;num-=1;//回溯，撤銷處理結果res=new_res;}return false;}string getSmallestString(int n, int k) {res="";sum=0;num=0;backtracking(n,k);return res;}
};

貪心算法

構造出的字符串字典序最小，可以考慮貪心地從字符串的開頭處開始構造，每次選擇一個滿足要求的最小字母。
假設我們當前構造到了某一個位置，包括此位置還剩下n’個位子沒有放入字符，并且這些位子的數值之和為k’;
那么如果我們放入字母c，那么剩余n’-1個位置以及k’-c的數值和必須滿足：
n’-1<=k’-c<=26(n’-1)
（位置數 <= 位置數上的數值和 <= 位置數能放的最多的數值和）;
這樣就能得到c的取值范圍:
k’ - 26(n’-1) <= c <= k’ - (n’-1)
這樣就能得到c的取值下限k’ - 26(n’-1);
如果下限小于等于0，我們取a(這是我們能取的當中最小的)
如果下限大于0，那么選擇數值對應的字符。
總的來說，就是從第一位到最后一位都取當前能夠取的最小值，這樣就能保證構造出來的字符串字典序最小了。

class Solution {
public:string getSmallestString(int n, int k) {int post_unused=n;int sum_left=k;string result="";while(post_unused!=0){int c=1;if(sum_left - 26*(post_unused-1)<=0)    c=1;else    c=sum_left - 26*(post_unused-1);result+=c-1+'a';post_unused--;sum_left-=c;}return result;}
};

按照這個思路寫一遍。
我他媽傻了，貪心也太牛了，學習了。
在這里插入圖片描述

1664. 生成平衡數組的方案數

題目

給你一個整數數組 nums 。你需要選擇恰好一個下標（下標從 0 開始）并刪除對應的元素。請注意剩下元素的下標可能會因為刪除操作而發生改變。

比方說，如果 nums = [6,1,7,4,1] ，那么：

選擇刪除下標 1 ，剩下的數組為 nums = [6,7,4,1] 。
選擇刪除下標 2 ，剩下的數組為 nums = [6,1,4,1]。
選擇刪除下標 4 ，剩下的數組為 nums = [6,1,7,4] 。
如果一個數組滿足奇數下標元素的和與偶數下標元素的和相等，該數組就是一個平衡數組。

請你返回刪除操作后，剩下的數組 nums 是平衡數組的方案數。
在這里插入圖片描述

自己代碼

又是一個超時代碼
在這里插入圖片描述
先講講思路：
首先nums數組中的每個位置都定義四個相應數組：
分別用來記錄i之前的偶數之和，i之前的奇數之和，i之后的偶數之和，i之后的奇數之和。
然后開始遍歷這個數組，記錄每個位子的四個數組數值。
去除索引為i的元素后，i之前元素的奇偶性不變，i之后元素的奇偶性改變，即i之后奇/偶數下標元素的和變成了偶/奇數下標。
然后暴力解：滿足奇數下標元素的和與偶數下標元素的和相等

class Solution {
public:int waysToMakeFair(vector<int>& nums) {int fangannums=0;for(int i=0;i<nums.size();i++){vector<int> sum={0,0,0,0};for(int j=0;j<i;j+=2){sum[0]+=nums[j];}for(int j=1;j<i;j+=2){sum[1]+=nums[j];}if(i%2==0){for(int j=i+1;j<nums.size();j+=2){sum[2]+=nums[j];}for(int j=i+2;j<nums.size();j+=2){sum[3]+=nums[j];} }else{for(int j=i+1;j<nums.size();j+=2){sum[3]+=nums[j];}for(int j=i+2;j<nums.size();j+=2){sum[2]+=nums[j];} }if(sum[0]+sum[2] == sum[1]+sum[3]) fangannums+=1;}return fangannums;}
};

動態規劃優化

之前超時很明顯就是四個數組值重復計算：i之前的偶數之和，i之前的奇數之和，i之后的偶數之和，i之后的奇數之和。
現在直接看下標，這樣不容易混淆，下標是偶數，數組名字中就有even，下標是奇數，名字中就有odd。
步驟如下：
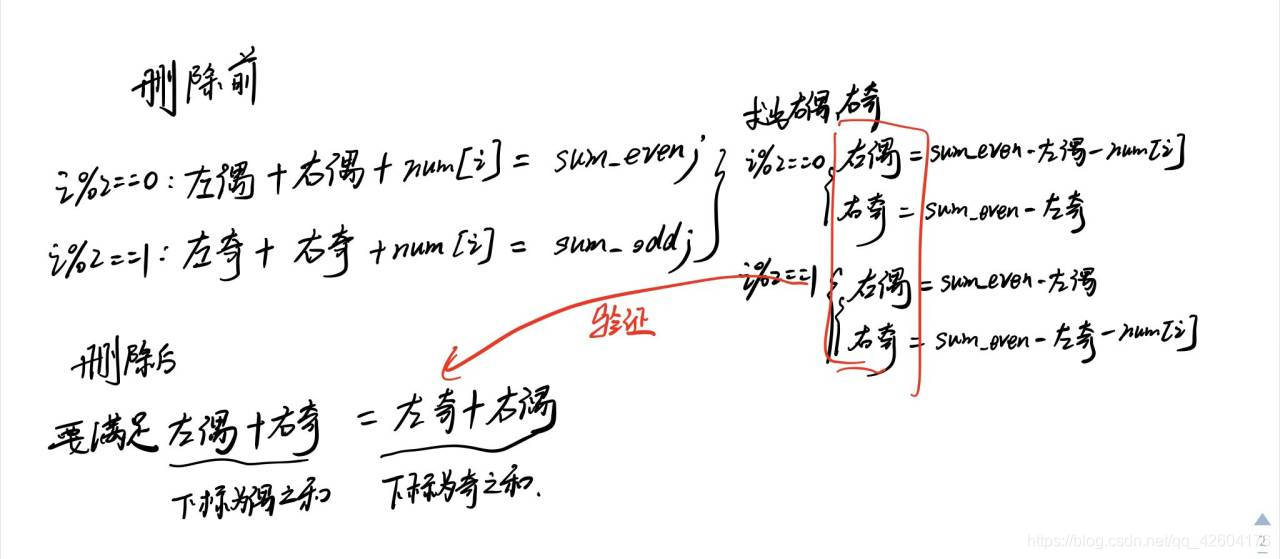
在這里插入圖片描述

在這里插入圖片描述
需要特別注意的地方：
dp推導：
注意這里我們四個數組都不會將nums[i]包括進去的。
i為偶數的話，i-1是奇數，所以左偶和[i] = 左偶和[i-1]，左奇和[i] = 左奇和[i-1]+nums[i-1];
i為奇數的話，i-1是偶數，所以左偶和[i] = 左偶和[i-1]+nums[i-1]，左奇和[i] = 左奇和[i-1];
這樣一來，就能對計算i之前的偶數和，奇數和省下時序。沒必要每次都從i=0開始判斷累加。
其次，i右邊的偶數和，奇數和也沒必要通過for運算開始計算，而是只需要從sum_odd和sum_even中視情況減去左偶右偶、nums[i]即可。
這樣也是同時省下大把時序。

//如果i是偶數下標,i-1為奇數下標
if(i%2==0)  
{before_i_evensum[i]=before_i_evensum[i-1];before_i_oddsum[i]=before_i_oddsum[i-1]+nums[i-1];
}
else
{before_i_evensum[i]=before_i_evensum[i-1]+nums[i-1];before_i_oddsum[i]=before_i_oddsum[i-1];
}

class Solution {
public:int waysToMakeFair(vector<int>& nums) {int fangannums=0;int n = nums.size();//i左邊偶數下標所指數之和vector<int> before_i_evensum(n,0);//i左邊奇數下標所指數之和vector<int> before_i_oddsum(n,0);//i右邊偶數下標所指數之和vector<int> after_i_evensum(n,0);//i右邊偶數下標所指數之和vector<int> after_i_oddsum(n,0);//*******【1】計算數組的奇數下標和以及偶數下標和***//int sum_odd=0;int sum_even=0;for(int i=0;i<n;i++){if(i%2==0) sum_even+=nums[i];else sum_odd+=nums[i];}//****************************************//for(int i=0;i<n;i++){if(i==0){after_i_evensum[0]=sum_even - nums[i];after_i_oddsum[0] = sum_odd; }else{//*******【2】i之前的偶數下標和以及奇數下標和***////如果i是偶數下標,i-1為奇數下標if(i%2==0)  {before_i_evensum[i]=before_i_evensum[i-1];before_i_oddsum[i]=before_i_oddsum[i-1]+nums[i-1];after_i_evensum[i]=sum_even - before_i_evensum[i] - nums[i];after_i_oddsum[i] = sum_odd - before_i_oddsum[i];}//如果i是奇數下標,i-1為偶數下標else{before_i_evensum[i]=before_i_evensum[i-1]+nums[i-1];before_i_oddsum[i]=before_i_oddsum[i-1];after_i_evensum[i]=sum_even - before_i_evensum[i];after_i_oddsum[i] = sum_odd - before_i_oddsum[i] - nums[i];}}if(before_i_evensum[i]+after_i_oddsum[i] == before_i_oddsum[i]+after_i_evensum[i])fangannums++;    }return fangannums;}
};

在這里插入圖片描述
這一題當時并沒有做出來，是剛剛才想到的。

1665. 完成所有任務的最少初始能量

題目

給你一個任務數組 tasks ，其中 tasks[i] = [actuali, minimumi] ：

actuali 是完成第 i 個任務需要耗費的實際能量。
minimumi 是開始第 i 個任務前需要達到的最低能量。
比方說，如果任務為 [10, 12] 且你當前的能量為 11 ，那么你不能開始這個任務。如果你當前的能量為 13 ，你可以完成這個任務，且完成它后剩余能量為 3 。

你可以按照任意順序完成任務。

請你返回完成所有任務的最少初始能量。

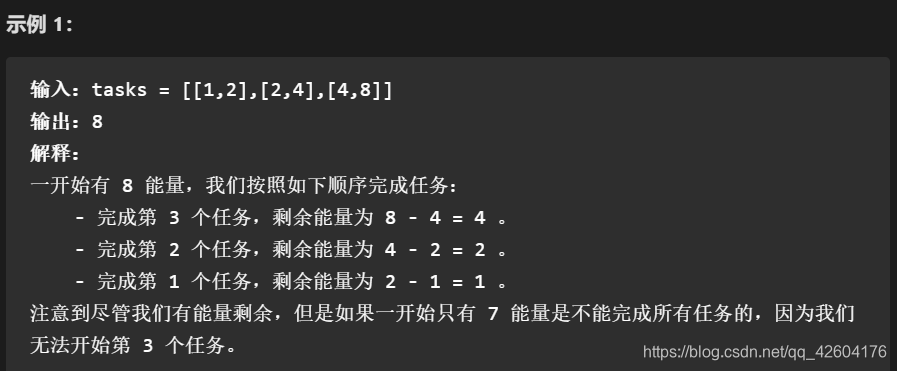
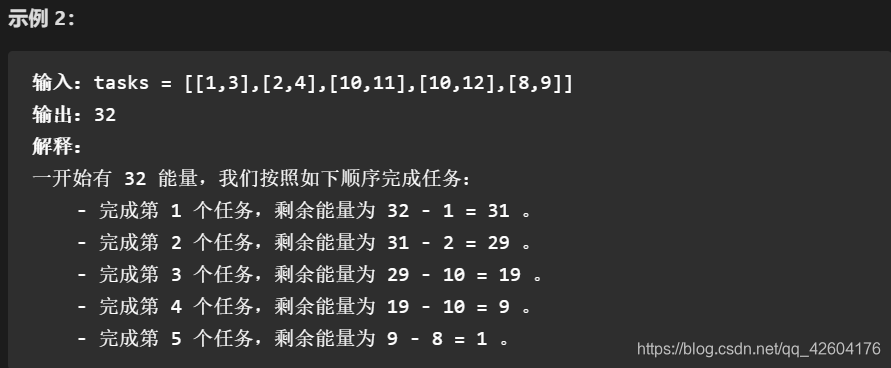
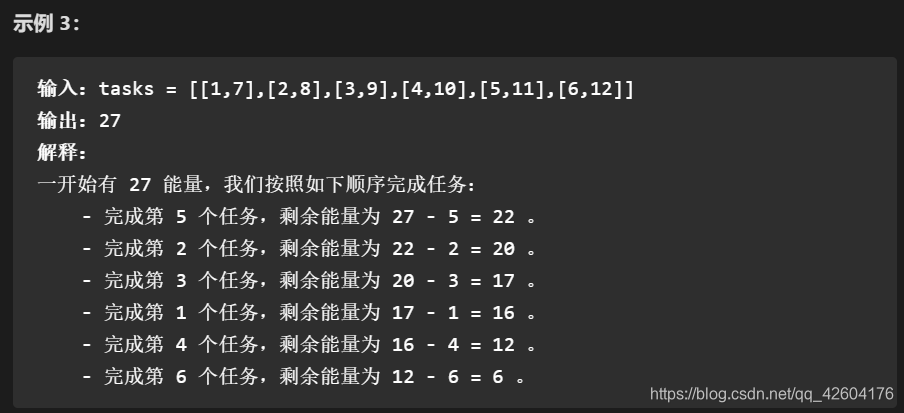
在這里插入圖片描述

思路

觀察示例，可以發現，完成的任務是按照最（低能量-實際能量）的大小來排序的，差越大的越先被執行。
https://leetcode-cn.com/problems/minimum-initial-energy-to-finish-tasks/solution/wan-cheng-suo-you-ren-wu-de-zui-shao-chu-shi-neng-/
神仙題目，這里貼個代碼：

class Solution {
public:static bool cmp(vector<int>& p1, vector<int>& p2) {return p1[1] - p1[0] > p2[1] - p2[0];}int minimumEffort(vector<vector<int>>& tasks) {sort(tasks.begin(), tasks.end(),cmp);int sum=0;  //完成任務需要消耗的實際能量int ans=0;  //完成任務需要達到的最低能量//打印信息// for(auto& task : tasks)// {//     cout<<"task[0]:"<<task[0]<<" task[1]:"<<task[1]<<endl;// }for(auto& task : tasks){//cout<<"ans:"<<ans<<" sum:"<<sum<<endl;ans = max(ans,sum+task[1]);sum +=task[0];}return ans;}
};