目錄

• • 題目
  • 思路分析
  • 代碼
  • 總結

題目

如果連續數字之間的差嚴格地在正數和負數之間交替，則數字序列稱為擺動序列。第一個差（如果存在的話）可能是正數或負數。少于兩個元素的序列也是擺動序列。

例如， [1,7,4,9,2,5] 是一個擺動序列，因為差值 (6,-3,5,-7,3) 是正負交替出現的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是擺動序列，第一個序列是因為它的前兩個差值都是正數，第二個序列是因為它的最后一個差值為零。

給定一個整數序列，返回作為擺動序列的最長子序列的長度。 通過從原始序列中刪除一些（也可以不刪除）元素來獲得子序列，剩下的元素保持其原始順序。

思路分析

畫出序列波動圖：

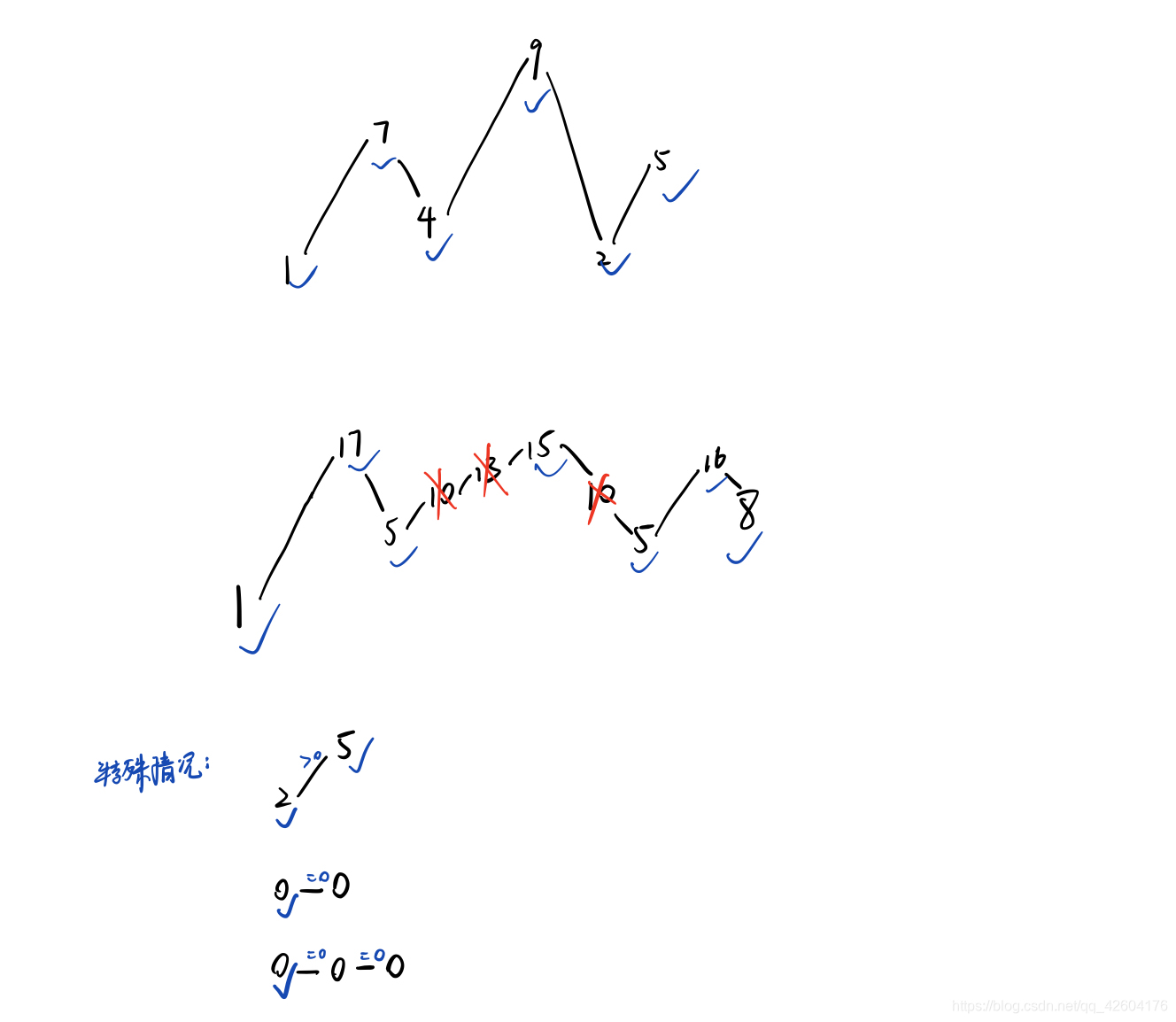
可以發現，我們刪除的是單調遞增或者遞減的坡上的結點(不包括坡頂和坡底)
局部最優：刪除單調坡度上的結點，那么這個坡度就可以有兩個局部峰值
全局最優：整個序列有最多的局部峰值，從而達到最長擺動序列。
實際操作中只需要統計數組中的峰值數量即可。
在實際操作中的時候我們需要用到cur_delta = nums[i] - nums[i-1],pre_delta = nums[i-1] - nums[i-2].
從數組的左端開始，默認序列右端是個峰值。
如果cur_delta >0 && pre_delta <=0 或者 cur_delta <0 && pre_delta >=0,我們認為存在一個峰值。
（因為 pre_delta 被初始化為 0 了，所以這里要加上=號）
并且，只有在存在峰值的時候，我們才更新pre_delta ，因為統計的是峰值，一定是以上一下的，prediff之前是上，接下來就是下

代碼

class Solution {
public:int wiggleMaxLength(vector<int>& nums) {int n = nums.size();if(n<=1) return n;int peak_nums=1;int delta_pre_curr=0;int delta_ppre_pre=0;for(int i = 1;i < n;i++){delta_pre_curr=nums[i]-nums[i-1];if((delta_pre_curr > 0 && delta_ppre_pre <= 0) || (delta_pre_curr < 0 && delta_ppre_pre >= 0)){peak_nums++;delta_ppre_pre=delta_pre_curr;}}return peak_nums;}
};

總結

1.保持區間波動，只需要把單調區間上的元素移除就可以了。
2.因為題目并不需要我們確定最終的序列是什么，所以其實只是要找整個序列單調增/減了幾次。
3.為什么可以將previous diff設置為0是因為他只會在一開始等于0，后面他會被current diff更新，并且如果current diff不滿足嚴格正/負變符號他就不會更新previous diff，所以len(nums)==2不需要單獨拿出來寫幾行代碼
4. res從1開始記錄，因為出發點肯定算一個