目錄

• • 1、題目
  • 2、思路分析
  • 3、參考鏈接

1、題目

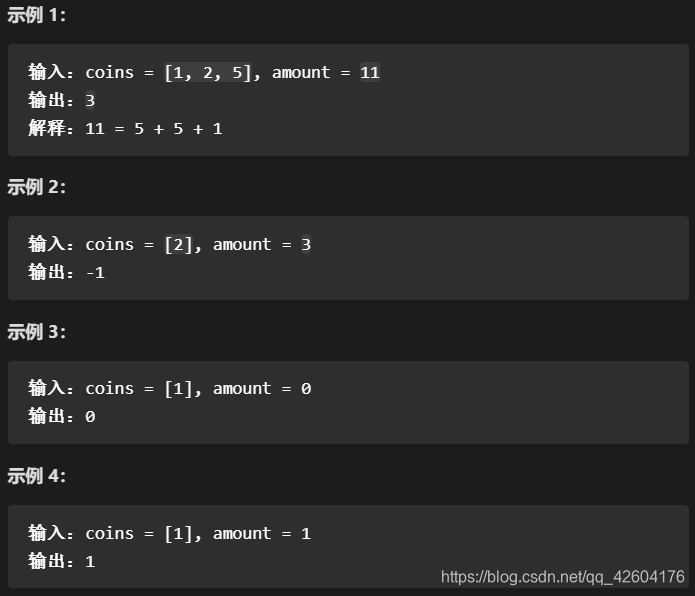
給定不同面額的硬幣 coins 和一個總金額 amount。編寫一個函數來計算可以湊成總金額所需的最少的硬幣個數。如果沒有任何一種硬幣組合能組成總金額，返回 -1。

你可以認為每種硬幣的數量是無限的。

提示：
1 <= coins.length <= 12
1 <= coins[i] <= 231 - 1
0 <= amount <= 104

2、思路分析

這一題和leetcode 39. 組合總和 思考分析有點像，不過要求不同。
39題要求的是所有解的集合，而這一題求的是最優解。
所以直接套用39回溯思路，然后從子解中找到最小的即可，貌似也是能做的，不過會超時。。。

class Solution {
public:int left_sum;int min_coin_nums;int coin_nums;void backtracking(vector<int>& coins,int startindex){   if(left_sum < 0) return;if(left_sum == 0){if(min_coin_nums==0) min_coin_nums=coin_nums;else min_coin_nums=min(min_coin_nums,coin_nums);return;}for(int i=startindex;i<coins.size();i++){if(left_sum-coins[i]<0) break;//處理結點；coin_nums++;left_sum-=coins[i];//遞歸,探索下一層backtracking(coins,i);		//遞歸//回溯，撤銷處理結果left_sum+=coins[i];coin_nums--;}}int coinChange(vector<int>& coins, int amount) {min_coin_nums=0;coin_nums=0;left_sum=amount;//排序加速剪枝sort(coins.begin(),coins.end());backtracking(coins,0);if((min_coin_nums ==0 && amount == 0)||(min_coin_nums != 0)) return min_coin_nums;return -1;}
};

其實這一題是一道動態規劃題：
如果想求amount = 11時的最少硬幣數(原問題)，如果知道amout =10的最少硬幣數(子問題)，你只需要把子問題的答案加一(再選一枚1元的硬幣)，因為硬幣的數量是沒有限制的，當然也可能是amout =6的最少硬幣數加上一個面額為5的硬幣。這時候就需要取最少的硬幣數了。
子問題之間是相互獨立的。
1、分析最優子結構:
湊成面值為 11 的最少硬幣個數可以由以下三者的最小值得到：

湊成面值為 10 的最少硬幣個數 + 面值為 1 的這一枚硬幣；
湊成面值為 9 的最少硬幣個數 + 面值為 2 的這一枚硬幣；
湊成面值為 6 的最少硬幣個數 + 面值為 5 的這一枚硬幣。
dp[11] = min (dp[10] + 1, dp[9] + 1, dp[6] + 1)

2、確定【DP狀態】
dp[i] ：湊齊總價值 i 需要的最少硬幣個數；
3、確定狀態轉移方程

for(int i = 0;i < coins.size();i++)
{if (coin[i] <= amount)dp[amount] = min(1 + dp[amount - coin[i]])  }

需要注意的地方：
單枚硬幣的面值首先要小于等于 當前要湊出來的面值。

class Solution {
public:int coinChange(vector<int>& coins, int amount) {int n = coins.size();//對dp數組中每個值先賦一個不可能的值，因為要比較的是最小值，這個不可能的值就得賦值成為一個最大值，這里只需要比總金額大就行了，表示湊不出來//dp[i] ：湊齊總價值 i 需要的最少硬幣個數；vector<int> dp(amount + 1,amount+1);//湊總金額為0，不需要硬幣dp[0] = 0;//從0到amount，計算湊齊總價值 i 需要的最少硬幣個數；for(int i = 0;i <=amount;i++){//從0到coins.size()，遍歷每個面額的硬幣for(int j = 0;j < n;j++){//總價值必須比該硬幣面額大//并且dp[i - coins[j]]必須被賦過值，也就是說必須有個方案，要能夠湊出來，這樣才能進行下一步推導if(i - coins[j] >= 0 && dp[i - coins[j]] != amount+1){//如果滿足這個條件，那么dp[i]就是dp[i]和當前方案中的最小值，因為dp[i]可能被多次賦值，我們取的是最優值dp[i] = min(dp[i],1 + dp[i - coins[j]]);}}}//dp[amount]沒有沒賦值，說明沒有組合方案，所以應該返回-1if(dp[amount] == amount+1){return -1;}return dp[amount];}};

時間復雜度：O(N \times amount)O(N×amount)，這里 NN 是可選硬幣的種類數，amountamount 是題目輸入的面值；
空間復雜度：O(amount)O(amount)，狀態數組的大小為 amountamount。
由于dp數組是自底向上求解的，所以過程中不會出現重疊子問題
需要注意的地方：

1、數組初始化把初值amount+1換成Integer.MAX_VALUE為什么就不行了 ？
如果初值賦值為正無窮，dp[i - coin] +1 可能會發生整型溢出。
2、循環的判斷條件if (i - coin >= 0 && dp[i - coin] != amount + 1)為什么要判斷 dp[i - coin] != amount + 1呢
amount + 1 在這里表示的是當前狀態表示的金額不能被候選硬幣的和表示。
去掉dp[i-coin] != amount + 1 這個判斷條件也是可以的， 因為若是 dp[i-coin] = amount + 1， 在下一步 dp[i] = Math.min(dp[i], 1 + dp[i - coin]) 也會將amount+1+1這個值過濾掉的，即amount + 1仍然是無效的。 因為數組中的有效值不會超過amount+1，就算有1塊錢的硬幣，最大值也就是amount，因此在取兩個數的最小值時已經自動將amount+1這個值過濾掉了。

3、參考鏈接

動態規劃、完全背包、BFS（包含完全背包問題公式推導）
labuladong的公眾號文章