題目

給定一個非負整數數組，你最初位于數組的第一個位置。

數組中的每個元素代表你在該位置可以跳躍的最大長度。

判斷你是否能夠到達最后一個位置。

示例1：

輸入: [2,3,1,1,4]
輸出: true
解釋: 我們可以先跳 1 步，從位置 0 到達 位置 1, 然后再從位置 1 跳 3 步到達最后一個位置。

示例2：

輸入: [3,2,1,0,4]
輸出: false
解釋: 無論怎樣，你總會到達索引為 3 的位置。但該位置的最大跳躍長度是 0 ， 所以你永遠不可能到達最后一個位置。

思考

這個題目，需要注意每個元素代表你在該位置可以跳躍的最大長度，而不是長度。也就是說如果是3，那么你可以走0，1，2，3步。
其次，觀察題目，不能到達最后一格的原因是：某一格元素為0，且之前沒有足夠步數跨越這個0
來分析一下示例2：[3,2,1,0,4]，連續的0個數為1
我們先遍歷，找到元素0，下標為3。此刻從它前面的一個元素開始往前遍歷：
下標為2的元素為1，步數為1，（步數 - （連續0的第一個下標 - 當前下標 - 1）） =（1 - （3-2 -1））=1 <= 連續的0個數,所以不行
下標為1的元素為2，步數為2，（步數 - （連續0的第一個下標 - 當前下標 - 1）） =（2 - （3-1 -1））=1 <= 連續的0個數,所以不行
下標為0的元素為3，步數為3，（步數 - （連續0的第一個下標 - 當前下標 - 1）） =（3 - （3-0 -1））=1 <= 連續的0個數,所以不行

所以我們可以歸納出一個明顯的特征：（步數 - （連續0的第一個下標 - 當前下標 - 1））> 連續的0個數
只有滿足這個特征才算是可以到達最后一個位置。
代碼實現的時候還需要考慮特殊情況以及細節：
1、長度為1，直接為true
2、遍歷從 i=1開始，i= nums.size()-1,結束
3、獲取連續0的個數：

int succesive_zero = 0;
if(nums[i] == 0)
{succesive_zero = 1;for(int j = i;j < nums.size()-2;j++){if(nums[j] == 0 && nums[j+1] == 0) succesive_zero++;else break;}
}

4、如果找到了可以可以跨越連續0的步數，那么將i指針移動到跳躍的格子。并且，如果在連續0之前沒有找到足夠大的步數跳躍，則說明不能到達最后一個格子，但是找到了，還需要遍歷之后的情況，直到整個數組都被遍歷了，且沒有出現不能跳過的情況，我們才能返回true。

int flag = 0;
for(int j = i-1;j >= 0;j--)
{if((nums[j]-(i-j-1)) > succesive_zero){i=i+succesive_zero;flag=1;break;}
}
if(flag == 0) return false;

AC代碼

class Solution {
public:bool canJump(vector<int>& nums) {if(nums.size() == 1) return true;if(nums[0] == 0) return false;for(int i=1;i < nums.size()-1;i++){//如果當前為0，記錄連續0的個數int succesive_zero = 0;if(nums[i] == 0){succesive_zero = 1;for(int j = i;j < nums.size()-2;j++){if(nums[j] == 0 && nums[j+1] == 0) succesive_zero++;else break;}//cout<< "succesive_zero"<<succesive_zero << endl;//判斷i之前有沒有步數，在走到i后還有剩余的步數跳過這個0，說明暫時可以，否則不行int flag = 0;for(int j = i-1;j >= 0;j--){if((nums[j]-(i-j-1)) > succesive_zero){i=i+succesive_zero;flag=1;break;}}if(flag == 0) return false;}}return true;}
};

參考，貪心思路，思路更加直觀，代碼邏輯更加簡單

參考代碼隨想錄的思路：https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA
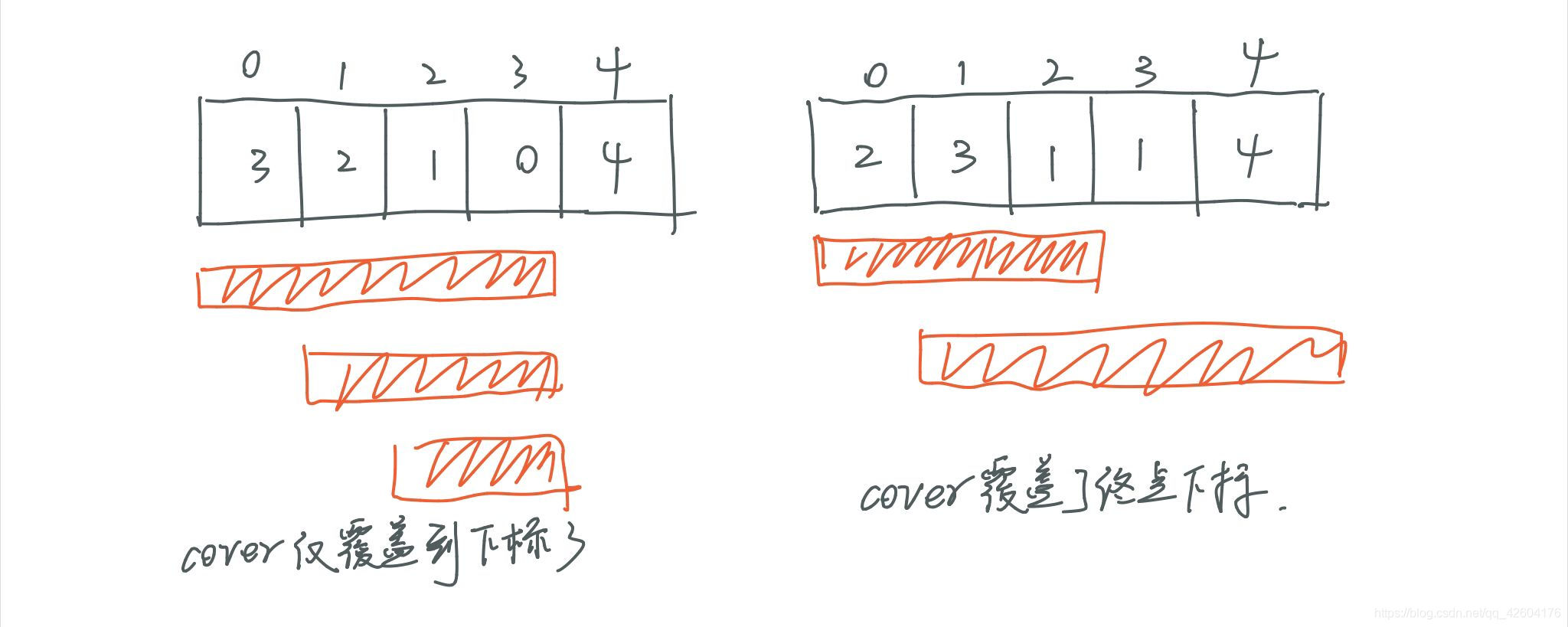
跳幾步無所謂，關鍵在于可跳的范圍：
每次取最大的跳躍步數，這個就是跳躍的覆蓋范圍。
問題轉化為跳躍覆蓋范圍究竟可不可以覆蓋到終點。
每次移動取最大跳躍步數(得到最大覆蓋范圍)，每移動一個單位，就更新最大覆蓋范圍。

**局部最優解：**每次取最大跳躍步數
**整體最優解：**最后得到整體最大覆蓋范圍，看是否能到終點。

編程細節：
1、i只能在cover范圍內移動，每移動一個元素，cover得到該元素數值，補充覆蓋范圍，讓i繼續移動下去。
2、cover每次只取max(鈣元素數值補充后的范圍，cover本身范圍)
3、如果cover >= 終點下標，直接return true；
AC代碼：

class Solution {
public:bool canJump(vector<int>& nums) {//初始化覆蓋范圍int cover = 0;if(nums.size() == 1) return true;//從0開始的覆蓋范圍迭代for(int i = 0; i <= cover;i++){cover = max(i+nums[i],cover);if(cover >= nums.size() - 1) return true; }return false;}
};

有一說一，這個思路確實妙！也很符合貪心的邏輯。