
- 博主簡介:努力學習的22級計算機科學與技術本科生一枚🌸
- 博主主頁: @是瑤瑤子啦
- 每日一言🌼: 所謂自由,不是隨心所欲,而是自我主宰。——康德
目錄
- 一、前言
- 二、刷題
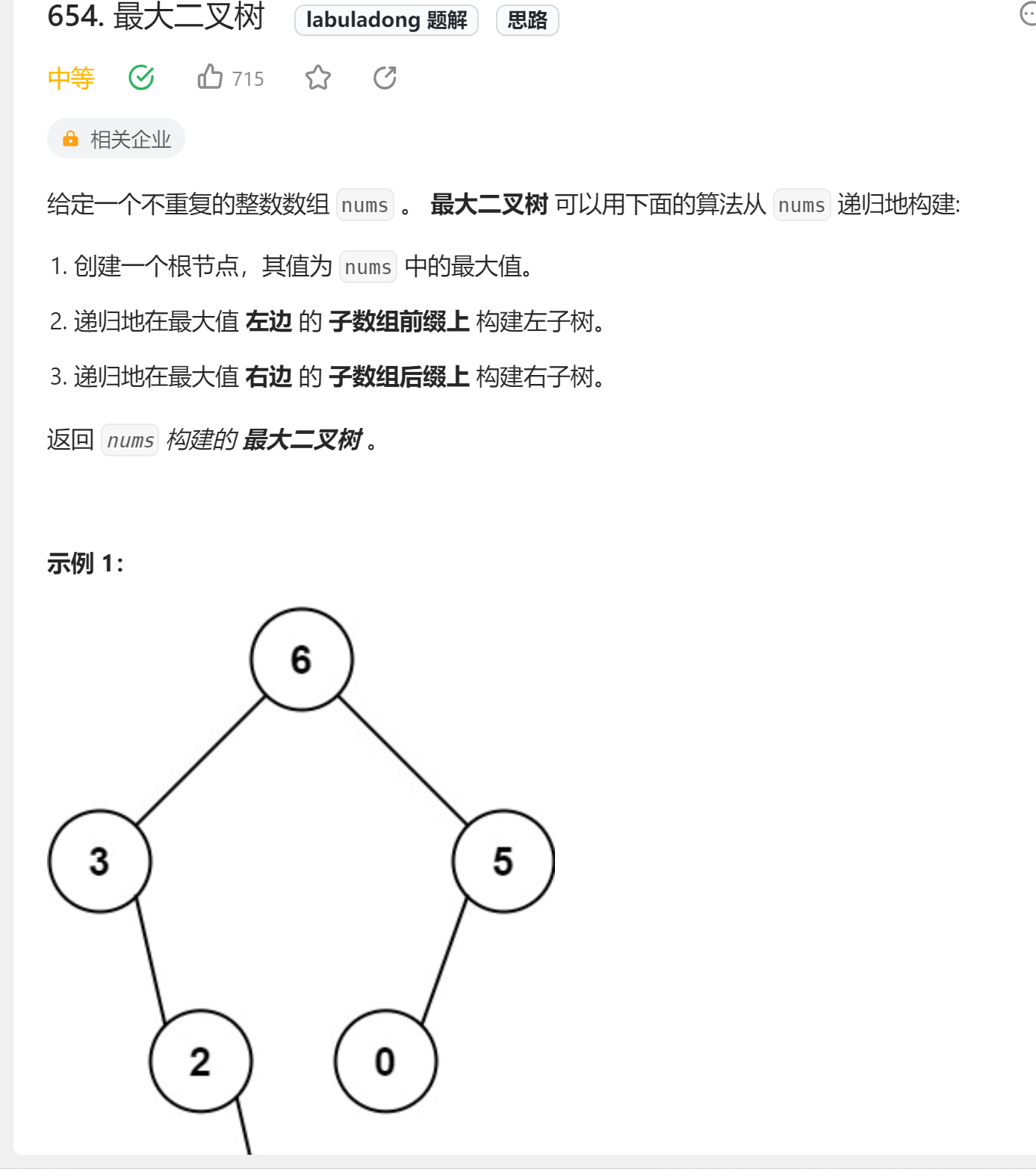
- 1、最大二叉樹
- 2、從前序與中序遍歷序列構造二叉樹
- 3、從中序與后序遍歷序列構造二叉樹
- 4、 根據前序和后序遍歷構造二叉樹
一、前言
🍊 二叉樹的構造問題一般都是使用「分解問題」的思路:構造整棵樹 = 根節點 + 構造左子樹 + 構造右子樹
( 關鍵在于明確遞歸函數的定義,然后利用這個定義,構建二叉樹的套路很簡單,先找到根節點,然后找到并遞歸構造左右子樹即可)
二、刷題
1、最大二叉樹
🔗654. 最大二叉樹
public TreeNode constructMaximumBinaryTree(int[] nums) {if(nums==null||nums.length==0){return null;}//1、找到最大元素,構造根節點int max = nums[0];int index = 0;for (int i = 1; i < nums.length; i++){if(nums[i] > max){index = i;max = nums[i];}}TreeNode root = new TreeNode(max);//左子樹和右子樹數組構造int[] numsLeft = Arrays.copyOfRange(nums, 0, index);int[] numsRight = Arrays.copyOfRange(nums,index+1, nums.length);root.left = constructMaximumBinaryTree(numsLeft);root.right = constructMaximumBinaryTree(numsRight);return root;}
2、從前序與中序遍歷序列構造二叉樹
🔗105. 從前序與中序遍歷序列構造二叉樹
-
👧🏻思路:
- 大的框架還是分解成子問題,這里定義一個遞歸函數:
build(遞歸函數的定義:給定二叉樹前序遍歷、中序遍歷數組、前序數組起始坐標、前序數組末尾坐標、中序數組起始坐標、中序數組末尾坐標) - 在遞歸函數前序位置需要確定左子樹兩個數組的的四個坐標和右子樹的四個坐標,核心是算出當前root在中序數組中的位置
rootIndex
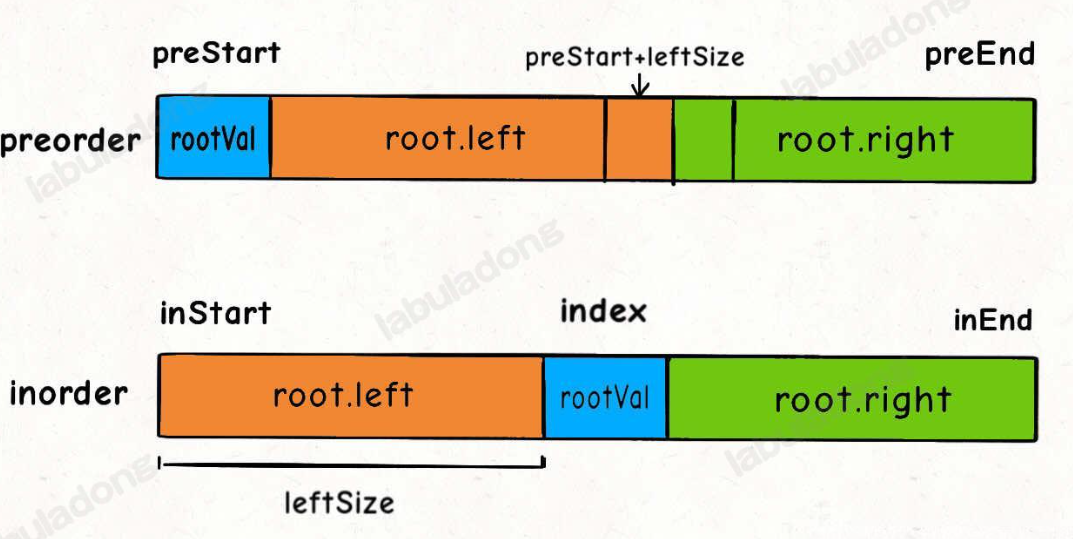
- 大的框架還是分解成子問題,這里定義一個遞歸函數:
-
🙇🏻?♀?代碼:
public TreeNode buildTree(int[] preorder, int[] inorder) {//遞歸函數的定義:給定二叉樹前序遍歷、中序遍歷數組、前序數組起始坐標、前序數組末尾坐標、中序數組起始坐標、中序數組末尾坐標int pStart = 0;int pEnd = preorder.length-1;int iStart = 0;int iEnd = inorder.length-1;return build(preorder,inorder, pStart, pEnd, iStart, iEnd);}public TreeNode build(int[] preorder, int[] inorder, int pStart, int pEnd, int iStart, int iEnd){if(pStart > pEnd){return null;}//1、先在前序數組中找到根節點TreeNode root = new TreeNode(preorder[pStart]);//2、在中序數組中找到根節點,劃分左右數組int rootIndex = -1;int leftSize = 0;for(int i = iStart; i <= iEnd; i++){if(inorder[i] == root.val){rootIndex = i;leftSize = i-iStart;break;}}root.left = build(preorder, inorder, pStart+1, pStart+leftSize, iStart ,rootIndex-1);root.right = build(preorder, inorder, pStart+leftSize+1, pEnd, rootIndex+1, iEnd);return root;}
3、從中序與后序遍歷序列構造二叉樹
🔗106. 從中序與后序遍歷序列構造二叉樹
-
👧🏻思路:
- 同上,關鍵在于四個坐標的確定要準確
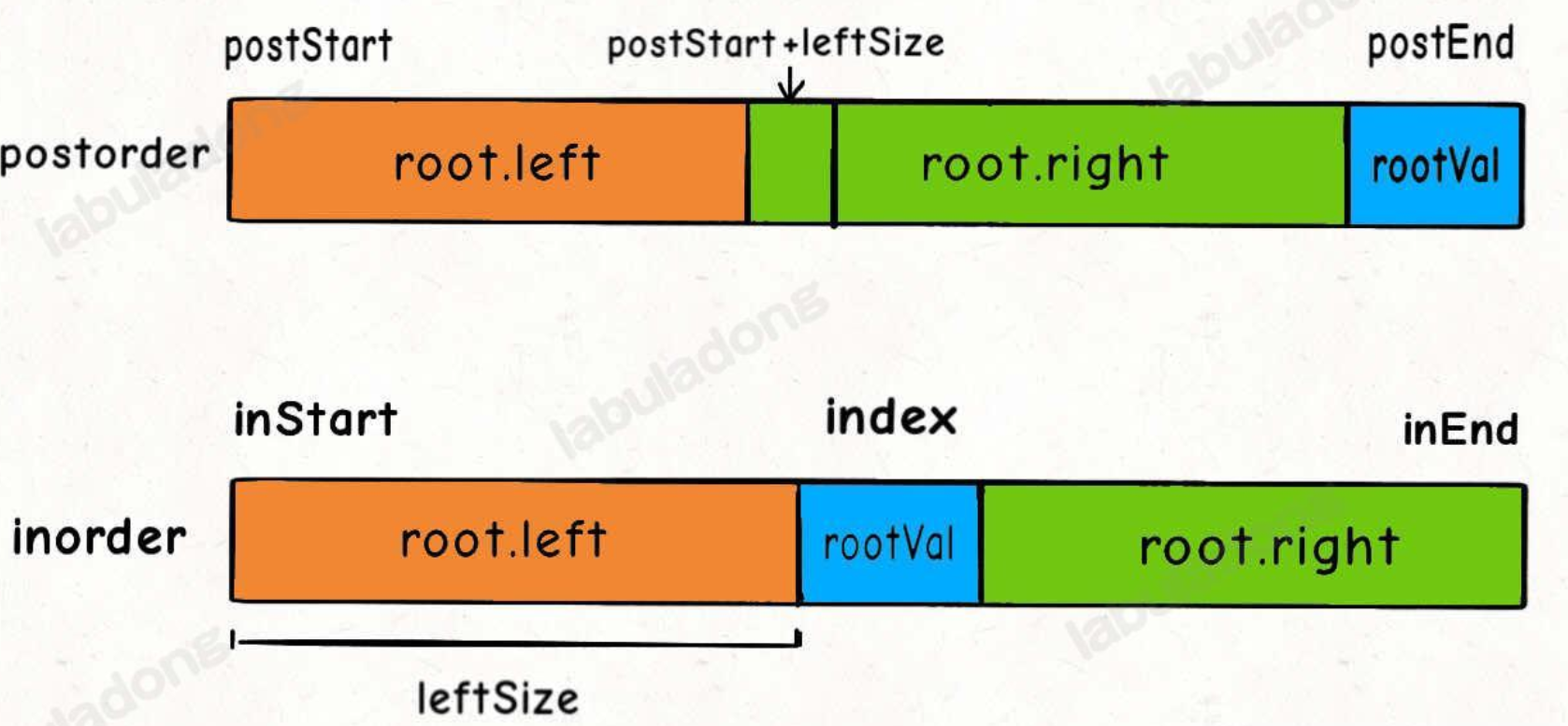
- 同上,關鍵在于四個坐標的確定要準確
-
🙇🏻?♀?代碼:
public TreeNode buildTree(int[] inorder, int[] postorder) {int inStart = 0;int inEnd = inorder.length -1;int posStart = 0;int posEnd = postorder.length - 1;return build(inorder, postorder, inStart, inEnd, posStart, posEnd);}public TreeNode build(int[] inorder, int[] postorder, int inStart, int inEnd, int posStart, int posEnd){if(posStart>posEnd){return null;}TreeNode root = new TreeNode(postorder[posEnd]);//得到根節點//找到根節點在中序數組中的位置int index = 0;int leftSize = 0;for(int i = inStart; i <= inEnd; i++ ){if(inorder[i] == root.val){index = i;leftSize = i - inStart;break;}}//*******構建左子樹右子樹 */root.left = build(inorder, postorder, inStart, index-1, posStart,posStart+leftSize -1);root.right = build(inorder, postorder, index+1, inEnd, posStart+leftSize,posEnd-1);return root;}
4、 根據前序和后序遍歷構造二叉樹
🔗889. 根據前序和后序遍歷構造二叉樹
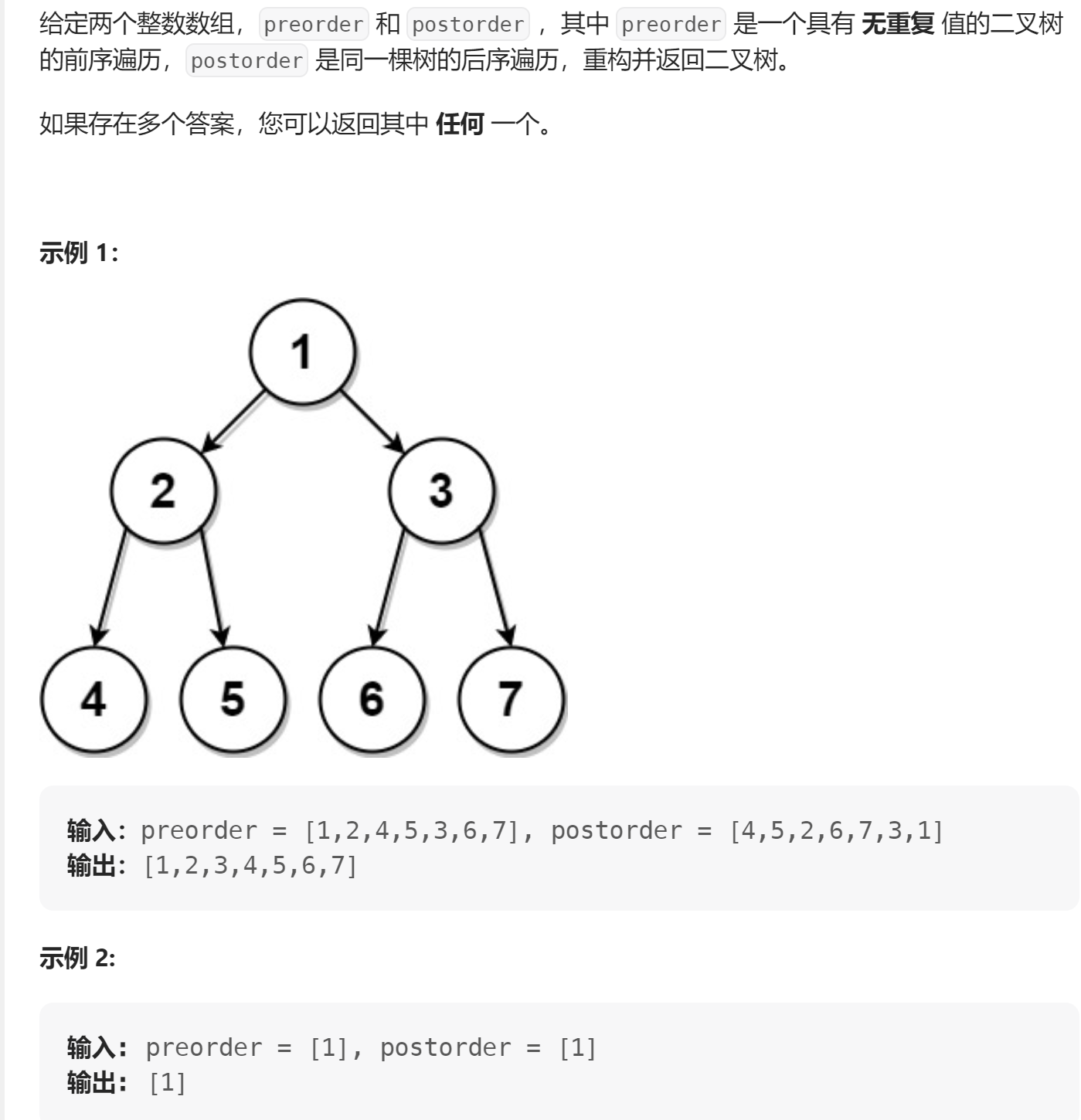
- 👧🏻思路:
-
根據我們知道,只通過前序+后序是無法唯一構造一棵二叉樹的。那么當然了,這題告訴我們有多個答案只用返回一個即可
-
前兩個(前序+中序&&中序+后序)可以唯一確定是因為通過前序/后序數組可以在前序位置唯一確定根節點root,然后在中序數組中可以根據root分成左中序數組和右中序數組,所以是可以確定唯一一顆二叉樹的。
-
而前序+后序按照這個思路其實也不是不行,因為前序和后序的數組劃分是這樣的:
🤔咦,根據上圖,貌似前序和中序可以構造唯一二叉樹呀
🙅🏻?♀?不對,因為這里我們默認了一個大前提:root+1是left子樹的跟,也就是默認了左子樹至少有一個節點。但是實際上 ,左子樹可能為空!——我們只是選取了其中一種可能情況而言。 -
🙋🏻構建思路
1. 首先將前序/后序遍歷的第一個節點作為根節點root
2. 前序數組中,root后面相鄰元素作為左子樹的根節點(坐標記為preStartL=preStart+1);
3. 根據前序數組中的左子樹根節點在后序數組中找到左子樹的根節點:坐標記為posEndL
4. 從而求得左子樹節點個數leftSize = posStartL - posStart + 1,將左右子樹劃分
5. 劃分后即可確定左右子樹的四個坐標點,帶入遞歸函數分解成子問題即可
-

-
🙇🏻?♀?代碼:
public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {int preStart = 0;int preEnd = preorder.length -1;int posStart = 0;int posEnd = postorder.length - 1;return build(preorder, postorder, preStart, preEnd, posStart, posEnd);}public TreeNode build(int[] preorder, int[] postorder, int preStart, int preEnd, int posStart, int posEnd){if (preStart > preEnd) {return null;}//****** */!注意,這種情況必須特判!*****if (preStart == preEnd) {return new TreeNode(preorder[preStart]);}//************************************* */TreeNode root = new TreeNode(preorder[preStart]);//1、得到根節點//2、key:求leftSizeint preStartL = preStart+1;//int posEndL = -1;//2.1:找左子樹根節點在后序數組中的位置for(int i = posStart; i <= posEnd; i++ ){if(postorder[i] == preorder[preStartL]){posEndL = i;break;}}int leftSize = posEndL - posStart + 1;root.left = build(preorder, postorder, preStartL, preStartL + leftSize -1, posStart, posEndL);root.right = build(preorder, postorder, preStartL + leftSize, preEnd, posEndL + 1, posEnd -1 );return root;} -
🍊注意!:在上面代碼重點標出部分,需要特判的原因是:我們在思路部分已經講過,這種方法默認左子樹至少有一個節點(一棵樹至少有兩個節點),而
preStart == preEnd并不滿足這個大前提,所以需要特判!!
💐若有不懂的地方,歡迎隨時在評論區or私信找瑤瑤子交流討論🌺

-
Java島冒險記【從小白到大佬之路】
-
LeetCode每日一題–進擊大廠
-
Go語言核心編程
-
算法






)



 Crack)








