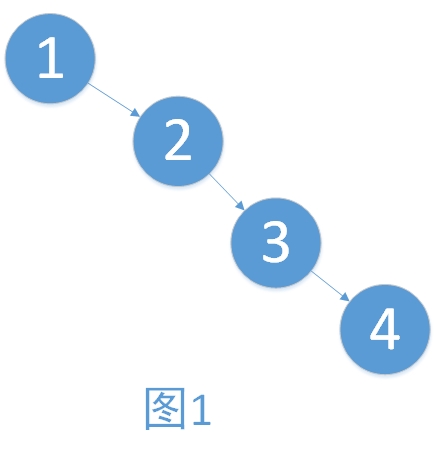
學習過了二叉查找樹,想必大家有遇到一個問題。例如,將一個數組{1,2,3,4}依次插入樹的時候,形成了圖1的情況。有建立樹與沒建立樹對于數據的增刪查改已經沒有了任何幫助,反而增添了維護的成本。而只有建立的樹如圖2,才能夠最大地體現二叉樹的優點。
? ? ? ? ? ? ? ? ? ? ? ? ??
? ? ? ? ??
在上述的例子中,圖2就是一棵平衡二叉樹。科學家們提出平衡二叉樹,就是為了讓樹的查找性能得到最大的體現(至少我是這樣理解的,歡迎批評改正)。下面進入今天的正題,平衡二叉樹。
AVL的定義
平衡二叉查找樹:簡稱平衡二叉樹。由前蘇聯的數學家Adelse-Velskil和Landis在1962年提出的高度平衡的二叉樹,根據科學家的英文名也稱為AVL樹。它具有如下幾個性質:
- 可以是空樹。
- 假如不是空樹,任何一個結點的左子樹與右子樹都是平衡二叉樹,并且高度之差的絕對值不超過1
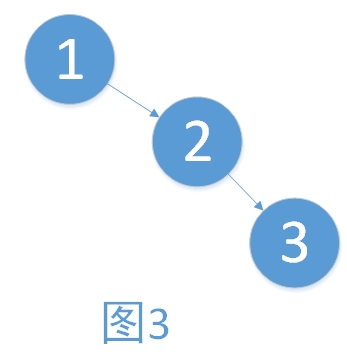
平衡之意,如天平,即兩邊的分量大約相同。如定義,假如一棵樹的左右子樹的高度之差超過1,如左子樹的樹高為2,右子樹的樹高為0,子樹樹高差的絕對值為2就打破了這個平衡。如依次插入1,2,3三個結點(如下圖)后,根結點的右子樹樹高減去左子樹樹高為2,樹就失去了平衡。
? ? ? ? ? ? ? ?
那么在建立樹的過程中,我們如何知道左右子樹的高度差呢?在這里我們采用了平衡因子進行記錄。
平衡因子:左子樹的高度減去右子樹的高度。由平衡二叉樹的定義可知,平衡因子的取值只可能為0,1,-1.分別對應著左右子樹等高,左子樹比較高,右子樹比較高。如下圖
?
說到這里,我們已經可以大概知道平衡二叉樹的結構定義需要什么內容了,數據成員,平衡因子,以及左右分支。所以,我們給出如下的結構定義。大家主要首先先了解平衡因子的各個取值及其含義即可。
typedef char KeyType;??? ?????????????? //關鍵字
typedef struct MyRcdType?? ???????? //記錄
{
??? KeyType key;
}RcdType,*RcdArr;
typedef enum MyBFStatus??????????????? //為了方便平衡因子的賦值,這里進行枚舉
{?????????????????????????? //RH,EH,LH分別表示右子樹較高,左右子樹等高,左子樹較高
??? RH,EH,LH
}BFStatus;
typedef struct MyBBSTNode??? ?? //樹結點類型定義
{
??? RcdType data;???????????????????????????? //數據成員
??? BFStatus bf;???????????????????????????????? //平衡因子
??? struct MyBBSTNode *lchild,*rchild;??????? //左右分支
}BBSTNode,*BBSTree;
AVL樹的插入時的失衡與調整
前言:這部分的失衡調整是指插入時的失衡與調整。刪除的失衡與調整與插入大致一樣,但是還是有很多不同,在后續章節講解。
一、?失衡與調整的引導
說了這么久,我們開始進入今天的重點,如何將一棵不平衡的二叉樹變成平衡二叉樹(只討論不平衡的是因為假如樹是平衡的就不必我們進行處理)。平衡二叉樹的失衡調整主要是通過旋轉最小失衡子樹來實現的。
最小失衡子樹:在新插入的結點向上查找,以第一個平衡因子的絕對值超過1的結點為根的子樹稱為最小不平衡子樹。也就是說,一棵失衡的樹,是有可能有多棵子樹同時失衡的,如下。而這個時候,我們只要調整最小的不平衡子樹,就能夠將不平衡的樹調整為平衡的樹。
在圖7中。2結點(左子樹樹高-右子樹樹高)的絕對值=2。同理,3結點的平衡因子也為2.此時同時存在了兩棵不平衡子樹,而以3為根的樹是最小的不平衡子樹。我們只要將其以3為中心,將最小不平衡樹向左旋轉,即可得到平衡二叉樹,如圖8。具體方法后續講解。
? ? ? ? ? ?
下面我們先用兩個簡單的例子來感受一下調整的方法。
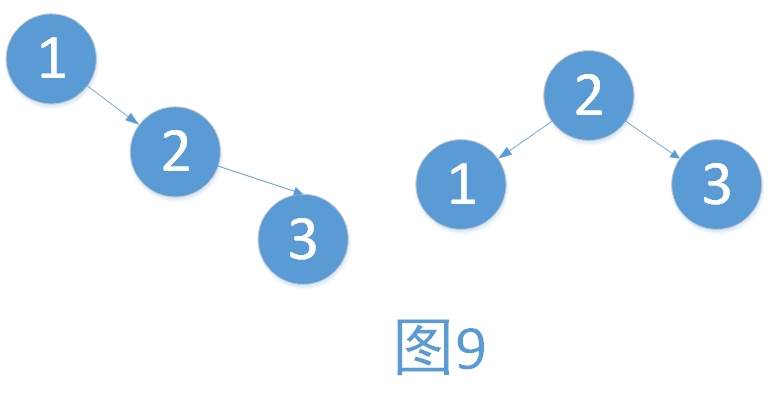
例1:右子樹過高,向左旋轉。步驟如下
? ? ? ?i. 將2作為根結點
? ? ? ii. 將1作為2的左孩子
? ? ?iii. 將2的左孩子作為1的右孩子(維護樹的有序性,只是此處為NULL而已)
? ? ? ? ? ? ??
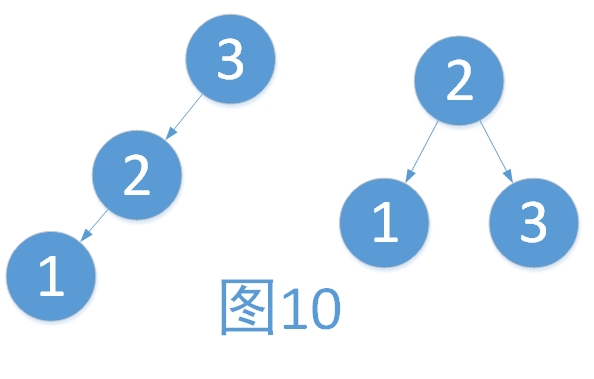
例2:左子樹過高,向右旋轉。步驟如下
? ? ? ?i. ? 將2作為根結點
? ? ? ii. ? 將3作為2的右孩子
? ? ?iii. ? 將2的右孩子作為3的左孩子(維護樹的有序性,只是此處為NULL而已)
? ? ? ? ?
下面我們再來看一個通過旋轉,但是沒辦法達到平衡的失敗例子。
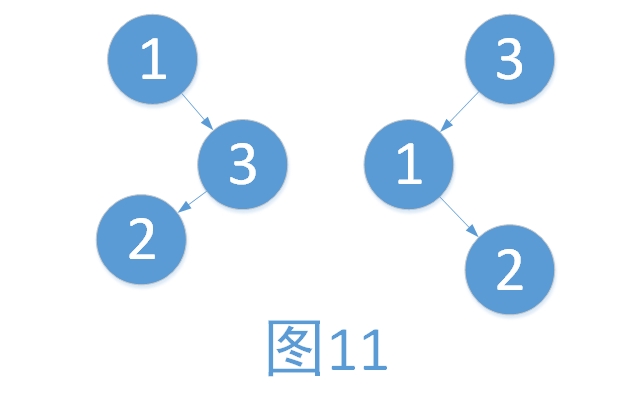
例3:右子樹過高,向左旋轉。步驟如下
? ? ? i. ? 將3作為根結點
? ? ?ii. ? 將3的左孩子作為1的右孩子
? ? iii. ? 將1作為3的左孩子
? ? ? ? ? ? ? ? ? ? ??
? ? ? ??
如上,我們發現,旋轉之后樹并沒有恢復平衡。對比圖9,我們發現,根的右子樹不一致。
在上面的三個例子我們可以看出,我們對不平衡的樹進行旋轉的時候,不僅需要考慮需要最小失衡子樹的根結點的平衡因子,還要考慮根結點較高子樹的根結點的平衡因子。如圖9與圖11中,較高子樹都為右子樹,右子樹不同,旋轉后有著完全不同的結果。
為了方便討論,我們使用連續的兩個字母來表示平衡因子,以表示各種不同的情況。第一個字母表示最小不平衡子樹根結點的平衡因子,第二個字母表示最小不平衡子樹較高子樹的根結點的平衡因子。使用L表示左子樹較高,R表示右子樹較高,E表示左右子樹等高。如上述圖11,根為的平衡因子L,較高子樹的根為L,我們將這種情況表示為LL型,再如上述例子3,根為R,較高子樹的根為L我們將這種情況稱為RL型。
下面我們將對所有的失衡情況進行討論。大致分為兩大類,一左子樹過高,二右子樹過高。順帶提一下記憶的方法,讀者對于具體某一種類型只要記住最后哪一個結點作為根即可,也就是下面標紅色的部分。
二、失衡與處理詳解
1. 左子樹過高
a) LL型
在LL型的不平衡樹中,我們首先找到最小不平衡子樹,再以其根結點向右旋轉。為何是向右旋轉呢?應該不難理解,向右旋轉后,相當于右邊的子樹樹高增加了1,而左邊的子樹樹高降低了1,而原本的樹高之差為2,那么就能夠將根的平衡因子就化為0.引用一下之前的圖如下。旋轉之后為“原來根結點的左孩子作為新的根結點”。
我們對樹以根結點為中心,向右旋轉。旋轉步驟如下
? ? i. ? 將2作為根結點
? ?ii. ? 將3作為2的右孩子
? iii. ? 將2的右孩子作為3的左孩子(維護樹的有序性,只是此處為NULL而已)
? ? ? ? ? ?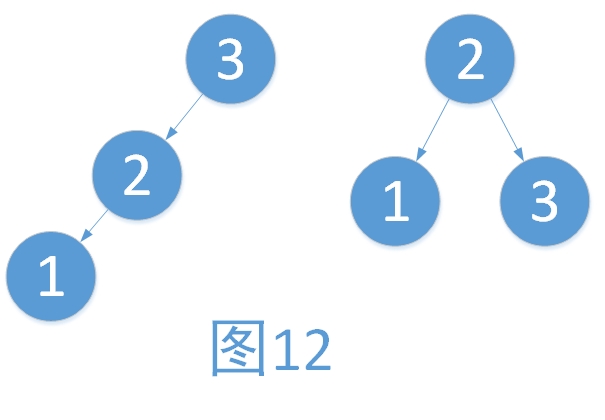
旋轉后,3與2的平衡因子為EH,1的平衡因子保持不變。
b) LE型
在這里需要說明的是,插入的時候,是不會出現LE的這種情況的。只有在刪除的時候才會出現。下面對于為何插入不可能出現做一些個人見解。
我們不妨假設存在LE的這種情況。如下。
? ? ? ? ? ??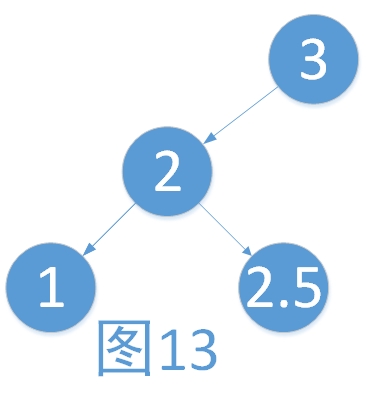
假設我們剛插入的元素是1,那么原來的樹已經不是平衡樹。不可能。
假設我們剛插入的元素是2.5,那么原來的樹也不是平衡樹,也不可能。所以說在插入的時候,是不會出現LE的這種情況的。而具體什么時候會出現呢,我們在刪除的章節進行講解。同理,不可能出現RE的情況,下面也不進行討論。讀者可以使用反證法自行驗證。
c) LR型
對于LR,要分為兩步進行旋。旋轉之后為“原來根結點的左孩子的右孩子作為新的根結點”。
第一以較高子樹的根,即1,為中心向左旋轉。具體步驟如下。
? ? ? ? ? i. 將2的左子樹作為1的右子樹(維護樹的有序性,只是此處為NULL而已)
???????? ii. ?將1作為2的左子樹
??????? iii. ?將2作為3的左子樹
? ? ? ?? ??????
??????
第二以原樹的根,即3為中心,向右旋轉。最后結果如下
?
旋轉后,1,2,3的平衡因子變為0(無需記憶)。再次發表個人意見,平衡因子要用到的時候推一下就好了。
2. 右子樹過高
a) RR型
還是引用一下之前的例子。旋轉的步驟如下。旋轉之后為“原來根結點的右孩子作為新的根結點”。
? ? ?i. ?將2作為根結點
? ? ii. ?將1作為2的左孩子
? ?iii. ?將2的左孩子作為1的右孩子(維護樹的有序性,只是此處為NULL而已)
? ? ? ??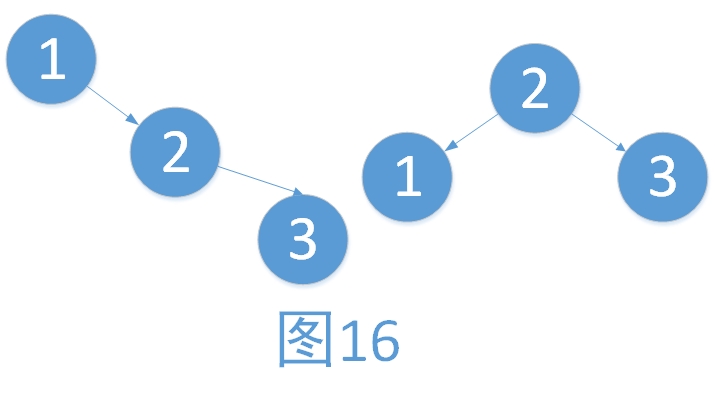
最后1,2,3的平衡因子都為EH。
b)RL型
還是引用一下之前的例子。與LR型類似,我們需要進行兩次旋轉。旋轉之后為“原來根結點的右孩子的左孩子作為新的根結點”。
第一,以根結點的右孩子即3為中心向右旋轉,結果如下。具體步驟如下
? ? ? i. ?將2作為1的右孩子
? ? ?ii. ?將3作為2的右孩子
? ? iii. ? 將2的右孩子作為3的左孩子(維護樹的有序性,只是此處為NULL而已)
? ? ? ? ? ? ??
第二,以原根結點即1,作為中心,向左旋轉。結果如下。具體步驟如下
? ? ?i. ? 將2作為根結點
? ? ii. ? 將1作為2的左孩子
? ?iii. ? 將2的左孩子作為1的右孩子(維護樹的有序性,只是此處為NULL而已)
? 
最后1,2,3的平衡因子都會EH
3、 ?插入時失衡與調整的總結
- 在所有的不平衡情況中,都是按照“尋找最小不平衡樹”->“尋找所屬的不平衡類別”->“根據4種類別進行固定化程序的操作”。
- LL,LR,RR,RL其實已經為我們提供了最后哪個結點作為新的根指明了方向。如LR型最后的根結點為原來的根的左孩子的右孩子,RL型最后的根結點為原來的根的右孩子的左孩子。我們只要記住這四種情況,可以很快地推導出所有的情況。
- 維護平衡二叉樹,最麻煩的地方在于平衡因子的維護。想要熟悉這個過程,建議讀者多多畫圖,在感官上首先體驗這個過程。
?
說到這里,我們已經了解了了解了什么是平衡二叉樹,插入結點后如何調整平衡二叉樹。我們數據結構中經常講到的有增刪查改,那么下面我們來講解一下如何刪除。
AVL樹的刪除時的失衡與調整
今天心血來潮想要寫這篇博客的原因主要就在于此。我在網上找了許久,很多人對于AVL樹的查找,插入都講解得非常精彩,但是刪除的時候卻經常貼出一段代碼,比較少有講解,對于我等需要完成作業的學生實在難受,完成作業后就希望能夠與大家分享一下。咳咳,我們回歸正題。前方高能,喝口水,看一下窗外帥哥美女再繼續看吧。
一、?????????????預備知識
1.???????樹的刪除
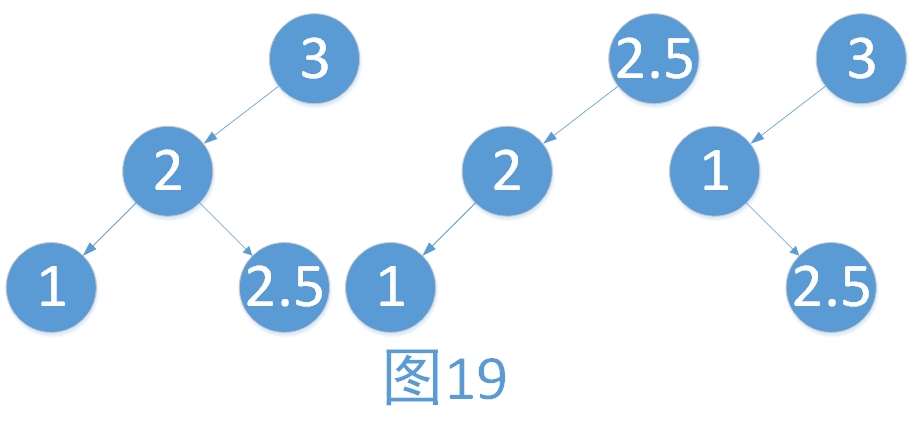
假如有一棵二叉查找樹如下,我們對它進行中序遍歷,可以得到1, 2, 2.5, 3。我們發現,這是一個遞增的序列。假如我們現在要刪除的結點為3,在不考慮樹的平衡問題時,應該哪個結點來作為頂替3的位置呢呢?答案是:對排序二叉樹進行中序遍歷時,3的直接前驅或者直接后驅。在這里,就是2.5,所以刪除后,不進行調整的結果如中間圖。假如我們現在要刪除的結點為2,在不考慮樹的平衡問題時,1頂替2的位置(假設左孩子優先于右孩子)。最后如下右圖。
具體的步驟如下:
? ? ? i. ?尋找到要刪除的結點(3)
? ? ?ii. ?將待刪除結點的直接前驅或者直接后驅賦值給待刪除結點(2.5賦值給3結點)
? ? iii. ?將直接前驅或者直接后驅刪除(將葉子結點的2.5刪除)
? 
? ? ?由于我們今天主要講的是平衡二叉樹的平衡調整,所以這部分就權當給讀者惡補一下。假如讀者還是不能理解,請先查看一下二叉查找樹的刪除,再繼續往下看。
2.???平衡因子的預告
我們已經知道,平衡因子有且僅有三種取值,LH,RH,EH。對于如下的一棵樹,刪除一個結點后
a) ? 原本樹左右子樹等高。根平衡因子的取值變化為EH->LH,EH->RH。
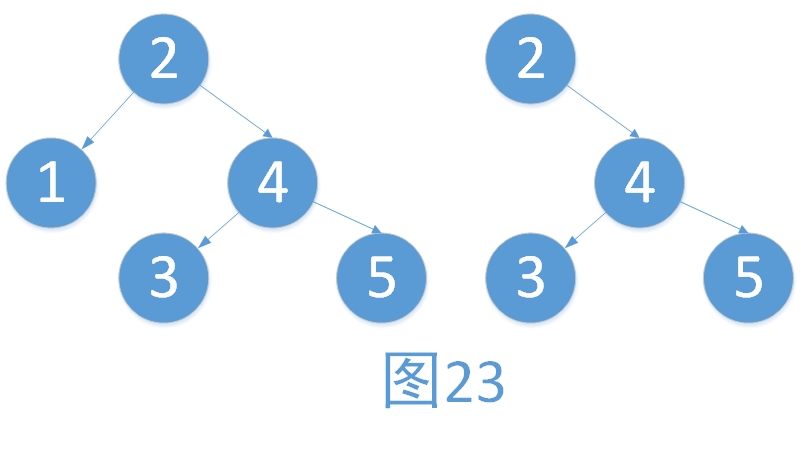
b) ? 原本樹左右子樹不等高,在較高的子樹上進行刪除,根平衡因子的取值變化為LH->EH,RH->EH。需要注意的是,當根的平衡因子變化為LH->EH,RH->EH時整棵樹的高度是下降的。最簡單的例子如下。以下兩棵樹,分別刪除1,3后,平衡因子LH->EH,RH->EH。最后樹的高度都下降了。
? 
c) ?原本樹左右子樹不等高,在較低的子樹上進行刪除,此時需要對樹進行平衡處理。如下刪除了結點1,得到右邊的不平衡樹。

? 3.???????什么會導致樹高降低
a) ? 如第2點的的第b項,根的平衡因子由LH->EH,RH->EH時整棵樹的高度是下降的。
b) ? 建立在a點以及平衡處理正確的基礎上,對樹進行正確的平衡處理后,樹高會降低。為什么呢?因為其實最小不平衡子樹進行旋轉后,最小不平衡子樹根的平衡因子總是變
為EH,或者說,平衡調整總是降低了最小不平衡子樹的高度。舉例如下。樹的高度由原來的3變為了2.

二、?????????????正式進入AVL樹的刪除與調整
1.???????刪除結點導致平衡二叉樹失衡
AVL樹也是一棵二叉查找樹,所以它的刪除也是建立在二叉查找樹的刪除之上的,只是,我們需要在不平衡的時候進行調整。而我們在預備知識的第2點中的C項中已經提及到,假如我們在較低的子樹上進行刪除,將會直接導致不平衡樹的出現。那么,我們需要進行平衡處理的,就在于此種情況。舉個栗子。
? 2.???????調整不平衡子樹后,導致了更大的不平衡子樹
假設最小不平衡子樹為A,它為雙親結點b的左子樹,而b的平衡因子為RH。假設我們現在對A進行了平衡處理,如上所講,進行平衡處理將導致樹高降低。即我們讓b較矮的子樹變得更矮了。此時對于b而言,同樣也是不平衡的。此時,我們需要再一次進行一次平衡處理。舉個栗子如下。
假設我們刪除了結點6.那么最小不平衡子樹就是1,3,5對應的二叉樹。它的雙親10的平衡因子為RH。我們首先對最小不平衡子樹進行調整,結果如右圖。我們發現,最小不平衡子樹從根結點的左子樹變成了整棵樹,所以這個時候我們又要進行一次平衡調整。具體的平衡調整步驟與插入時是一致的,在這里就贅述。
? 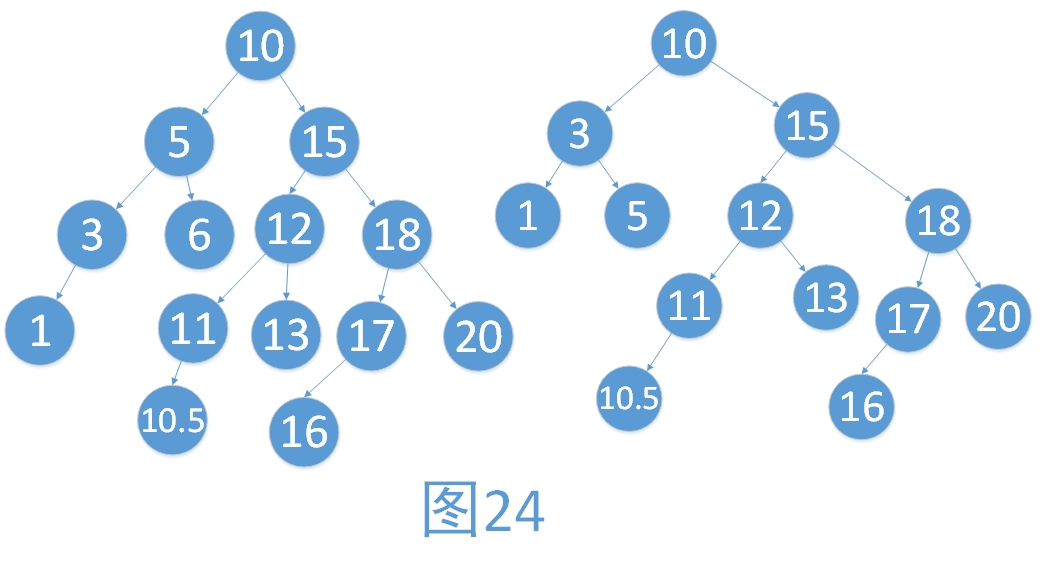
在講解插入新的結點進行平衡時,說到刪除時與插入時不有著很大的不同就在于此。插入時,進行一次平衡處理,整棵樹都會處于平衡狀態,而在刪除時,需要進行多次平衡處理,才能保證樹處于平衡狀態。
細心的朋友可能發現,上面右圖中,最小不平衡子樹的較高子樹的平衡因子為EH。這個時候,就出現了前面插入時提及的不可能出現的失衡情況。
3.???????失衡與調整的最后一種情況LE與RE
LE與RE型的失衡樹,在進行調整的時候,和LL與RR型的旋轉方式是一致的。只是最后初始根結點的平衡因子不為EH而已。就拿上面的例子而言,調整后的結果如下。初始根結點的平衡因子為RH。相對應的,假如是LE的情況,調整后初始根結點的平衡因子為LH。
?  ?
?
假如你看到了這個地方,請先為疲憊不堪的自己鼓鼓掌。本篇就到此結束,下一篇將為大家帶來具體的C代碼實現。另外,這是followDreamLgx第一次寫博客,希望大家批評改正。









)









