二分法求函數根的原理為：如果連續函數f(x)在區間[a,b]的兩個端點取值異號，即f(a)f(b)<0，則它在這個區間內至少存在1個根r，即f?=0。

二分法的步驟為：

檢查區間長度，如果小于給定閾值，則停止，輸出區間中點(a+b)/2；否則
如果f(a)f(b)<0，則計算中點的值f((a+b)/2)；
如果f((a+b)/2)正好為0，則(a+b)/2就是要求的根；否則
如果f((a+b)/2)與f(a)同號，則說明根在區間[(a+b)/2,b]，令a=(a+b)/2，重復循環；
如果f((a+b)/2)與f(b)同號，則說明根在區間[a,(a+b)/2]，令b=(a+b)/2，重復循環。
本題目要求編寫程序，計算給定3階多項式

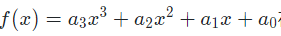
在給定區間[a,b]內的根。

輸入格式：
輸入在第1行中順序給出多項式的4個系數，在第2行中順序給出區間端點a和b。題目保證多項式在給定區間內存在唯一單根。

輸出格式：
在一行中輸出該多項式在該區間內的根，精確到小數點后2位。

輸入樣例：

3 -1 -3 1
-0.5 0.5

結尾無空行
輸出樣例：

0.33

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
double a3,a2,a1,a0;
double f(double x);
int main()
{double a,b;double mid,left,right,rst;scanf("%lf %lf %lf %lf",&a3,&a2,&a1,&a0);scanf("%lf %lf",&a,&b);left = a;right = b;while((right-left)>=0.01&&f(left)*f(right)<=0){if(!f(left)){rst = left;break;}if(!f(right)){rst = right;break;}mid = (left + right)/2;if(f(left)*f(mid)<= 0) right = mid;if(f(right)*f(mid)<= 0) left = mid;}if((right-left)<0.01)rst = (left + right)/2;printf("%.2f",rst);return 0;
}
double f(double x)
{return a3*pow(x,3)+a2*pow(x,2)+a1*x+a0;
}

第一次沒寫出來，看了別人的思路后才寫出來。
有兩點沒想到
一是沒想到用全局變量
二是沒明白精度為什么是0.01而不是我想的0.1
參考文章地址：
https://blog.csdn.net/yang8627/article/details/83038898