主要是針對字符串的匹配算法進行解說
- 有關字符串的基本知識
- 傳統的串匹配法
- 模式匹配的一種改進算法KMP算法
- 網上一比較易懂的解說
- 小樣例
- 1計算next
- 2計算nextval
- 代碼
有關字符串的基本知識
串(string或字符串)是由零個或多個字符組成的有限序列,一般記為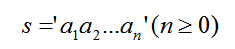
串中隨意個連續的字符組成的子序列稱為該串的子串。
包括子串的串相應的稱為主串。
通常稱字符在序列中的序號為該字符在串中的位置。子串在主串中的位置則以子串的第一個字符在主串中的位置來表示。
以下主要說一下串的模式匹配算法
傳統的串匹配法
算法的基本思想是:從主串S的第pos個字符起和模式的第一個字符比較,若相等,則繼續逐個比較興許字符;否則從主串的下一個字符起再又一次和模式的字符比較。依次類推,直至模式T中的每一個字符依次和主串S中的一個連續的字符序列相等,則匹配成功,函數值為和模式T中第一個字符相等的字符在主串S中的序號,否則稱匹配不成功。函數值為零。
此算法在最壞情況下的時間復雜度為O(m*n)
模式匹配的一種改進算法(KMP算法)
網上一比較易懂的解說
字符串匹配的KMP算法
字符串匹配是計算機的基本任務之中的一個。
舉例來說,有一個字符串”BBC ABCDAB ABCDABCDABDE”,我想知道,里面是否包括還有一個字符串”ABCDABD”?
很多算法能夠完畢這個任務,Knuth-Morris-Pratt算法(簡稱KMP)是最經常使用的之中的一個。它以三個發明者命名,起頭的那個K就是著名科學家Donald Knuth。
以下,我用自己的語言,試圖寫一篇比較好懂的KMP算法解釋。
1.
首先,字符串”BBC ABCDAB ABCDABCDABDE”的第一個字符與搜索詞”ABCDABD”的第一個字符,進行比較。由于B與A不匹配。所以搜索詞后移一位。
2.
由于B與A不匹配。搜索詞再往后移。
3.
就這樣,直到字符串有一個字符,與搜索詞的第一個字符同樣為止。
4.
接著比較字符串和搜索詞的下一個字符,還是同樣。
5.
直到字符串有一個字符,與搜索詞相應的字符不同樣為止。
6.
這時,最自然的反應是,將搜索詞整個后移一位,再從頭逐個比較。
這樣做盡管可行,可是效率非常差,由于你要把”搜索位置”移到已經比較過的位置,重比一遍。
7.
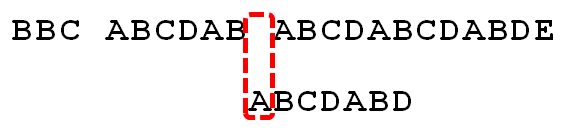
一個基本事實是,當空格與D不匹配時,你事實上知道前面六個字符是”ABCDAB”。KMP算法的想法是,設法利用這個已知信息。不要把”搜索位置”移回已經比較過的位置,繼續把它向后移,這樣就提高了效率。
8.
怎么做到這一點呢?能夠針對搜索詞,算出一張《部分匹配表》(Partial Match Table)。這張表是怎樣產生的,后面再介紹,這里僅僅要會用就能夠了。
9.
已知空格與D不匹配時,前面六個字符”ABCDAB”是匹配的。查表可知。最后一個匹配字符B相應的”部分匹配值”為2,因此依照以下的公式算出向后移動的位數:
移動位數 = 已匹配的字符數 - 相應的部分匹配值
由于 6 - 2 等于4。所以將搜索詞向后移動4位。
10.
由于空格與C不匹配,搜索詞還要繼續往后移。這時,已匹配的字符數為2(”AB”),相應的”部分匹配值”為0。所以。移動位數 = 2 - 0,結果為 2。于是將搜索詞向后移2位。
11.
由于空格與A不匹配,繼續后移一位。
12.
逐位比較,直到發現C與D不匹配。于是。移動位數 = 6 - 2,繼續將搜索詞向后移動4位。
13.
逐位比較。直到搜索詞的最后一位,發現全然匹配。于是搜索完畢。假設還要繼續搜索(即找出所有匹配)。移動位數 = 7 - 0。再將搜索詞向后移動7位。這里就不再反復了。
14.
以下介紹《部分匹配表》是怎樣產生的。
首先,要了解兩個概念:”前綴”和”后綴”。 “前綴”指除了最后一個字符以外。一個字符串的所有頭部組合;”后綴”指除了第一個字符以外。一個字符串的所有尾部組合。
15.
“部分匹配值”就是”前綴”和”后綴”的最長的共同擁有元素的長度。以”ABCDABD”為例。
- “A”的前綴和后綴都為空集。共同擁有元素的長度為0;
- “AB”的前綴為[A]。后綴為[B]。共同擁有元素的長度為0;
- “ABC”的前綴為[A, AB],后綴為[BC, C],共同擁有元素的長度0;
- “ABCD”的前綴為[A, AB, ABC],后綴為[BCD, CD, D],共同擁有元素的長度為0;
- “ABCDA”的前綴為[A, AB, ABC, ABCD],后綴為[BCDA, CDA, DA, A],共同擁有元素為”A”,長度為1;
- “ABCDAB”的前綴為[A, AB, ABC, ABCD, ABCDA]。后綴為[BCDAB, CDAB, DAB, AB, B]。共同擁有元素為”AB”,長度為2;
- “ABCDABD”的前綴為[A, AB, ABC, ABCD, ABCDA, ABCDAB],后綴為[BCDABD, CDABD, DABD, ABD, BD, D],共同擁有元素的長度為0。
16.
“部分匹配”的實質是,有時候。字符串頭部和尾部會有反復。
比方,”ABCDAB”之中有兩個”AB”,那么它的”部分匹配值”就是2(”AB”的長度)。搜索詞移動的時候,第一個”AB”向后移動4位(字符串長度-部分匹配值),就能夠來到第二個”AB”的位置。
小樣例
求字符串 ‘ababaabab’的next和nextval,結果例如以下
| j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| s[ j ] | a | b | a | b | a | a | b | a | b |
| next | 0 | 1 | 1 | 2 | 3 | 4 | 2 | 3 | 4 |
| nextval | 0 | 1 | 0 | 1 | 0 | 4 | 1 | 0 | 1 |
(1)計算next
計算next的時候須要遵循的規則例如以下
A、 j = 0 next[j] = 0
B、假設存在 Max{ k | k 屬于 (1,j-1) 且‘P1…Pk-1’= ‘Pj-k+1…Pj-1’ } (next[j] = k)
C、其它情況 next[j] = 1
| j | ( 1, k-1 ) | str(1,k-1) | ( j-k+1 , j-1 ) | str( j-k+1, j-1) | 規則 | next[ j ] |
|---|---|---|---|---|---|---|
| 2 | NULL | NULL | NULL | NULL | C | 1 |
| 3 | (1,1) | a | (2,2) | b | C | 1 |
| 4 | (1,2) | ab | (2,3) | ba | ||
| 4 | (1,1) | a | (3,3) | a | B | 2 |
| 5 | (1,3) | aba | (2,4) | bab | ||
| 5 | (1,2) | ab | (3,4) | ab | B | 3 |
| 6 | (1,4) | abab | (2,5) | baba | ||
| 6 | (1,3) | aba | (3,5) | aba | B | 4 |
| 7 | (1,5) | ababa | (2,6) | babaa | ||
| 7 | (1,4) | abab | (3,6) | abaa | ||
| 7 | (1,3) | aba | (4,6) | baa | ||
| 7 | (1,2) | ab | (5,6) | aa | ||
| 7 | (1,1) | a | (6,6) | a | B | 2 |
| 8 | (1,6) | ababaa | (2,7) | babaab | ||
| 8 | (1,5) | ababa | (3,7) | abaab | ||
| 8 | (1,4) | abab | (4,7) | baab | ||
| 8 | (1,3) | aba | (5,7) | aab | ||
| 8 | (1,2) | ab | (6,7) | ab | B | 3 |
| 9 | (1,7) | ababaab | (2,8) | babaaba | ||
| 9 | (1,6) | ababaa | (3,8) | abaaba | ||
| 9 | (1,5) | ababa | (4,8) | baaba | ||
| 9 | (1,4) | abab | (5,8) | aaba | ||
| 9 | (1,3) | aba | (6,8) | aba | B | 4 |
(2)計算nextval
nextval[i]的求解須要比較s中next[i]所在位置的字符是否與s[i]的字符一致。假設一致則用s[next[i]]的nextval的值作為nextval[i]。假設不一致,則用next[i]做為nextval[i]。
| i | next[i] | s[i] | s[ next[i] ] | yes/no | nextval[i] |
|---|---|---|---|---|---|
| 1 | 0 | a | NULL | no | next[i] = 0 |
| 2 | 1 | b | a | no | next[i] = 1 |
| 3 | 1 | a | a | yes | s[ next[i] ]的nextval = 0 |
| 4 | 2 | b | b | yes | s[2]nextval = 1 |
| 5 | 3 | a | a | yes | s[2]nextval = 0 |
| 6 | 4 | a | b | no | next[6] = 4 |
| 7 | 2 | b | b | yes | s[2] nextval = 1 |
| 8 | 3 | a | a | yes | s[3] nextval = 0 |
| 9 | 4 | b | b | yes | s[4]nextval = 1 |
代碼
該代碼參考 數據結構(C語言版) 嚴蔚敏 吳偉民 編著。。。
/*** @filename kmp.cc* @Synopsis KMP algorithm * @author XIU* @version 1* @date 2016-04-21*/
// 此代碼中所用的數組,或者是字符串都是從下標1開始#include<iostream>
#include<string.h>using namespace std;/* ============================================================================*/
/*** @Synopsis the next index data of the model string s_mode** @Param s_mode: the string* @Param next : the next array* @Param len : the length of the string*/
/* ============================================================================*/
void get_next( string s_mode, int *next, int len )
{int i = 1;int j = 0;next[1] = 0;//cout << len << endl;while( i<len ){if( j==0 || s_mode[i] == s_mode[j] ){++i;++j;if( i>len ) break;next[i] = j;if( j>len ) break;//以下的是修正的next算法(nextval)。/*if( s_mode[i] != s_mode[j]) next[i] = j;else next[i] = next[j];*/}else{j = next[j];}}for( int i=1; i<len; i++ ){cout << next[i] << " ";}cout << endl; }/* ============================================================================*/
/*** @Synopsis 利用模式串s_mode中的next函數求s_model在主串 s_primary中第pos個字符之后的位置** @Param s_primary* @Param s_mode* @Param pos* @Param next** @Returns */
/* ============================================================================*/
int Index_KMP( string s_primary, string s_mode, int pos, int *next )
{int i = pos;int j = 1;int len_p = s_primary.size();int len_m = s_mode.size();while( i < len_p && j < len_m ){if( j == 0 || s_primary[i] == s_mode[j] ){++i;++j;}elsej = next[j];}if( j >= len_m )return i - len_m;elsereturn 0;
}/* ============================================================================*/
/*** @Synopsis output function to check the result** @Param s_primary* @Param s_mode* @Param len* @Param next* @Param index*/
/* ============================================================================*/
void output( string s_primary, string s_mode, int len, int *next, int index )
{cout << "s_primary = " << s_primary << endl;cout << "s_mode = " << s_mode << endl;for( int i=1; i<len; i++ ){cout << next[i] << " ";}cout << endl; cout << "index = " << index << endl;}
int main()
{string s_primary = " acabaabaabcacaabc";string s_mode = " abaabcac";int len = s_mode.size() ;int *next = new int[len];get_next( s_mode, next, len );int tmp = Index_KMP( s_primary, s_mode, 1, next );output( s_primary, s_mode, len, next, tmp );delete [] next;return 0;
}參考網址
【1】字符串匹配的KMP算法 - 阮一峰的網絡日志
http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html
【2】KMP算法具體解釋 - joylnwang的專欄 - 博客頻道 - CSDN.NET
http://blog.csdn.net/joylnwang/article/details/6778316
【3】經典算法研究系列:六、教你初步了解KMP算法、updated - 結構之法 算法之道 - 博客頻道 - CSDN.NET
http://blog.csdn.net/v_JULY_v/article/details/6111565







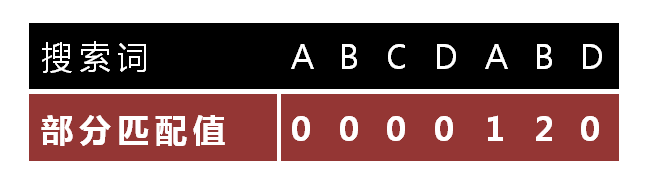





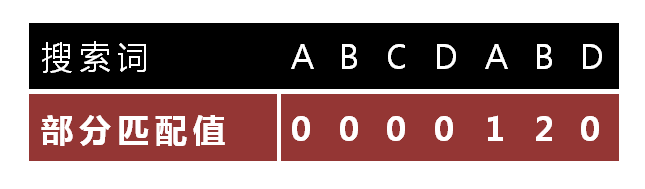


)

...)


和預防)



(IDA*))



細解幾個常用魔法方法(下))
dbca建庫)
與str.slice()區別)


