深度學習快速入門系列---損失函數

在深度學習中，損失函數的作用是量化預測值和真實值之間的差異，使得網絡模型可以朝著真實值的方向預測，損失函數通過衡量模型預測結果與真實標簽之間的差異，反映模型的性能。同時損失函數作為一個可優化的目標函數，通過最小化損失函數來優化模型參數。在本篇文章中，我們介紹一下，深度學習中最常用的幾種損失函數：

一、適用于回歸問題的損失函數

1、L1 LOSS

2、L2 LOSS

?3. smooth L1 loss

?二、適用于分類問題的損失函數

1、交叉熵損失函數

?2、Binary Cross-Entropy 交叉熵損失

3、Focal Loss

一、適用于回歸問題的損失函數

1、L1 LOSS

L1損失函數也叫作平均絕對誤差（MAE），它是一種常用的回歸損失函數，是目標值與預測值之差絕對值的和，表示了預測值的平均誤差幅度，而不需要考慮誤差的方向。總的來說，它把目標值與估計值的絕對差值的總和最小化。L1 LOSS的數學公式為：

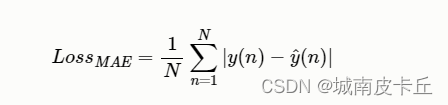
?下面演示，在pytorch中使用該函數：

import torch
import torch.nn as nnpredict=torch.randn(2,3);
target=torch.randn(2,3)print("predict:{}".format(predict))
print("target:{}".format(target))#方式一：使用Pytorch內置函數
loss1_fn=nn.L1Loss()
loss1=loss1_fn(predict,target)print("loss1:{}".format(loss1))#方式二：自己按照L1公式實現函數
loss2_fn=torch.abs(target-predict)
loss2=torch.mean(loss2_fn)print("loss2:{}".format(loss2))

從控制臺可以看到，使用pytorch內置的L1函數與我們自己實現的L1函數結果相同。

2、L2 LOSS

也被稱為均方誤差（MSE, mean squared error），它把目標值與估計值的差值的平方和最小化。其數學公式為：

?下面在pytorch中實現MSE損失函數:

import torch
import torch.nn as nn
predict=torch.rand(2,3)
target=torch.rand(2,3)
#使用pytroch內置
loss1_fn=nn.MSELoss()
loss1=loss1_fn(predict,target)
print(loss1)
#自己按照公式實現
loss2_var=predict-target
loss2_var=loss2_var**2
loss2=torch.mean(loss2_var)
print(loss2)

?3. smooth L1 loss

在提到smooth L1 loss之前，很有必要提一下L1、L2損失函數的優缺點：

L1損失函數的導數公式如下：

在這里插入圖片描述

?L2損失函數的導數公式如下：

在這里插入圖片描述

?smooth L1的公式(其中公式中的x表示，預測值與真實值的差值的絕對值)

??smooth L1的導數：

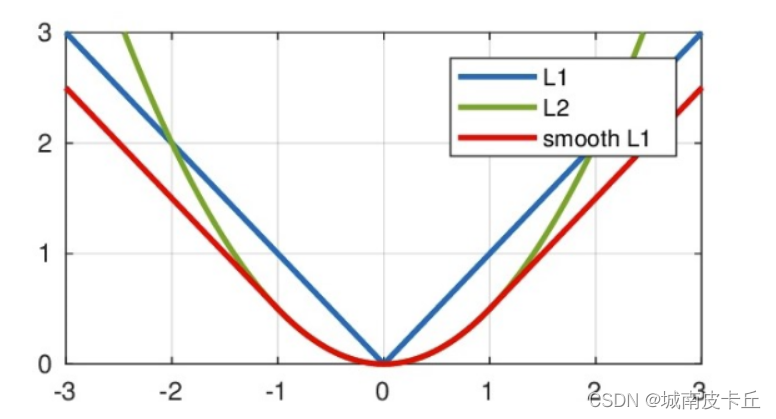
??從上圖中可以看出L1損失函數具有如下優缺點：?

優點：無論對于什么樣的輸入值，都有著穩定的梯度，不會導致梯度爆炸問題，具有較為穩健性的解
缺點：在中心點是折點，不能求導，梯度下降時要是恰好學習到w=0就沒法接著進行了

L2損失函數：?

優點：各點都連續光滑，方便求導，具有較為穩定的解
缺點：不是特別的穩健，因為當函數的輸入值距離真實值較遠的時候，對應loss值很大在兩側，則使用梯度下降法求解的時候梯度很大，可能導致梯度爆炸

盡管L1收斂速度比L2損失函數要快，并且能提供更大且穩定的梯度，但是L1有致命的缺陷：導數不連續，導致求解困難，在訓練后期損失函數將在穩定值附近波動，難以繼續收斂達到更高精度。這也導致L1損失函數極其不受歡迎。使用MAE損失（特別是對于神經網絡來說）的一個大問題就是，其梯度始終一樣:

這意味著梯度即便是對于很小的損失值來說，也還會非常大，會出現難以收斂的問題；而 MSE 當損失變小的時候，梯度也會變小，從而更容易收斂
為了修正這一點，我們可以使用動態學習率，它會隨著我們越來越接近最小值而逐漸變小。
在這種情況下，MSE會表現的很好，即便學習率固定，也會收斂。MSE損失的梯度對于更大的損失值來說非常高，當損失值趨向于0時會逐漸降低，從而讓它在模型訓練收尾時更加準確

而Smooth L1 Loss 是在 MAE 和 MSE 的基礎上進行改進得到的；在 Faster R-CNN 以及 SSD 中對邊框的回歸使用的損失函數都是Smooth L1 作為損失函數。

仔細看上面的圖像，smooth L1各點連續，在x較小時，對x的梯度也會變小，x很大時，對x的梯度的絕對值達到上限1，也不會太大導致訓練不穩定。smooth L1避開L1和L2損失的缺陷

公式以及圖像中可以看出，Smooth L1 Loss 從兩個方面限制梯度：

當預測框與 ground truth 差別過大時，梯度值不至于過大，防止梯度爆炸；
當預測框與 ground truth 差別很小時，梯度值足夠小，有利于收斂；

Smooth L1 的優點是結合了 L1 和 L2 Loss：

相比于L1損失函數，可以收斂得更快；
相比于L2損失函數，對離群點、異常值不敏感，梯度變化相對更小，訓練時不容易跑飛

下面在pytorch中實現smooth L1損失函數：

import torch
import torch.nn as nnpredict=torch.randn(2,3)
target=torch.randn(2,3)loss1_fn=nn.SmoothL1Loss()
loss1=loss1_fn(predict,target)
print(loss1)def smooth_l1_loss(x,y,beta=1):diff=torch.abs(x-y)loss2=torch.where(diff<beta,0.5*diff**2/beta,diff-0.5*beta)return loss2.mean()
loss2=smooth_l1_loss(predict,target)
print(loss2)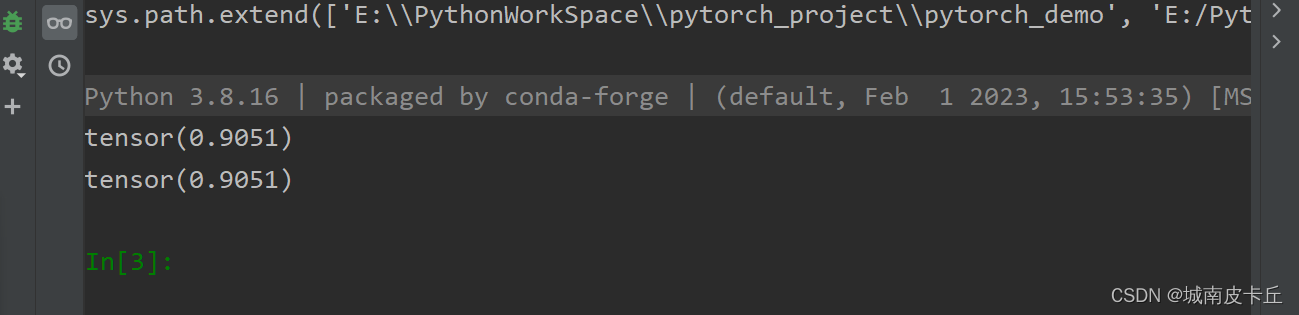

?二、適用于分類問題的損失函數

1、交叉熵損失函數

交叉熵損失函數（Cross-Entropy Loss Function）一般用于分類問題。假設樣本的標簽y ∈ {1, · · · C}為離散的類別，模型f(x, θ) ∈ [0, 1]?的輸出為類別標簽的條件概率分布，即

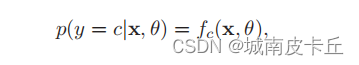
?并滿足

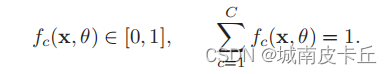
我們可以用一個C 維的one-hot向量y來表示樣本標簽。假設樣本的標簽為k，那么標簽向量y只有第k 維的值為1，其余元素的值都為0。標簽向量y可以看作是樣本標簽的真實概率分布，即第c維（記為yc，1 ≤ c ≤ C）是類別為c的真實概率。假設樣本的類別為k，那么它屬于第k 類的概率為1，其它類的概率為0。對于兩個概率分布，一般可以用交叉熵來衡量它們的差異。標簽的真實分布y和模型預測分布f(x, θ)之間的交叉熵為：

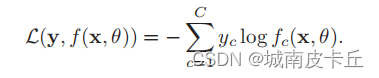
?比如對于三類分類問題，一個樣本的標簽向量為y = [0, 0, 1]T，模型預測的標簽分布為f(x, θ) = [0.3, 0.3, 0.4]T，則它們的交叉熵為：

因為 y 為 one-hot 向量，因此交叉熵損失函數公式也可以寫為：

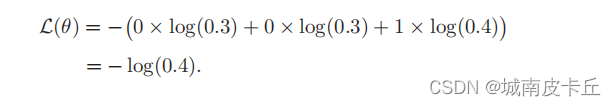
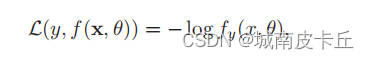
?其中fy(x, θ)可以看作真實類別y 的似然函數。因此，交叉熵損失函數也就是負對數似然損失函數（Negative Log-Likelihood Function）。

import randomimport torch
import torch.nn as nn
predict=torch.randn(2,3)
#隨機生成標簽
target=torch.tensor([random.randint(0,2) for _ in range(2)],dtype=torch.long)
# print(target)
#方式一：使用torch中定義好的函數
loss_fn=nn.CrossEntropyLoss()
loss=loss_fn(predict,target)
print(loss)
#方式二：自己按照公式實現
def cross_entropy_loss(predict,label):prob=nn.functional.softmax(predict,dim=1)log_prob=torch.log(prob)label_view=label.view(-1,1)loss=-log_prob.gather(1,label_view)loss_mean=loss.mean()return loss_mean
loss2=cross_entropy_loss(predict,target)
print(loss2)

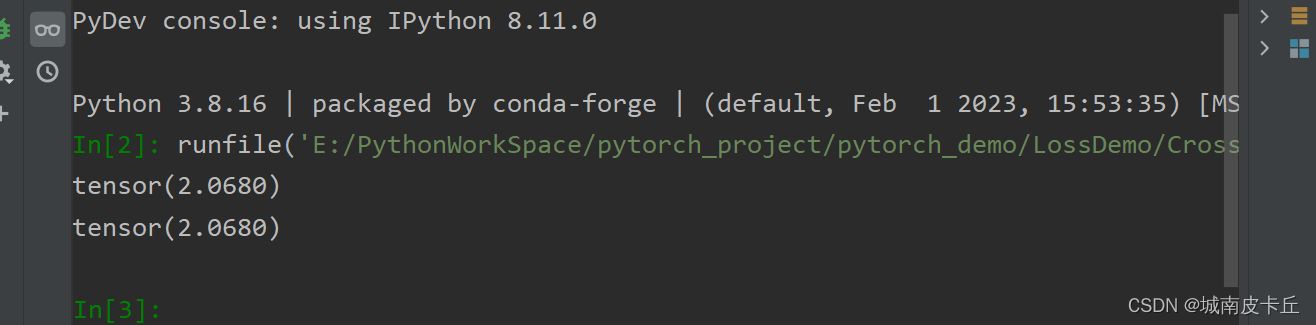
?2、Binary Cross-Entropy 交叉熵損失

Binary Cross-Entropy 交叉熵損失用于二分類問題，它其實就是交叉熵損失函數（Cross-Entropy Loss Function）的特例，也就是將多分類任務的特例化，變成二分類任務。這里不在做贅述。

3、Focal Loss

該損失函數由《Focal Loss for Dense Object Detection》論文首次提出，當時提出的背景是為了解決目標檢測領域的突出問題：

Two-stage 的目標檢測算法準確率高，但是速度比較慢；One-stage 的目標檢測算法速度雖然快很多，但是準確率比較低

想要提高 One-stage 方法的準確率，就要找到其原因，作者提出的一個原因就是正負樣本不均衡

Focal loss 損失函數是為了解決 one-stage 目標檢測中正負樣本極度不平衡的問題；
- 目標檢測算法為了定位目標會生成大量的anchor box
- 而一幅圖中目標(正樣本)個數很少，大量的anchor box處于背景區域(負樣本)，這就導致了正負樣本極不平衡
two-stage 的目標檢測算法這種正負樣本不平衡的問題并不突出，原因：
- two-stage方法在第一階段生成候選框，RPN只是對anchor box進行簡單背景和前景的區分，并不對類別進行區分
- 經過這一輪處理，過濾掉了大部分屬于背景的anchor box，較大程度降低了anchor box正負樣本的不平衡性
- 同時在第二階段采用啟發式采樣(如：正負樣本比1：3)或者OHEM進一步減輕正負樣本不平衡的問題
One-Stage 目標檢測算法，不能使用采樣操作
- Focal loss 就是專門為 one-stage 檢測算法設計的，將易區分負例的 loss 權重降低
- 使得網絡不會被大量的負例帶偏

focal loss，是在標準交叉熵損失基礎上修改得到的。這個函數可以通過減少易分類樣本的權重，使得模型在訓練時更專注于難分類的樣本。為了證明focal loss的有效性，作者設計了一個dense detector：RetinaNet，并且在訓練時采用focal loss訓練。實驗證明RetinaNet不僅可以達到one-stage detector的速度，也能有two-stage detector的準確率。在了解該損失函數的公式之前先了解一下在分類問題中常用到的交叉熵函數，交叉熵公式可以表示為：

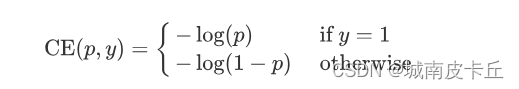
?為了方便，將交叉熵公式寫為：

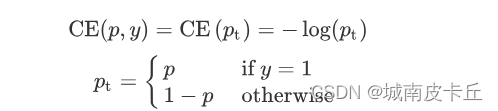
為了解決正負樣本不平衡的問題，我們通常會在交叉熵損失的前面加上一個參數? $\alpha$ ：

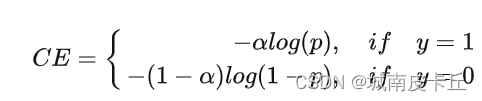
既然在 One-stage 方法中，正負樣本不均衡是存在的問題，那么一個比較常見的算法就是給正負樣本加上權重：增大正樣本的權重，減小負樣本的權重

通過設定? $\alpha$ 的值來控制正負樣本對總的 loss 的共享權重;上面的方法雖然可以控制正負樣本的權重，但是無法控制容易分類和難分類樣本的權重。因此就設計了 Focal Loss。其公式為：

?其中

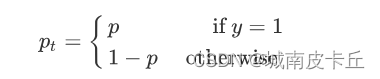
$\gamma$ 為常數，稱之為 focusing parameter ( $\gamma$ ≥ 0)，當 $\gamma$ =0?時，Focal Loss 就與一般的交叉熵損失函數一致；? $(1-p_{t})^{\gamma }$ 稱之為調制系數，目的是通過減少易分類樣本的權重，從而使得模型在訓練時更專注于難分類的樣本。當? $\gamma$ 取不同的值，Focal Loss 曲線如下圖所示，其中橫坐標是? $p_{t}$ ?縱坐標是 loss

通過 $\gamma$ 參數，解決了難易樣本分類的難題，但是我們通常還會在Focal Loss 的公式前面再加上一個參數? $\alpha$ 用于解決正負樣本不平衡的問題：

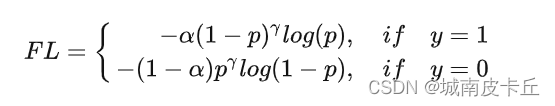
?實驗表明 $\gamma$ ?取2,? $\alpha$ 取0.25的時候效果最佳。

Focal Loss實現：

def py_sigmoid_focal_loss(pred,target,weight=None,gamma=2.0,alpha=0.25,reduction='mean',avg_factor=None):pred_sigmoid = pred.sigmoid()target = target.type_as(pred)pt = (1 - pred_sigmoid) * target + pred_sigmoid * (1 - target)focal_weight = (alpha * target + (1 - alpha) *(1 - target)) * pt.pow(gamma)loss = F.binary_cross_entropy_with_logits(pred, target, reduction='none') * focal_weightloss = weight_reduce_loss(loss, weight, reduction, avg_factor)return loss

這個代碼很容易理解，先定義一個pt：

?然后計算：

focal_weight = (alpha * target + (1 - alpha) *(1 - target)) * pt.pow(gamma)

也就是這個公式：

?然后再把BCE損失*focal_weight
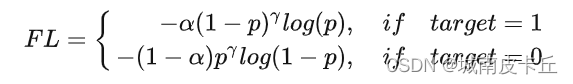