6.4圖的應用
概念回顧—生成樹
生成樹:所有頂點均由邊連接在一起,但不存在回路的圖。
- 一個圖可以有許多棵不同的生成樹、
- 含有n個頂點 n-1 條邊的圖不一定是生成樹
- 所有生成樹具有以下共同特點
- 生成樹的頂點個數與圖的頂點個數相同;
- 生成樹是圖的極小連通子圖,去掉一條邊則非連通;
- 一個有n個頂點的連通圖的生成樹有 n-1 條邊;
- 在生成樹中再加一條邊必然形成回路。
- 生成樹中任意兩個頂點間的路徑是唯一的;
6.4.1無向圖的生成樹
? 設圖G=(V,E)是個連通圖,當從圖任一頂點出發遍歷圖G時,將邊集E(G)分層兩個集合T(G)和B(G)。其中T(G)是遍歷圖時所經過的邊的集合,B(G)是遍歷圖時未經過的邊的集合。顯然,G1(V,T)是圖G的極小連通子圖。即子圖G1是連通圖G的生成樹。
6.4.2最小生成樹
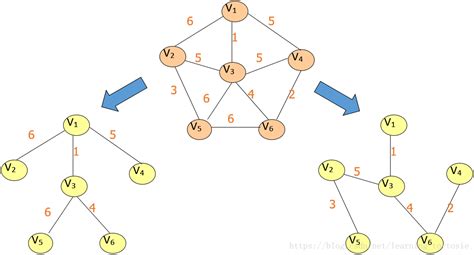
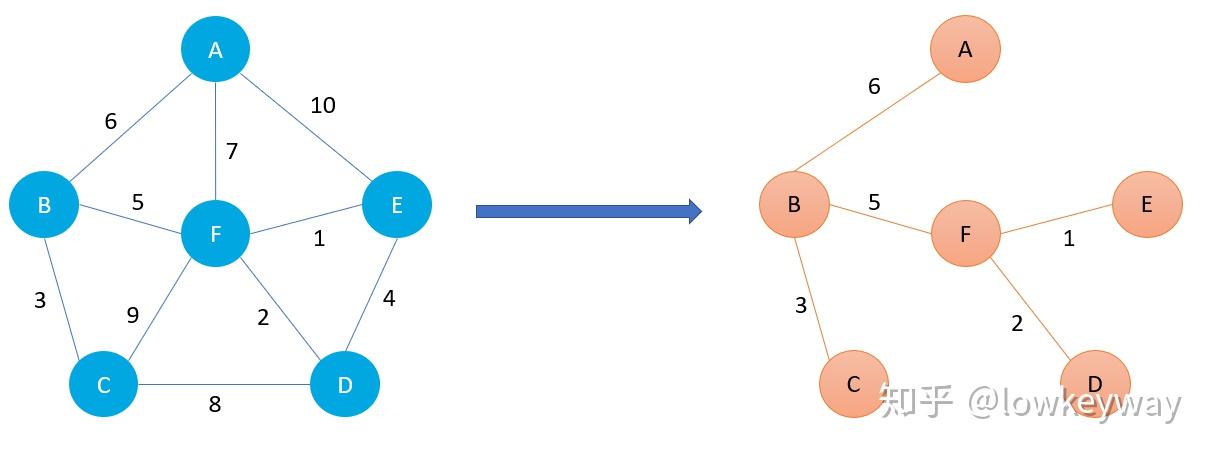
最小生成樹:給定一個無向網絡,在該網的所有生成樹中,使得各邊權值之和最小的那棵生成樹成為該網的最小生成樹,也叫最小代價生成樹。
1、構造最小生成樹
構造最小生成樹的算法很多,其中多數算法都利用了MST的性質。
MST性質:設N=(V,E)是一個連通網,U是頂點集V的一個非空子集。若邊(u,v)是一條具有最小權值的邊,其中u∈U,v∈V-U,則必存在一棵包含邊(u,v)的最小生成樹。
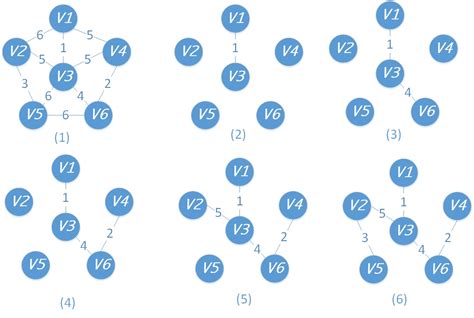
MST性質解釋:
? 在生成樹的構造過程中,圖中n個頂點分屬兩個集合:
-
已落在生成樹上的頂點集:U
-
尚未落在生成樹上的頂點集:V-U
接下來則應在所有連通U中頂點和V-U中頂點的邊中選取權值最小的邊。
2、構造最小生成樹算法
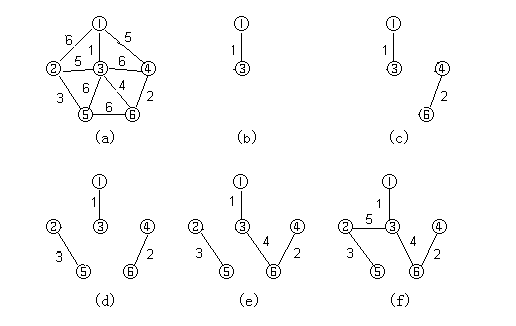
普里姆(Prim)算法
算法思想:
- 設N=(V,E)是連通網,TE是N上最小生成樹中邊的集合。
- 初始令U={u0},(u0∈V),TE={}。
- 在所有u∈U,v∈V-U的邊(u,v)∈E中,找一條代價最小的邊(u0,v0)。
- 將(u0,v0)并入集合TE,同時v0并入U。
- 重復上述操作直至U=V為止,則T=(V,TE)為N的最小生成樹。
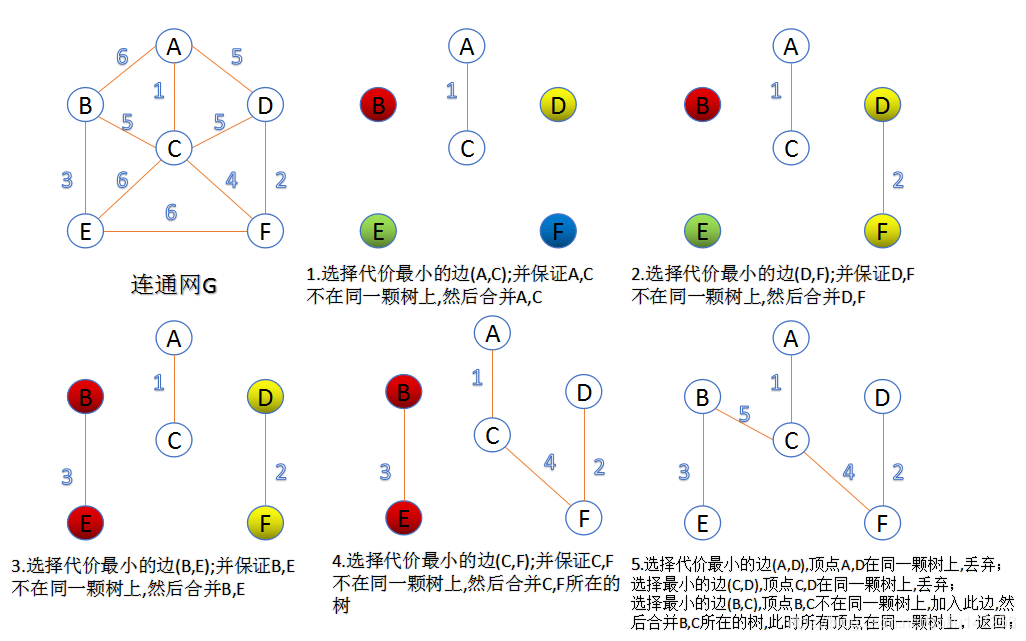
克魯斯卡爾(Kruskal)算法
算法思想:
- 設連通圖N=(V,E),令最小生成樹初始狀態只有n個頂點而無邊的非連通圖T=(V,{}),每個頂點自成一個連通分量。
- 在E中選取代價最小的邊,若該邊依附的頂點落在T中不同的連通分量上(即:不能形成環),則將此邊加入到T中;否則,舍去此邊,選取下一條代價最小的邊。
- 依此類推,直至T中所有頂點都在同一連通分量上為止。
最小生成樹可能不唯一
兩種算法比較
| 算法名 | 普里姆算法 | 克魯斯卡爾算法 |
|---|---|---|
| 算法思想 | 選擇點 | 選擇邊 |
| 時間復雜度 | O(n2) (n為頂點數) | O(eloge) (e為邊數) |
| 適應范圍 | 稠密圖 | 稀疏圖 |
6.4.3最短路徑
典型用途:交通網絡的問題—從甲地到乙地之間是否有公路連通?在有多條通路的情況下,哪一條路最短?
交通網絡用有向網來表示:
頂點——表示地點
弧——表示兩個地點有路連通,
弧上的權值——表示兩地點之間的距離,交通費或途中所花費的時間等。
? 如何能夠使一個地點到另一個地點的運輸時間最短或運費最省?這就是一個求兩個地點間的最短路徑問題。
問題抽象:在有向網中A點(源點)到達B點(終點)的多條路徑中個,尋找一條各邊權值之和最小的路徑,即最短路徑。
? 最短路徑與最小生成樹不同,路徑上不一定包含n個頂點,也不一定包含n-1條邊。
第一類問題:兩點間最短路徑
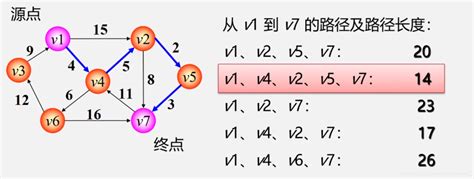
第二類問題:某源點到其他各點最短路徑

![[最短路徑問題]Dijkstra算法(含還原具體路徑) - 技術經驗 - W3xue](https://img-blog.csdnimg.cn/img_convert/ad9283be681ef22415e09b470390e446.jpeg)
兩種常見的最短路徑問題:
- 單源最短路徑—用**Dijkstra(迪杰斯特拉)**算法
- 所有頂點間的最短路徑—用**Floyd(弗洛伊德)**算法
1、Dijkstra算法
-
初始化:先找出從源點v0到各終點vk的直達路徑(v0,vk),即通過一條弧到達的路徑。
-
選擇:從這些路徑中找出一條長度最短的路徑(v0,u)
-
更新:然后對其余各條路徑進行適當的調整:
- 若在圖中存在弧(u,vk),且(v0,u)+(u,vk)<(v0,vk),則以路徑(v0,u,vk)代替(v0,vk)。
-
在調整后的各條路徑中,再找長度最短的路徑,依此類推。
迪杰斯特拉(Dijkstra)算法:按路徑長度遞增次序產生最短路徑。
-
把V分成兩組:
- S:已求出最短路徑的頂點的集合。
- T=V-S:尚未確定最短路徑的頂點集合。
-
將T中頂點按最短路徑遞增的次序加入到S中。
保證(1)從源點v0到S中各頂點的最短路徑長度都不大于從v0到T中任何頂點的最短路徑長度。
? (2)每個頂點對應一個距離值:
? S中頂點:從v0到此頂點的最短路徑長度。
? T中頂點:從v0到此頂點的只包括S中頂點作中間頂點的最短路徑長度。
所有頂點間的最短路徑:
方法一:每次以一個頂點為源點,重復執行Dijkstra算法n次。
方法二:弗洛伊德(Floyd)算法。
2、Floyd算法
算法思想:
- 逐個頂點試探
- 從vi到vj的所有可能存在的路徑中
- 選出一條長度最短的路徑
例如:采用Floyd算法,求圖中各頂點之間最短路徑
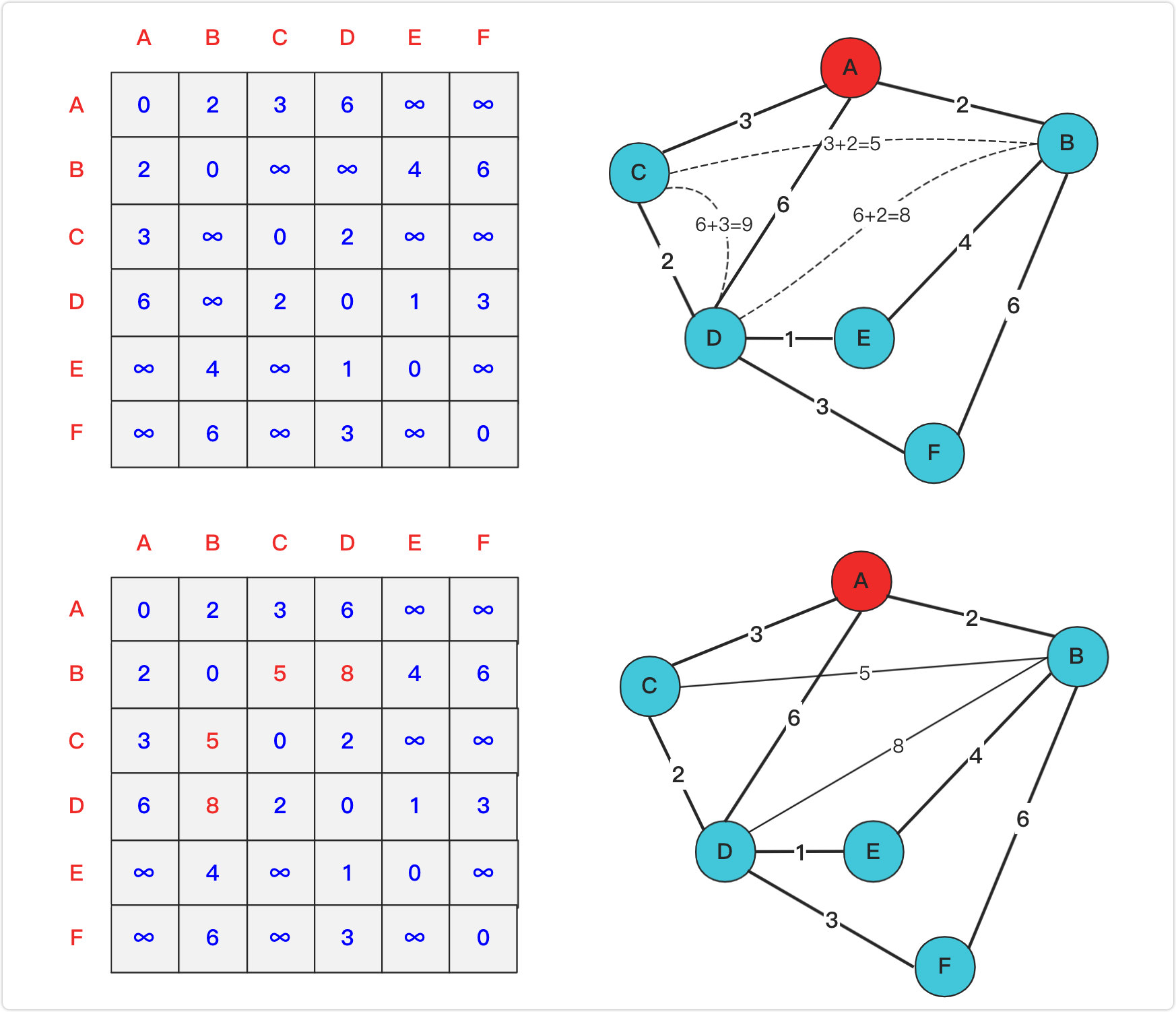
求最短路徑步驟:
? 初始時設置一個n階方陣,令其對角線元素為0,若存在弧<vi,vj>,則對應元素為權值,否則為∞
? 逐步試著在原直接路徑中增加中間頂點,若加入中間頂點后路徑變短,則修改之;否則,維持原值。所有頂點試探完畢,算法結束。
6.4.4拓撲排序
1、有向無環圖
有向無環圖:無環的有向圖,簡稱DAG圖(Directed Acycline Graph)
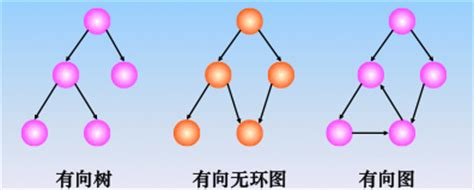
? 有向無環圖常用來描述一個工程或系統的進行過程。(通常把計劃、施工、生產、程序流程等當成是一個工程)
? 一個工程可以分為若干個子工程,只要完成了這些子工程(活動),就可以導致整個工程的完成。
**AOV網:**拓撲排序
? 用一個有向圖表示一個工程的各子工程及其相互制約的關系,其中以頂點表示活動,弧表示活動之間的優先制約關系,稱這種有向圖為頂點表示活動的網,簡稱AOV網(Activity Vertex network)。
? 特點:
- 若從 i 到 j 有一條有向路徑,則 i 是 j 的前驅;j 是 i 的后繼。
- 若<i,j>是網中有向邊,則 i 是 j 的直接前驅;j 是 i 的直接后繼。
- AOV網中不允許有回路,因為如果有回路存在,則表明某項活動以自己為先決條件,顯然這是荒謬的。
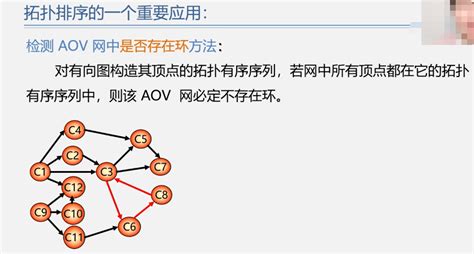
問題:如何判別AOV網中是否存在回路?
**AOE網:**關鍵路徑
? 用一個有向圖表示一個工程的各子工程及其相互制約的關系,以弧表示活動,以頂點表示活動的開始或結束事件,稱這種有向圖為邊表示活動的網,簡稱為AOE網(Activity On Edge)。
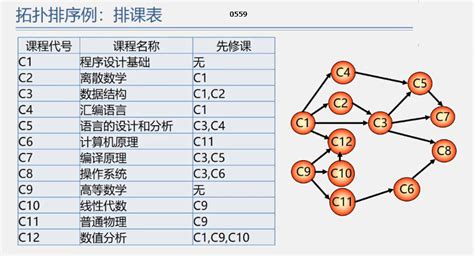
拓撲排序
? 在AOV網沒有回路的前提下,我們將全部活動排列成一個線性序列,使得若AOV網中有弧<i,j>存在,則在這個序列中,i 一定排在 j 的前面,具有這個性質的線性序列稱為拓撲有序序列,相應的拓撲有序排序的算法稱為拓撲排序。
拓撲排序的方法:
- 在有向圖中選一個沒有前驅的頂點且輸出之。
- 從圖中刪除該頂點和所有以它為尾的弧。
- 重復上述兩步,直至全部頂點均已輸出;或者當圖中不存在無前驅的頂點為止。

一個AOV網的拓撲序列不是唯一的
檢測AOV網中是否存在環方法:
? 對有向圖構造其頂點的拓撲有序序列,若網中所有頂點都在它的拓撲有序序列中,則該AOV網必定不存在環。
關鍵路徑
? 把工程計劃表示為邊表示活動的網絡,即AOE網,用頂點表示事件,弧表示活動,弧的權表示活動持續時間。
事件表示在它之前的活動已經完成,在它之后的活動可以開始。
對于AOE網,我們關心兩個問題:
- 完成整項工程至少需要多少時間?
- 那些活動是影響工程進度的關鍵?
關鍵路徑——路徑長度最長的路徑。
路徑長度——路徑上各活動持續時間之和。
如何確定關鍵路徑,需要定義4個描述量:
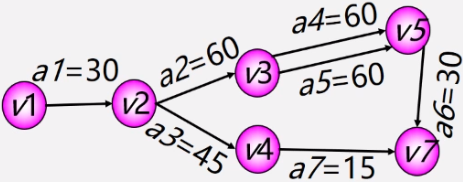
ve(vj)——表示事件 vj 的最早發生時間。
? 例如:ve(v1)=0 ve(v2)=30
vl(vj)——表示事件 vj 的最遲發生時間。
? 例如:vl(v4)=165
e(i)——表示活動 ai 的最早開始時間。
? 例如:e(a3)=30
l(i)——表示活動 ai 的最遲開始時間。
? 例如:l(a3)=120
l(i) - e(i)——表示完成活動 ai 的時間余量。
? 例如:l(3) - e(3)=90
關鍵活動——關鍵路徑上的活動,即 l(i)==e(i)(即l(i) - e(i) == 0)的活動。

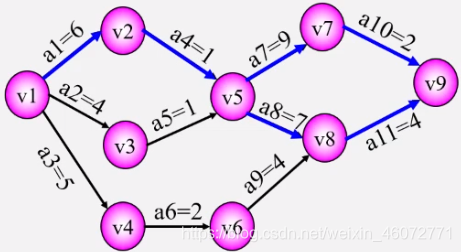
關鍵路徑的討論
-
若網中有幾條關鍵路徑,則需加快同時在幾條關鍵路徑上的關鍵活動。
如:a11,a10,a8,a7。
-
如果一個活動處于所有的關鍵路徑上,那么提高這個活動的速度,就能縮短整個工程的完成時間。如:a1、a4。
-
處于所有的關鍵路徑上的活動完成時間不能縮短太多,否則會使原來的關鍵路徑變成不是關鍵路徑。這時,必須重新尋找關鍵路徑。如:a1由6天變成3天,就會改變關鍵路徑。


創新研究團隊前往靈境至維·既明科技進行拜訪交流)



——堆棧窗口 QStackedWidget)










+測試數據集)
,計算機視覺(CV),語音識別,多模態等任務)

