1、位移不變性

它指的是無論物體在圖像中的什么位置，卷積神經網絡的識別結果都應該是一樣的。

因為CNN就是利用一個kernel在整張圖像上不斷步進來完成卷積操作的，而且在這個過程中kernel的參數是共享的。換句話說，它其實就是拿了同一張“通緝令”在“全國范圍”內查找“嫌疑犯”，這樣一來理論上就具備了位移不變性了(當然，受限于步進跨度、卷積核大小等因素的影響，某些條件下CNN也可能會存在“漏”的情況)。

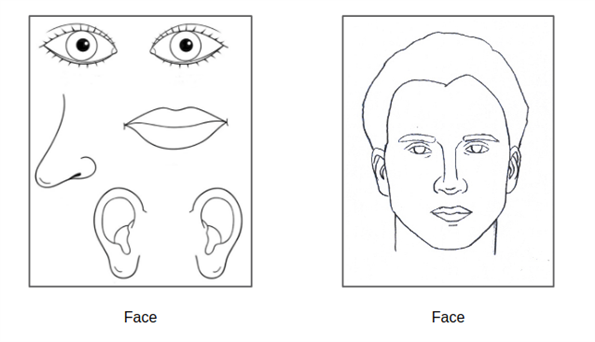
圖???CNN缺乏“空間整體”理解

CNN會將上述兩個圖都判定為face——這是因為組成face的各個部件確實都在圖像中出現了，只不過它們的排列是混亂的。但對于人類來說，這樣的預測結果顯然是比較“滑稽可笑”的，或者說無法接受的。

?Capsule Network據說可以給出有效的解決辦法

2、? 尺寸不變性

尺度不變性，簡單來講就是指物體在被測試圖像中的尺寸大小原則上不會影響模型的預測結果。

卷積神經網絡，它的kernel size做為超參數是固定大小的，并不會動態調節。

通過小尺寸filter的堆疊來達到同樣的效果，實際上比直接用大尺寸filter更節省參數數量，所以可以看到現在各個主流的神經網絡框架中用的filter size普遍都不大(或者小尺寸filter占比高)。當然，這也并不代表大尺寸的filter“一無事處”。如果某些情況下大尺寸的filter剛好可以匹配到特征，那么此時它的效率要高于小尺寸的堆疊。正是基于這樣的考慮，有些神經網絡框架會選擇“大小通吃”的策略來選擇卷積核，比如著名的inception model。

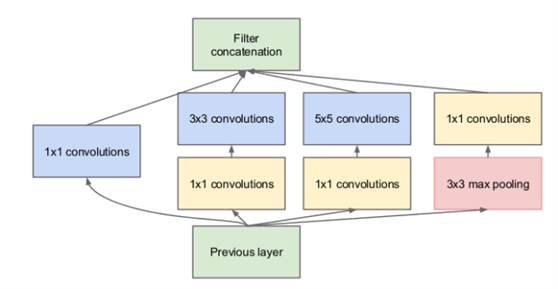
所以簡單來說，卷積神經網絡就是通過“大”和“小”卷積核的搭配和層疊，來滿足圖像識別中的尺度不變性的要求，同時降低參數數量的。?

3、? 旋轉不變性

旋轉不變性，簡單來講是指物體的旋轉角度不會影響模型的預測結果。

(1)?池化層的“順帶”作用

我們知道，max pooling是針對數據在一定范圍內取它們的最大值，比如下面所示的是2*2空間大小的操作范例：

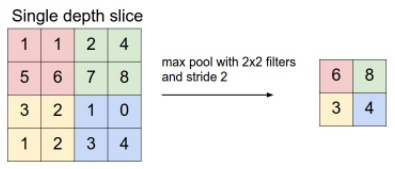
這種操作過程“順帶”賦予了CNN一個關鍵能力——即物體在旋轉一定的小角度后，有某些概率下得到的結果值不會產生變化，從而讓它似乎“具備”了旋轉不變性。

從上述的描述中我們也可以看到，CNN的這種旋轉不變性其實是“不可靠”的，帶有一定的隨機性質。

(2)?數據增強起到了作用

正因為算法層面對于旋轉不變性沒有特殊的設計，所以我們在應用卷積神經網絡時更要重視這一問題。一種典型的辦法就是采用數據增強，以“人為構造數據的方式”提升訓練出來的模型在應對“旋轉”問題時的魯棒性。

數據增強在深度神經網絡中的重要性是毋庸置疑的。