概率圖模型（Probabilistic Graphical Model，PGM），是一種用圖結構來描述多元隨機變量之間條件獨立性的概率模型。它可以用來表示復雜的概率分布，進行有效的推理和學習，以及解決各種實際問題，如圖像處理，自然語言處理，生物信息學，社會網絡分析等。

概率圖模型有兩大類：有向圖模型和無向圖模型。有向圖模型使用有向非循環圖（Directed Acyclic Graph，DAG）來表示變量之間的因果關系，也稱為貝葉斯網絡（Bayesian Network）或信念網絡（Belief Network）。無向圖模型使用無向圖（Undirected Graph）來表示變量之間的相關關系，也稱為馬爾可夫網絡（Markov Network）或馬爾可夫隨機場（Markov Random Field）。

概率圖模型的基本問題有三個：表示、推斷和學習。表示問題是指如何用圖結構和參數來定義一個概率分布。推斷問題是指如何根據已知的觀測變量和參數，計算未知的隱變量或者邊緣概率。學習問題是指如何根據已知的觀測數據，估計未知的參數或者圖結構。

為了讓你更清楚地理解概率圖模型的含義，我為你準備了以下的例子：

假設你有一個朋友圈，其中有五個人：Alice, Bob, Carol, David和Eve。你想要知道他們之間的友誼關系，以及他們的喜好和性格。你可以用一個概率圖模型來表示這個問題，如下圖所示：

?

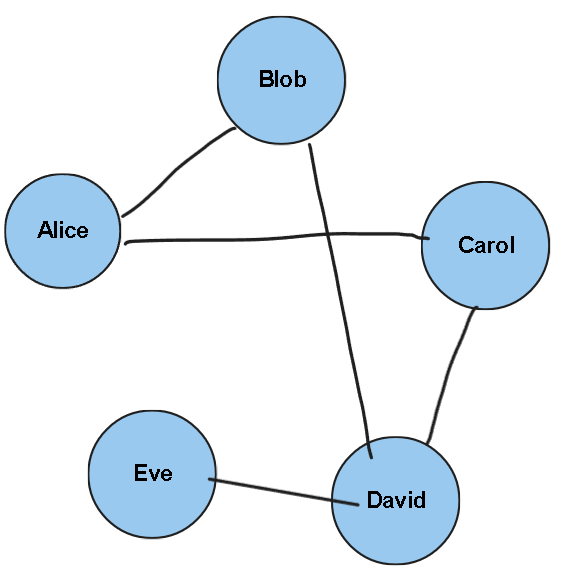?這個圖中，每個節點代表一個人，每個節點有兩個屬性：愛好（hobby）和性格（personality）。每條邊代表兩個人之間是否是朋友。這個圖就是一個無向圖模型的例子，它可以用來表示五個人的愛好和性格的聯合概率分布，以及他們之間的友誼關系。

?

這個公式的含義是：五個人的愛好和性格的聯合概率分布等于所有可能的組合乘以相應的勢函數再除以歸一化常數。勢函數可以看作是一種度量變量之間相關程度的函數，它越大，說明變量之間越相關；它越小，說明變量之間越獨立。?