• 博主簡介：努力學習的22級計算機科學與技術本科生一枚🌸
• 博主主頁： @是瑤瑤子啦
• 每日一言🌼: 所謂自由，不是隨心所欲，而是自我主宰。——康德

一、二叉樹刷題綱領

• 🍊 二叉樹解題的思維模式分兩類：

  • 1、是否可以通過遍歷一遍二叉樹得到答案？如果可以，用一個 traverse 函數配合外部變量來實現，這叫「遍歷」的思維模式。(對應：回溯算法）

  void traverse(TreeNode root) {if (root == null) {return;}// 前序位置traverse(root.left);// 中序位置traverse(root.right);// 后序位置
  }

  • 2、是否可以定義一個遞歸函數，通過子問題（子樹）的答案推導出原問題的答案？如果可以，寫出這個遞歸函數的定義，并充分利用這個函數的返回值，這叫「分解問題」的思維模式。（對應：動態規劃算法）

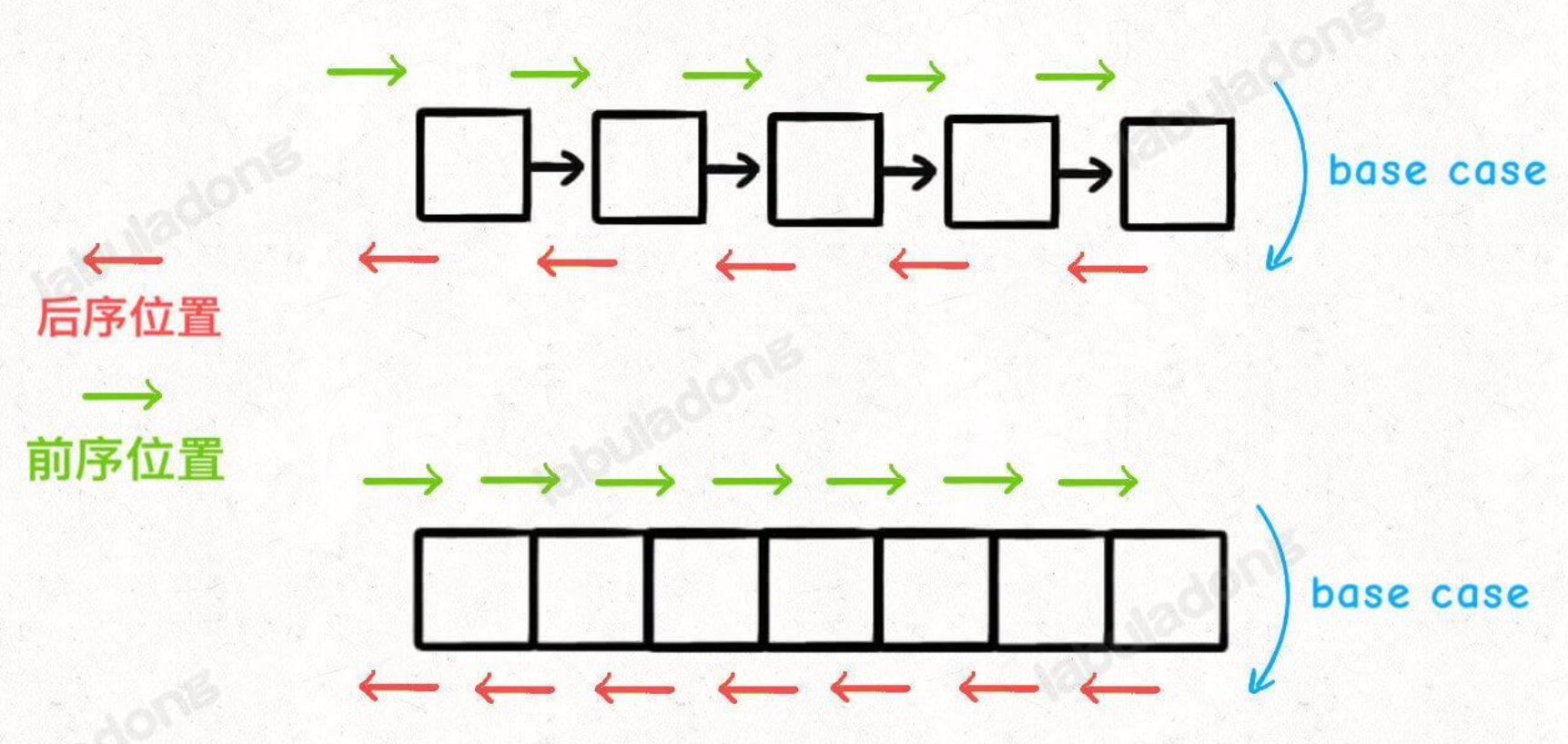
• 🍊 前中后序

  • 所謂前序位置，就是剛進入一個節點（元素）的時候，后序位置就是即將離開一個節點（元素）的時候，那么進一步，你把代碼寫在不同位置，代碼執行的時機也不同
  • 前序位置的代碼只能從函數參數中獲取父節點傳遞來的數據，而后序位置的代碼不僅可以獲取參數數據，還可以獲取到子樹通過函數返回值傳遞回來的數據。
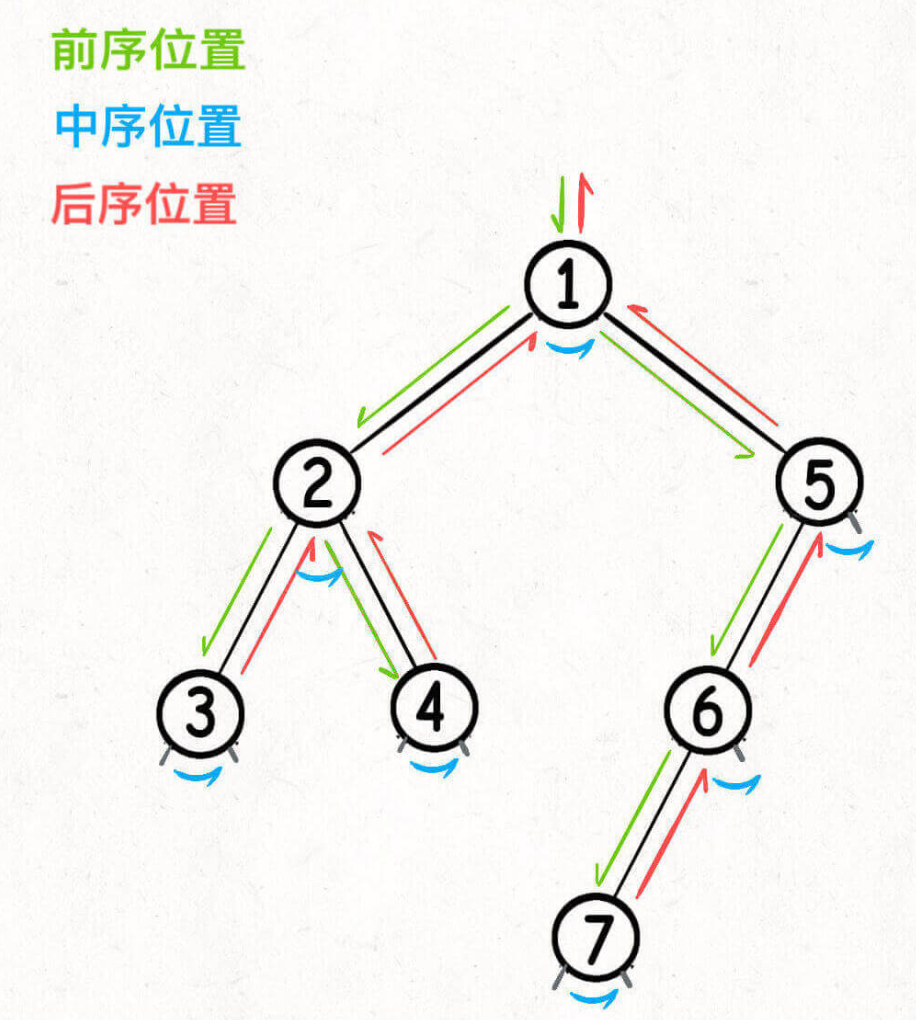
  • 🌟二叉樹的所有問題，就是讓你在前中后序位置注入巧妙的代碼邏輯，去達到自己的目的，你只需要單獨思考每一個節點應該做什么，其他的不用你管，拋給二叉樹遍歷框架，遞歸會在所有節點上做相同的操作。

  
  

• 🍊一道二叉樹的題目時的通用思考過程

  1. 是否可以通過遍歷一遍二叉樹得到答案？如果可以，用一個 traverse 函數配合外部變量來實現。

  2. 是否可以定義一個遞歸函數，通過子問題（子樹）的答案推導出原問題的答案？如果可以，寫出這個遞歸函數的定義，并充分利用這個函數的返回值。

  3. 無論使用哪一種思維模式，你都要明白二叉樹的每一個節點需要做什么，需要在什么時候（前中后序）做。

二、刷題

1、104. 二叉樹的最大深度

🔗104. 二叉樹的最大深度

• 👧🏻思路：分解成子問題，maxDepth = 1 + 左子樹最大高度+右子樹最大高度

• 🙇🏻?♀?代碼：

   public int maxDepth(TreeNode root) {//臨界條件if(root == null){return 0;}int leftHeight = maxDepth(root.left);//求左子樹最大高度int rightHeight = maxDepth(root.right);//求右子樹最大高度return 1 + Math.max(leftHeight, rightHeight);}
  

2、 二叉樹的前序遍歷（非遞歸）

🔗144. 二叉樹的前序遍歷

• 👧🏻思路：分解成子問題，遞歸序列 = add(自身節點）+ add(左子樹的遞歸序列） + add(右子樹的遞歸序列）

• 🙇🏻?♀?代碼：

   public List<Integer> preorderTraversal(TreeNode root) {List<Integer> ret = new LinkedList<>();if(root == null){return ret;}ret.add(root.val);if(root.left!=null){List<Integer> leftList = preorderTraversal(root.left);ret.addAll(leftList);}if(root.right!=null){List<Integer> rightList = preorderTraversal(root.right);ret.addAll(rightList);}return ret;}
  

3、 二叉樹的直徑

🔗543. 二叉樹的直徑

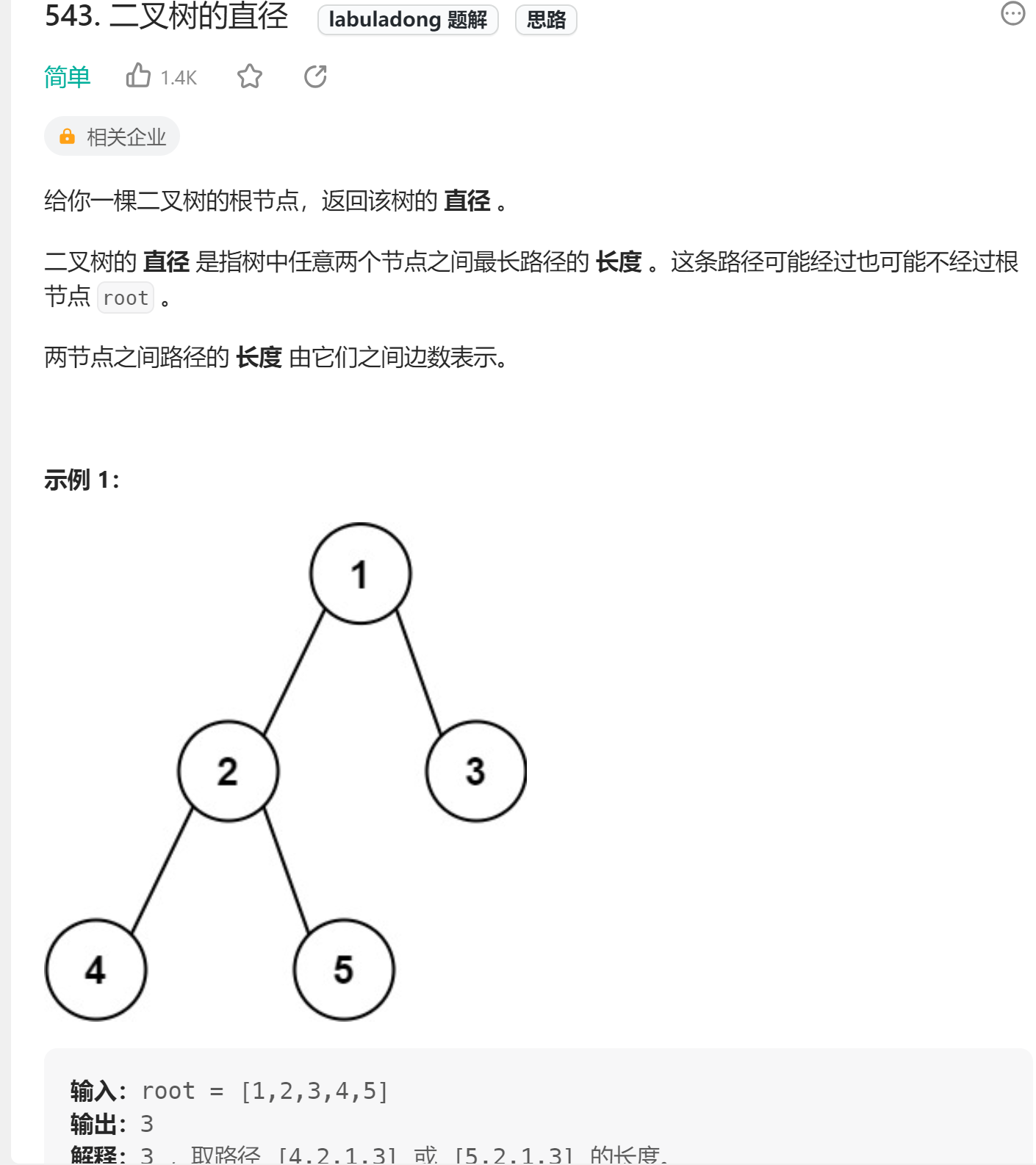
• 👧🏻思路：兩種模式的結合，首先大的背景是利用maxDepth進行二叉樹的后序遍歷+求當前節點左右子樹的最大高度.注意需要一個外部變量maxDiameter來時刻更新最大直徑。（這種思路是O(n)的時間復雜度，可以用遍歷每個節點+求當前節點的最大直徑，思路是一樣的，但是復雜度度是O(n2)，因為在本方法中在求maxDepth的時候就已經順帶遍歷了整個節點！）
  

• 🙇🏻?♀?代碼：

  	public int maxDiameter;public int diameterOfBinaryTree(TreeNode root) {maxDepth(root);return maxDiameter;}public int maxDepth(TreeNode root) {if(root == null){return 0;}//計算當前節點的左子樹最大高度int leftH = maxDepth(root.left);//計算當前節點的右子樹的最大高度int rightH = maxDepth(root.right);maxDiameter = Math.max(maxDiameter,leftH + rightH);//更新maxDiameterreturn 1 + Math.max(leftH, rightH);}
  

---

💐若有不懂的地方，歡迎隨時在評論區or私信找瑤瑤子交流討論🌺

• Java島冒險記【從小白到大佬之路】
  

• LeetCode每日一題–進擊大廠

• Go語言核心編程
  

• 算法