一、樹的概念及結構
1、樹的概念
樹 是一種非線性的數據結構,它是由n(n>=0)個有限結點組成一個具有層次關系的集合。把它叫做樹是因 為它看起來像一棵倒掛的樹,也就是說它是根朝上,而葉朝下的。
- 有一個特殊的結點,稱為根結點,根節點沒有前驅結點。
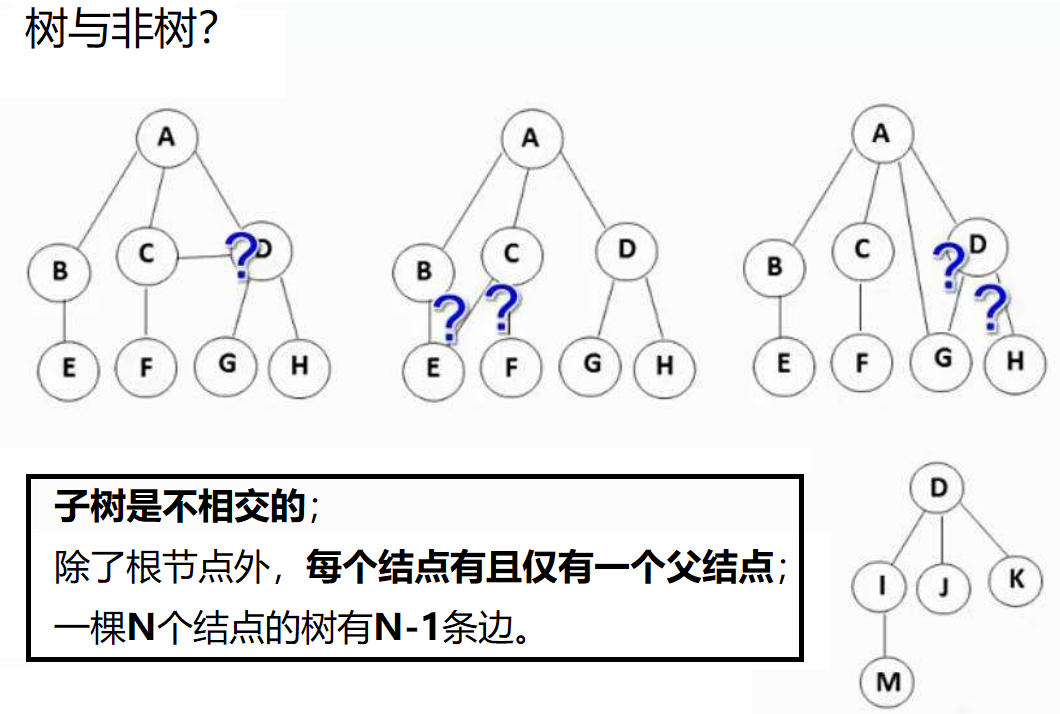
- 除根節點外,其余結點被分成M(M>0)個互不相交的集合T1、T2、……、Tm,其中每一個集合 Ti (1<= i <= m) 又是一棵結構與樹類似的子樹。每棵子樹的根結點有且只有一個前驅,可以有0個或多個后繼。
- 因此,樹是遞歸定義的。
現實生活中的樹:???????????????????????????????????????????????????????數據結構中的樹:


注意:樹形結構中,子樹之間不能有交集,否則就不是樹形結構。
2、樹的相關概念
- 節點的度:一個節點含有的子樹的個數稱為該節點的度; 如上圖:A 的度為 6。
- 葉節點或終端節點:度為 0 的節點稱為葉節點; 如上圖:B、C、H、I...等節點為葉節點。
- 非終端節點或分支節點:度不為 0 的節點; 如上圖:D、E、F、G...等節點為分支節點。
- 雙親節點或父節點:若一個節點含有子節點,則這個節點稱為其子節點的父節點; 如上圖:A 是 B 的父節點。
- 孩子節點或子節點:一個節點含有的子樹的根節點稱為該節點的子節點; 如上圖:B是A的孩子節點。
- 兄弟節點:具有相同父節點的節點互稱為兄弟節點; 如上圖:B、C 是兄弟節點。
- 樹的度:一棵樹中,最大的節點的度稱為樹的度; 如上圖:樹的度為 6。
- 節點的層次:從根開始定義起,根為第1層,根的子節點為第 2 層,以此類推。
- 樹的高度或深度:樹中節點的最大層次; 如上圖:樹的高度為 4。
- 堂兄弟節點:雙親在同一層的節點互為堂兄弟;如上圖:H、I互為兄弟節點。
- 節點的祖先:從根到該節點所經分支上的所有節點;如上圖:A 是所有節點的祖先。
- 子孫:以某節點為根的子樹中任一節點都稱為該節點的子孫。如上圖:所有節點都是 A 的子孫。
- 森林:由m(m>0)棵互不相交的樹的集合稱為森林。
3、樹的表示
樹結構相對線性表比較復雜,要存儲表示起來就比較麻煩。既然保存值域,也要保存結點和結點之間 的關系,實際中樹有很多種表示方式如:雙親表示法,孩子表示法、孩子雙親表示法以及孩子兄弟表示法等。我們這里就簡單的了解其中最常用的孩子兄弟表示法。
// 孩子兄弟表示法
typedef int DataType;
struct Node
{struct Node* firstChild1; // 第一個孩子結點struct Node* pNextBrother; // 指向其下一個兄弟結點DataType data; // 結點中的數據域
};4、樹在實際中的運用(表示文件系統的目錄樹結構)

二、二叉樹的概念及結構
1、概念
一棵二叉樹是結點的一個有限集合,該集合:
- 或者為空
- 由一個根節點加上兩棵別稱為左子樹和右子樹的二叉樹組成

從上圖可以看出:
- 二叉樹不存在度大于 2 的結點。
- 二叉樹的子樹有左右之分,次序不能顛倒,因此二叉樹是有序樹。
注意:對于任意的二叉樹都是由以下幾種情況復合而成的:
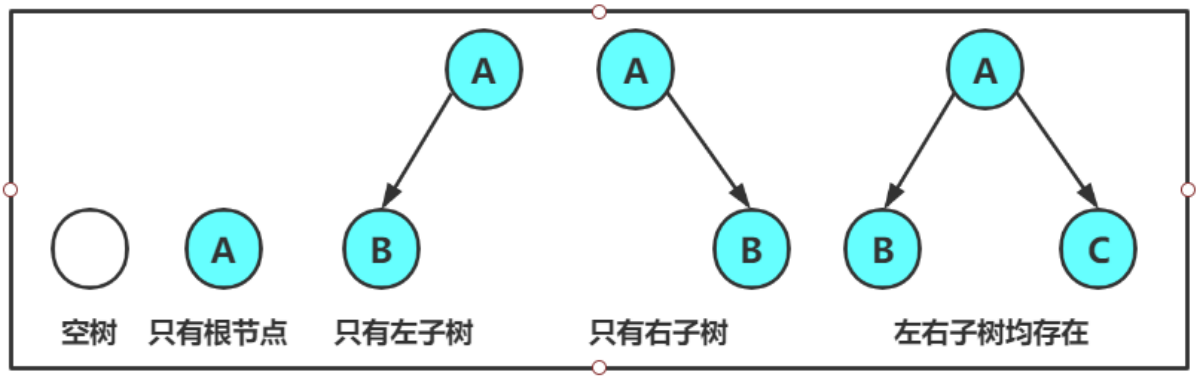
2、現實生活中的二叉樹


3、特殊的二叉樹
- 滿二叉樹:一個二叉樹,如果每一個層的結點數都達到最大值,則這個二叉樹就是滿二叉樹。也就是說,如果一個二叉樹的層數為 K,且結點總數是 2^K-1,則它就是滿二叉樹。
- 完全二叉樹:完全二叉樹是效率很高的數據結構,完全二叉樹是由滿二叉樹而引出來的。對于深度為?K 的,有 n?個結點的二叉樹,當且僅當其每一個結點都與深度為?K?的滿二叉樹中編號從?1?至?n?的結點一一對應時稱之為完全二叉樹。 要注意的是滿二叉樹是一種特殊的完全二叉樹。前 K?層都是滿的,最后一層不一定滿,但最后一層從左到右必須是連續的。深度為 K?的完全二叉樹的節點個數最多為 2^K?- 1,最少為 2^(K-1) - 1 + 1(前 K 層結點個數總和 +1,因為第 K 層至少有一個結點),所以節點個數范圍是:[ 2K-1, 2K?- 1 ]。
4、二叉樹的性質?
- 若規定根節點的層數為?1,則一棵非空二叉樹的第 i 層上最多有 2^(i-1)?個結點。
- 若規定根節點的層數為?1,則深度為?h?的二叉樹的最大結點數是 2^h-1。
- 對任何一棵二叉樹, 如果度為?0?其葉結點個數為 n?, 度為?2?的分支結點個數為 m?,則有?n= m+1。
- 若規定根節點的層數為?1,具有?n?個結點的滿二叉樹的深度,h= log(n+1). (ps:log(n+1)是?log?以?2 為底,n+1 為對數)。
- 對于具有?n?個結點的完全二叉樹,如果按照從上至下從左至右的數組順序對所有節點從 0 開始編號,則對于序號為 i 的結點有: ??????????????
?
- 若?i>0,i 位置節點的雙親序號:(i-1)/2;i=0,i?為根節點編號,無雙親節點。
- 若?2i+1<n,左孩子序號:2i+1,2i+1>=n 否則無左孩子。
- 若?2i+2<n,右孩子序號:2i+2,2i+2>=n 否則無右孩子。
5、二叉樹的存儲結構
二叉樹一般可以使用兩種結構存儲,一種順序結構,一種鏈式結構。
(1)順序存儲
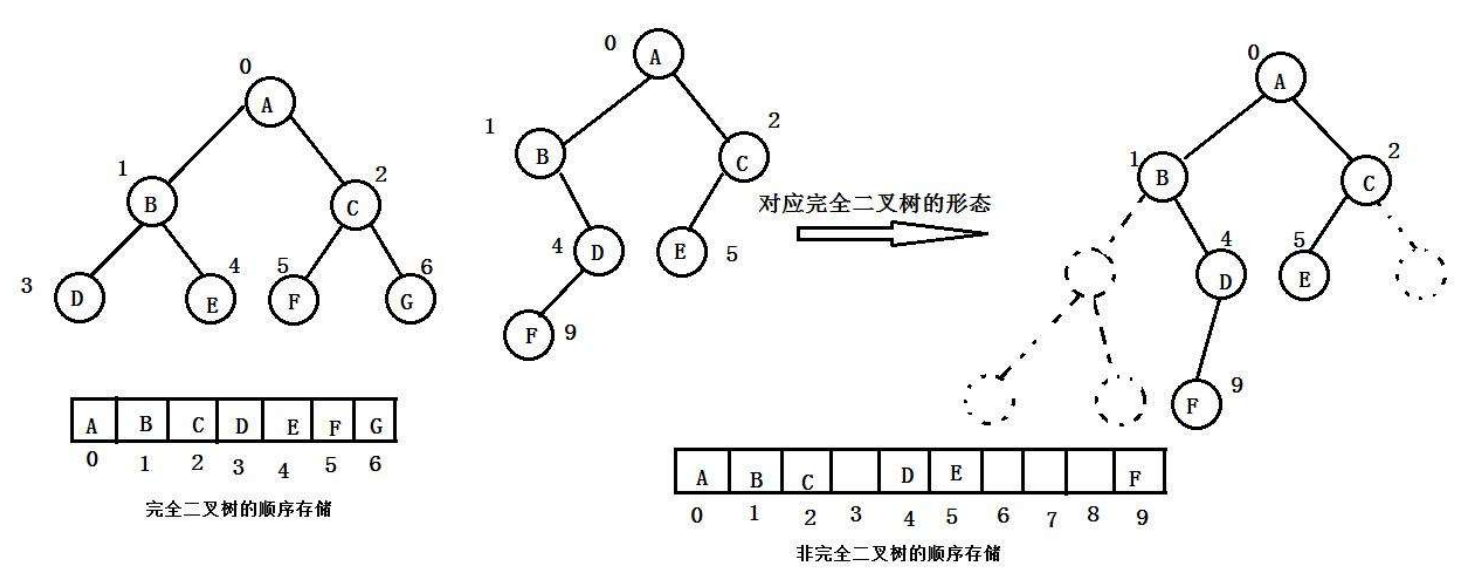
順序結構存儲就是使用數組來存儲,一般使用數組只適合表示完全二叉樹。因為不是完全二叉樹會有空間的浪費。而現實中使用中只有堆才會使用數組來存儲。二叉樹順序存儲在物理上是一個數組,在邏輯上是一顆二叉樹。
leftchild = parent * 2 + 1
rightchild = parent * 2 + 2
parent = (child - 1) / 2
(2)鏈式存儲
二叉樹的鏈式存儲結構是指,用鏈表來表示一棵二叉樹,即用鏈來指示元素的邏輯關系。 通常的方法是鏈表中每個結點由三個域組成,數據域和左右指針域,左右指針分別用來給出該結點左孩子和右孩子所在的鏈結點的存儲地址 。鏈式結構又分為二叉鏈和三叉鏈。目前我們一般用到的都是二叉鏈。( 后面的 數據結構內容如紅黑樹等會用到三叉鏈)
?
typedef int BTDataType;// 二叉鏈
struct BinaryTreeNode
{struct BinaryTreeNode* left; // 指向當前節點左孩子struct BinaryTreeNode* right; // 指向當前節點右孩子BTDataType data; // 當前節點值域
}// 三叉鏈
struct BinaryTreeNode
{struct BinaryTreeNode* parent; // 指向當前節點的雙親struct BinaryTreeNode* left; // 指向當前節點左孩子struct BinaryTreeNode* right; // 指向當前節點右孩子BTDataType data; // 當前節點值域
};