排序算法之快速排序詳解

一、算法介紹

快速排序：快速排序的基本思想是通過一次排序將等待的記錄分成兩個獨立的部分，其中一部分記錄的關鍵字小于另一部分的關鍵字。C部分的快速排序一直持續到整個序列被排序。

任取一個元素 (如第一個) 為中心
提出所有小于它的元素，并將大于它的元素放回，形成左右兩個子表。
為每個子表重新選擇中心元素，并根據此規則進行調整，直到每個子表只剩下一個元素

①每次行程的子表是由兩端到中間的交替近似形成的。

②由于每個子表的操作在每次行程中都是相似的，所以可以使用遞歸算法。

二、基本步驟

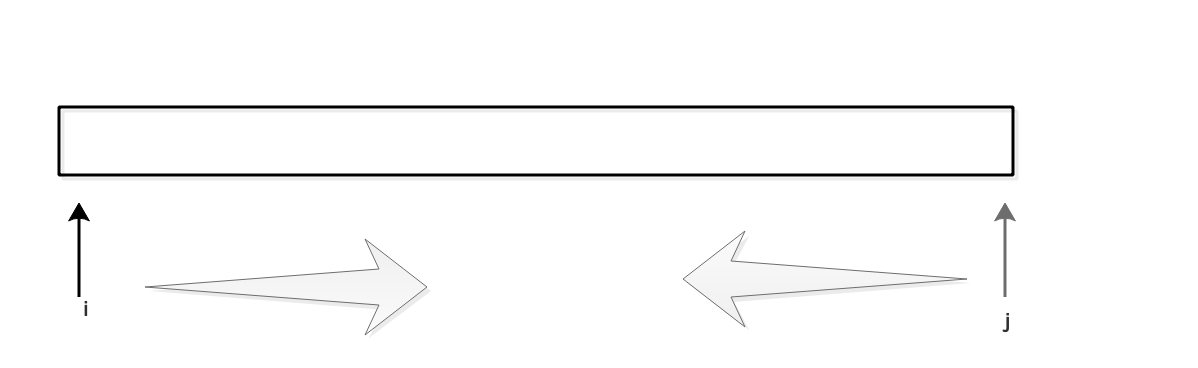
設置兩個指針i，j，首先在序列中選擇一個.temp，并將數字J點與temp進行比較。如果它大于溫度，它將減少1。如果它小于TEMP，則應該取高于當前位置J的值。

三、算法分析

最好：劃分后，左側右側子序列的長度相同,

最壞：從小至大，遞歸樹變成一棵樹。每個分區只能得到一個對象的子序列小于前一個。它必須通過n-1次來定位所有對象，第二次需要通過n-i鍵代碼比較來找到第二個對象的位置。

?

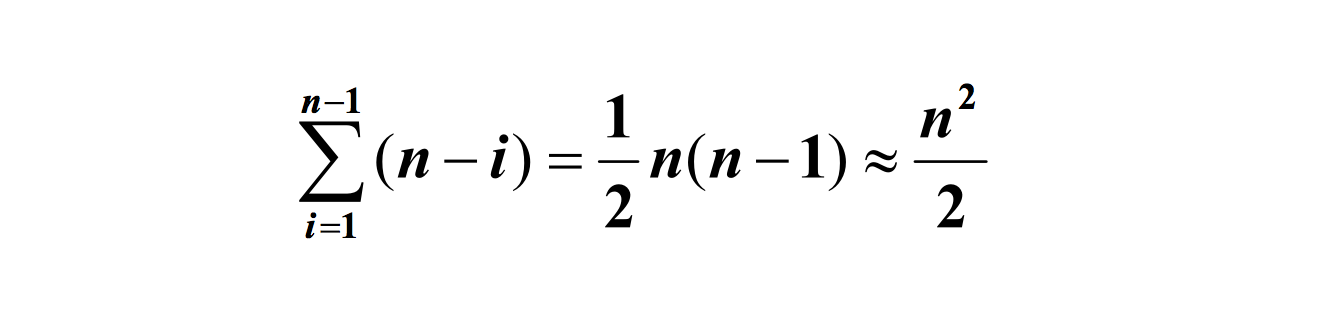
如果所有可能的置換的概率相同，則優選最佳情況和最壞情況平均值。

時間效率：O(nlog2n) —每趟確定的元素呈指數增加
空間效率：O（log2n）—遞歸要用到棧空間
穩 定 性： 不穩定 —可選任一元素為支點

1.如何選樞紐

從上面的描述中可以看出，快速排序是通過樞軸點來回交換的，因此快速排序的分類次數與初始序列有關。
因此，選擇快速分選的關鍵點非常重要，因為它關系到分選的效率。

取前或后法：序列中的第一個或最后一個元素用作基準，如果輸入序列（上面的數組）是隨機的，則處理時間是可接受的。如果數組已經被排序，那么分區就是一個非常糟糕的分區。由于每個分區只能減少要排序的序列，所以這是最壞的情況，并且時間復雜度為_(n^2)。此外，輸入數據排序或部分排序是很常見的。因此，使用第一個元素作為中心元素是非常糟糕的。

隨機選取基準：
這是一個相對安全的策略。因為樞軸的位置是隨機的，所以得到的分割不會總是產生不好的分割。當整個陣列相同時，仍然是最壞的情況，并且時間復雜度為O（n2）。因此，對于大多數輸入數據，隨機快速排序可以達到O（nlogn）的預期時間復雜度。

三數取中法：在快速排隊過程中，每次我們以一個元素作為支點值，用該數將序列分成兩部分。本文采用三位數法，即以左、中、右三位數作為關鍵值，然后進行排序。顯然，三位數的中值分割方法消除了預排序輸入的不良情況，并將快速隊列的比較次數減少了大約14%。

2.如何證明時間復雜度

1、最優情況

在最佳情況下，分區平均每次分區。如果對n個關鍵字進行排序，則遞歸樹的深度為[log2n]+1([x]表示不大于x的最大整數)。也就是說，只需要2次遞歸日志，所需的時間是t（n）。第一個分區應該掃描整個陣列一次。n次比較。然后，獲得的樞軸將陣列分成兩部分，因此每個部分需要T(n/2)時間(注意，最佳情況是，所以分成兩半)。結果，作為連續劃分的結果，作出了以下不等式推斷：
這表明，在最佳情況下，快速排序算法的時間復雜度為O（nLogn）。

2.最壞情況

然后看看快速調度的最壞情況，當要排序的序列是正序或反序時，并且每個分區只產生比前一個分區少一個記錄子序列，注意另一個是空的。如果繪制遞歸樹，則它是傾斜樹。此時需要執行n‐1次遞歸調用，且第i次劃分需要經過n‐i次關鍵字的比較才能找到第i個記錄，也就是樞軸的位置，因此比較次數為n(n-1)/2，最終其時間復雜度為O(n^2)。

3.平均時間復雜度

直接設對規模的數組排序需要的時間期望為, 期望其實就是平均復雜度換個說法.
空表的時候不用排, 所以初值條件就是 T(0) = 0 .所謂快排就是隨便取出一個數,一般是第一個數,然后小于等于他的放左邊, 大于他的的排右邊.比如左邊 k 個那接下來還要排: T(n - k) + T (k - 1) 的時間.然后 k 多少那是不確定的, 遍歷 1~ n , 出現概率都是相等的. 另外分割操作本身也要時間 P(n) , 操作花費是線性時間 P(n) = cn , 這也要加進去, 所以一共是:

四、完整代碼示例

public class QuickSort {

    //任取一個元素 (如第一個) 為中心
    //所有比它小的元素一律前放，比它大的元素一律后放，形成左右兩個子表；
    //對各子表重新選擇中心元素并依此規則調整，直到每個子表的元素只剩一個
    //一趟排序過程后我們返回樞紐的位置
    int partition(int A[], int left, int right) {
        //選擇樞紐元素
        int p = A[left];
        while (left < right) {
            //如果尾指針位置的數比樞紐數要大，移動尾指針的位置，否則就把所指示的值給首指針的位置
            while (left < right && A[right] >= p) {
                --right;
            }
            A[left] = A[right];
            //如果首指針位置的數比樞紐數要小，移動首指針的位置，否則就把所指示的值給尾指針的位置
            while (left < right && A[left] <= p) {
                ++left;
            }
            A[right] = A[left];
        }
        //此時的首尾指針已經相等，把樞紐的值賦給首尾指針相等的位置即可
        A[left] = p;
        return left;
    }

    //快速排序的遞歸
    void Quick(int A[], int left, int right) {
        //定義一個樞紐的位置
        int pnode;
        if (left < right) {
            pnode = partition(A, left, right);
            Quick(A, left, pnode - 1);
            Quick(A, pnode + 1, right);
        }
    }

    public static void main(String[] args) {

    }

?