?
?
---這里記錄下一些關于牛頓法來作為優化器的個人筆記 ：）
關于牛頓法，先不說其中的概念，來簡單看一個例子？ 不用計算器，如何手動開一個值的平方根，比如計算{sqrt(a) | a=4 } ？ 不用程序和代碼如何求？
----比較簡單有木有，直接上用公式來套就好了.
xt = ( xt-1?+ ( a / xt-1?) ) / 2
我們看 sqrt(4) 這個值的區間在1<=sqrt(4)<=4里，寫成這種形式吧[1,4],我們令x0 = 1,
x?= ( 1 + (4/1))/2 = 5/2 =2.5
x = (2.5 + (4/2.5))/2 = 2.05
x = (2.05 + ( 4 /2.05 ))/2 = 2.0006?
.....
? ? 于是我們就求出x的近似值為2
那么這個公式是如何得來的呢？
這個公式其實是依據牛頓法得來的？牛頓法長成什么樣子呢？
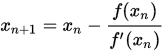?就是長成這個樣子，我們發現這個樣子和我們的SGD還是很像的，這兩者的區別記錄在后面吧～。
而牛頓迭代法，這個公式其實就是泰勒級數展開的前幾項 f(x)，并使得f(x) =0，求解后的結果，而泰勒級數是采用無限項的來等價表示一個函數，比如：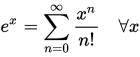
，那牛頓法采用的是泰勒級數的前幾項 -- 有限的項，來近似表示一個函數f(x).
那么如何上面這個公式是如何通過牛頓法得到的呢？
上面的題，我們將其轉換車更加通用的一些，比如改為如何求解sqrt(a)??
?------這又等價于sqrt(a)=x ?轉換成--> ?x^2 = a , (a 屬于實數域)， ?進一步轉換成--->f(x) = x^2 -a =0
我們知道 f(x) = x^2 - a =0 ，因為只要求某一個點的值，所以我們只需要知道這個點的切線就可以了， 由此我們依據泰勒級數定義，對其進行一階展開，可以知道 f(x) ～g(x) = ?f(x0) + f ' (x0)*(x - x0),我們令g(x)=0
于是我們就得到了 x = x0 - f(x0) / f '(x0);
然后我們再次化解這個公式：
x = x0 - (x0^2 - a / 2x0 ) ?= (x0^2 + a) /2x0 ?= (x0 + a/x0)/2
? ? ? 這樣我們就得到了最開始的那個公式了。
但是我們在用牛頓法作為優化器的時候，是要求極小值的啊？ 那么如何快速的求出極小值呢？
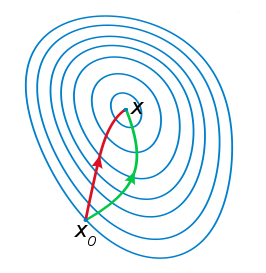
我們知道一階導，為曲線切線方向，二階導為切線的切線方向回想一下SGD法，SGD只是在一階導上，進行權值更新，基本上就是處于求切線方向，前進一個步長，然后再矯正，再求當前點的切線，再矯正：
?
這種方式就會出現綠線的情況，那么牛頓法就給出另一種思路： 我們再沿著切線方向走的時候，不必按照固定的步長走動，我們可以依據切線的變化率來動態調整行走的步子，于是就有了這個公式：
?當二階導趨近于0的時候，說明一階導有極小值，那么此時就應該讓它接近這個極小值，而loss函數為凸函數 ，f’(x)趨近極小值的時候，f(x)就也就可以快速的接近極小值，而不出現大幅度搖擺，就出現了紅色那條線.
一般來說，對于那種高階多項式采用牛頓法效果會比SGD好些.
?
