機器學習（一）—— 線性回歸
目錄
0.?回歸（Regression）的由來
1.?回歸關系
2.?線性回歸的整體思路
（1）根據數據提出假設模型
（2）求解參數
? ? ? 1）梯度下降法
? ? ? 2）正規方程求解參數
（3）梯度下降法與正規方程比較
3.?回歸的一般方法
4. 實例分析
5.?線性回歸的特點及其優缺點
6. 代碼實現（Java）
?
（本文是基于吳恩達老師的機器學習課程整理的）
?
0.?回歸（Regression）的由來
?
*********************************“回歸”一詞的來源************************************
今天所知道的回歸是由達爾文（Charles Darwin）的表兄弟Francis Galton發明的。Galton于1877年完成了第一次回歸預測，目的是根據上一代豌豆種子（雙親）的尺寸來預測下一代豌豆種子（孩子）的尺寸。Galton在大量對象上應用了回歸分析，甚至包括人的身高。他注意到，如果雙親的高度比平均高度高，他們的子女也傾向于比平均高度高，但尚不及雙親。孩子的高度向著平均高度回退（回歸）。Galton在多項研究上都注意到這個現象，所以盡管這個英文單詞跟數值預測沒有任何關系，但這種研究方法仍被稱為回歸。
******************************************************************************************
Regression有“衰退，退步”的意思，Galton在研究父母身高和子女身高時發現，即使父母的身高相對于人群平均身高來說很高，子女的身高比平均值高，但是卻比父母低，即有種向平均值（正常身高）靠近（“衰退”）的傾向。
具體地，Galton和他的學生Pearson在研究父母身高（單位：英寸）與其子女身高的遺傳問題時，觀察了1078對夫婦，以每對夫婦的平均身高作為x，而取他們的一個成年兒子的身高作為y，將結果在平面直角坐標系上繪成散點圖，發現趨勢近乎一條直線，計算出的回歸直線方程為y=33.73+0.516x。這種趨勢及回歸方程總的表明父母平均身高x每增加一個單位，其成年兒子的身高y也平均增加0.516個單位。這個結果表明，雖然高個子父輩確有生高個子兒子的趨勢，但父輩身高增加一個單位，兒子的身高僅增加半個單位左右。反之，矮個子父輩確有生矮個子兒子的趨勢，但父輩身高減少一個單位，兒子身高僅減少半個單位左右。即子代的平均高度向中心回歸了。
?
?1.回歸關系
?
在客觀世界中普遍存在著變量之間的關系，變量之間的關系一般來說可以分為兩種：
①確定性的：變量之間的關系可以用函數關系來表達；
②非確定性的：即統計關系或相關關系。如，人的身高與體重的關系，一般來說人高一些，體重也要重一些，但是也存在同樣高度的人，體重有高有低，即沒有明確的函數關系。現代統計學中關于統計關系已形成兩個重要的分支，它們叫相關分析和回歸分析。
?
回歸分析就是研究統計關系的一種數學工具，能幫助我們從一個變量（預測變量或回歸變量，可以理解為自變量）取得的值去估計另一個變量（響應變量，可以理解為因變量）所取的值。且自變量與因變量均為連續變量。當自變量只有一個變量時，我們稱該回歸為一元回歸，當自變量有多個變量時，稱為多元回歸。若使用線性函數刻畫自變量和因變量之間的相關關系，則稱為線性回歸，否則稱為非線性回歸。所以模型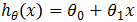
，稱為一元線性回歸模型（或簡單線性回歸模型），模型
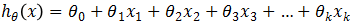，稱為多元線性回歸模型，其中，參數θ0稱為回歸常數，θ1, θ2, … ,θk稱為回歸系數。注意，其中“線性”是用來表明模型的參數θ0, θ1, θ2, …, θk是線性的，而非y是關于x的線性函數。許多模型中y與x以非線性形式相關，但只要方程關于θ是線性的（也就是說不管x是幾次方，只要所有參數θ均為一次方）就仍然可以將其當做線性回歸方程處理，因為當回歸變量為非線性時，可以通過變量替換將它轉化為線性的。
?
需要注意的是：回歸模型并非意味著變量間存在因果關系。即使兩個或更多變量間可能存在牢固的實證關系，也不能認為這就證明了回歸變量與響應變量間存在因果聯系。確立因果關系，要求回歸變量與響應變量必須存在一種基礎性的、與樣本數據無關的關系，比如理論分析中所暗含的關系。回歸分析有助于因果關系的確認，但不能成為判斷因果關系是否存在的唯一基礎。
?
一定要記住，回歸分析只是眾多用于解決問題的數據分析方法的一種，也就是說，回歸方程本身可能并非研究的主要目的，就整個數據處理過程而言，洞察力與理解力通常更為重要。
?
?2.?線性回歸的整體思路
?
（1）根據數據提出假設模型
上面已經知道，回歸的目的是通過幾個已知數據來預測另一個數值型數據的目標值。下面通過例子闡述線性回歸的思想及過程。
假設我們有如下表1所示的訓練集，其中自變量x為房子的面積（單位feet2），因變量為房子的賣價（單位$1000），共有M個樣本。
表 1 ?訓練集樣本（M個樣本）
| size in feet2?(x) | price($) in 1000`s (y) |
| 2104 | 460 |
| 1416 | 232 |
| 1534 | 315 |
| 852 | 178 |
| … | … |
通過觀察，我們發現，隨著x增大，相應的y也增大，所以我們設想x和y應該滿足線性關系，即假設模型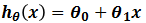
可以描述x和y之間的線性關系，其中θ0，θ1為模型的參數。接下來只需要求解出參數θ0，θ1，就可以為新樣本x`預測相應的房價hθ(x`)，即y`。
?
（2）求解參數
使用回歸分析的一個重要目標是估計模型中的未知參數，這一過程也稱為模型擬合數據。
1）梯度下降法
?
求解參數的原則
模型有了，就差參數了，那該如何求解呢？我們先看看求解參數θ0，θ1，的原則是什么。因為模型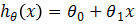
描述的是x和y之間的關系，即越能準確的刻畫x與y的關系，那么模型越好，那怎么來判斷是否準確呢？若對于每一個x，模型預測出的hθ(x)=y，那么無疑該模型非常好，因為它能準確的反應我們訓練集中所有樣本的情況，若是對于未知的x，也能準確的預測出相應的y，那么該模型堪稱完美。可惜這種情況是不存在的，因為在我們收集數據時，會由于各種各樣的原因，造成數據誤差（如測量誤差）或者包含噪聲等后果，所以模型達不到hθ(x)=y這種理想情況，通常hθ(x)-y≠0，我們當然希望這個差值越小越好，那就要調整hθ(x)，所以就需要調整θ0，θ1，到這就明白了，調整參數θ0，θ1的目的（原則）是使模型預測值更接近真實值y，即使差值更小。
?
代價函數（cost?function）
接下來我們需要衡量模型預測值與真實值之間的差異，通過直接求差值hθ(x)-y來計算一個樣本的差是可以的，但是要衡量整個訓練集的差異就會存在正負相抵消的問題，那么用絕對值呢？絕對值沒有正負抵消問題，但是在后面的計算中求導是分段函數，相對比較麻煩，所以也不用。考慮差值的次方，因為奇數次方都會存在正負抵消問題，所以來看偶數次方，偶數次方沒有之前的那些問題，但是考慮到計算的簡便性，我們用平方來計算二者之間的差異，即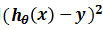
，也稱該函數為平方損失函數。同時，平方損失函數還有個好處是可以懲罰那些差值較大的項，比如(10-5)2=25，(10-8)2=4，25:4相較于5:2更能突出差異大的點。
?
接下來，我們用平方損失函數對每一個樣本計算差異（損失），再求和取平均作為整體訓練集對參數θ0，θ1的損失J(θ0, θ1)，公式為：
，其中公式中的1/2是為了后續求導計算中約掉指數上的2，x(i)，y(i)表示第i個樣本。我們稱J(θ0, θ1)為代價函數（cost function），其反映了訓練集所有樣本在參數θ0，θ1下的平均損失。因為我們需要模型能較為準確的表示變量之間的關系，也即模型預測值與真實值之間的差異要盡可能的小，所以我們需要J(θ0, θ1)盡可能的小，也就是說，現在將從假設模型
中直接求參數θ0，θ1轉化為在代價函數J(θ0, θ1)中求解參數θ0，θ1，使代價函數J(θ0, θ1)最小。
??
代價函數J(θ0, θ1)和模型hθ(x)之間的關系
? 首先模型hθ(x)是給定參數θ下，關于x的函數，而J(θ0, θ1)是關于θ0，θ1的函數。給定參數θ0，θ1，可以計算出一個J(θ0, θ1)。為了方便表示和理解，我們假設參數θ0=0，即模型是過原點的直線，設樣本點為(1, 1), (2, 2), (3, 3)，接下來，我們取不同的θ1來計算J(θ1)。
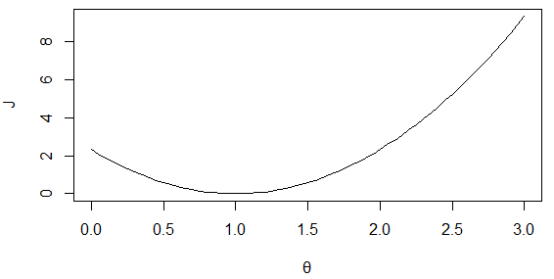
如下圖1所示，黑色線表示θ1=1，三個樣本點剛好全都落在該直線上，其代價函數值為0，所以J(θ1)過點(1, 0)，藍色直線斜率為0.5，其代價函數值為0.58，所以J(θ1)過點(0.5, 0.58)，同樣綠色直線斜率為2，其代價值為7/3，所以J(θ1)過點(2, 7/3)，得到的代價函數如圖2所示。若不設θ0=0，則J(θ0, θ1)的等高線如圖3所示。
?
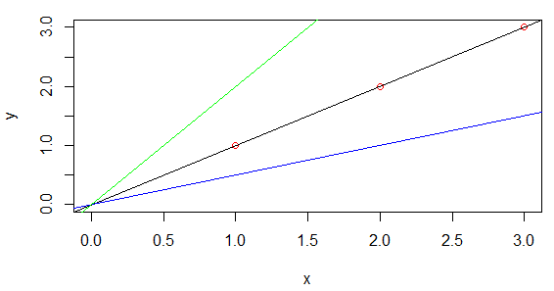
圖 1 不同參數下的模型
?
?
圖 2 代價函數J(θ1)
?
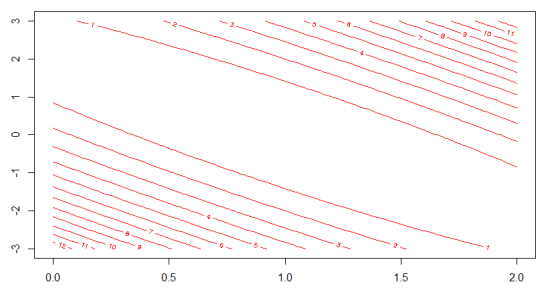
圖 3 J(θ0, θ1)的等高線，橫軸為θ1，縱軸為θ0
利用代價函數求解參數
我們的目的是求得參數θ0，θ1，使代價函數J(θ0, θ1)值最小。即
，因為線性回歸的代價函數J(θ)總是凹面，即凸函數，最小化J(θ)屬于凸優化，我們用最經典的梯度下降算法。
梯度下降法的思路：
- 給參數θ0，θ1初始值，常設為（0,?0）
- 調整θ0，θ1使J(θ0, θ1)減小
- 直到代價函數J(θ0, θ1)減小到最小值
為什么要設置初始值為0呢？因為后續都會調整參數來求代價函數的最小值，而且先前我們也不知道要具體設置為多少，所以遵循簡單原則，設置為0。接下來調整參數，如下：
重復以下步驟直到收斂{
}
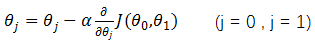
α為下降步長，也叫學習率（learning rate），它決定了在梯度下降迭代的過程中，每一步沿梯度負方向前進的長度。偏導數項是用來保證以直線方向下降（最快下降方向）。
我們來看看α產生的影響，同樣的，設θ0=0，在之前圖2中會產生以下收斂方式，因為J(θ)圖形變化比較緩慢，所以會隨著導數項減小而減小，如圖4所示，經多次減小后，越到最小值附近，J(θ)變化越緩慢。但是對于圖5來說，J(θ)比較陡峭，變化較快，在接近最低點的時候導數值依然很大。即α過大，可能會引起振蕩，找不到極值點，α過小，會導致收斂時間太長。那么要怎么選取合適的α呢？吳恩達老師給的建議是從[0.001, 0.003, 0.01, 0.03, 0.1, 0.3…]中選擇。在實驗過程中可以通過判斷第i次更新后的代價值是否小于第i-1次，若小于，可以稍微增大一點α，以更快的收斂；若大于，則需要減小α，防止發生振蕩。
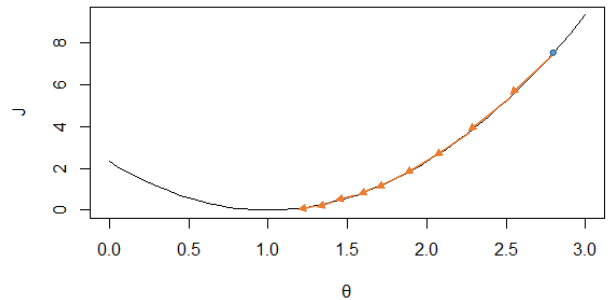
圖 4 變換緩慢的J(θ)上的收斂過程
?
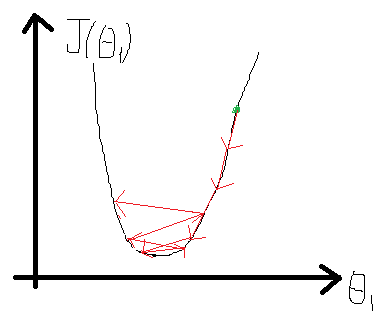
圖 5 比較陡峭的J(θ)上的收斂過程
接下來，我們用一個例子說明梯度下降方法。求y=(x-1)2的最小值點，選步長為0.5：
①?設初始值x0=0，則y=1，在x=0處梯度值為-2，
②?更新x1=0-0.5*(-2)=1，則y=0，此處梯度值為0，找到最小值點（1,0）
接下來我們如何判斷收斂呢？對于一般的數學函數來說，只要導數值為0即可，但是對于1/x這類函數來說，有兩種方式來判斷其是否收斂，一種是看J(θ)的函數圖形，如果基本沒有變化，則可認為是收斂；另一種為設置變化閾值ε，如ε<0.001，若兩次相鄰的J(θ)變化小于ε，則可認為是收斂了，但是如何確定ε的大小則比較困難。
?
多元線性回歸
之前描述的是一元線性回歸，那么如何對多元變量進行線性回歸呢？如下表2的訓練數據：
表2 多維特征數據
| size (feet2) ?x1 | number of bedrooms ?x2 | number of floors??x3 | age of home ? x4 | price($1000) y |
| 2104 | 5 | 1 | 45 | 460 |
| 1416 | 3 | 2 | 40 | 232 |
| 1534 | 3 | 2 | 30 | 315 |
| 852 | 2 | 1 | 36 | 178 |
| … | … | … | … | … |
此時假設模型函數為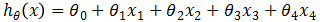
，代價函數：
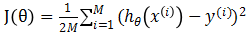，其中θ為5維向量，優化與求解與之前一樣。
需要注意的是，因為特征中x1, x2之間的取值范圍差異太大，得到的J(θ)性狀窄長（因為取值范圍一大一小），會導致收斂產生振蕩，如下圖6所示（手畫，比較丑）。
?
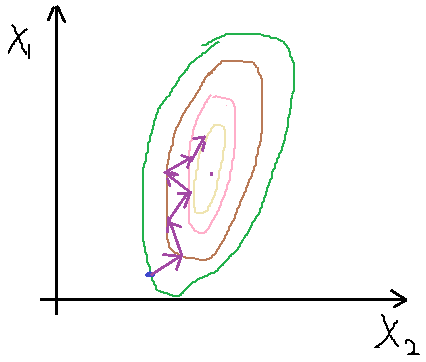
圖 6 特征取值范圍較大時會出現振蕩
產生振蕩會使收斂不到最小點處，因此為了避免這種情況，我們需要對特征進行縮放，也相當于歸一化處理，使他們的取值范圍都在一個區間，通常我們將特征值除以該特征的最大值與最小值的差。比如若x1取值范圍為650--3000，縮放為：x1/(3000-650)。縮放后代價函數變得相對圓些，如圖7?所示，其收斂過程就相對平滑，也能較快收斂到最小值點。
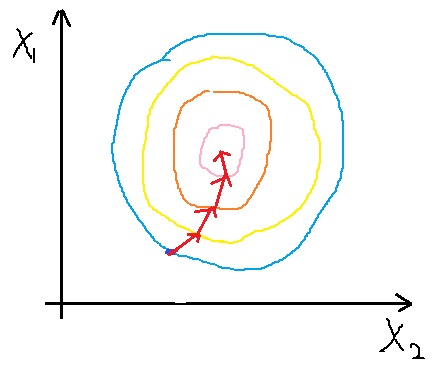
圖 7 特征縮放后的收斂相對平緩
2）正規方程求解參數
對于表2中的數據，我們添一列x0，使其全為1，模型寫為：hθ(x)?= θ0x0+θ1x1+θ2x2+θ3x3+θ4x4。我們記矩陣
?
其中，每一行為一個樣本的所有特征，X稱為設計矩陣（design matrix），為m*(n+1)型矩陣，其中m是訓練集樣本數，n為樣本的特征數（不包括x0）。記向量y=(460, 232, 315, 178, …)T，即y為m*1型，同樣記θ=(θ0, θ1，θ2, θ3, θ4)為（n+1）*1型，類似于梯度下降的優化目標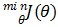
，有
，令Eθ=(y-Xθ)T(y-Xθ)，對θ求導得到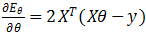
，令其為0，可得到θ的最優解，θ=(XTX)-1XTy，但是XTX的逆是否一直存在呢？其實不是的，當矩陣X中存在冗余的特征，那么就不可逆，還有，當m≤n，即特征數太多，對于這兩種情況，都可以通過刪除特征解決，對于冗余特征來說，我們刪除掉冗余的特征，第二種情況除過刪除特征外，還可以使用正則化的方式解決： θ=(XTX+λB)-1XTy，其中B為(n+1)*(n+1)型矩陣，其對角線上除B11外均為1，其余為0，則括號內的矩陣絕對可逆。
?
（4）梯度下降法與正規方程比較
| 梯度下降法 | 正規方程 |
| 需要選擇學習率（下降步長）α | 不需要選擇α |
| 需要多次迭代 | 不需要迭代，一次運算得出 |
| 當特征數量N很大時，依然能很好的運用 | 需要計算（XTX）的逆，若特征數量N很大時，計算代價太大，求矩陣逆復雜度為O(n3) |
| 適用于各種類型的模型 | 只適用于線性模型，不適合邏輯回歸模型等其他模型 |
?
?3.?回歸的一般方法
?
（1）?收集數據：采用任意方法收集數據；
（2）?準備數據：回歸需要數值型數據，標稱型數據將被轉成二值型數據；
（3）?分析數據：繪出數據的可視化二維圖將有助于對數據做出理解和分析，在采用縮減法求得新回歸系數之后，可以將新擬合線繪在圖上作為對比；
（4）?訓練算法：找到回歸系數；
（5）?測試算法：使用R2或者預測值和數據的擬合度，來分析模型的效果；
（6）?使用算法：使用回歸，可以在給定輸入的時候預測出一個數值，這是對分類方法的提升，因為這樣可以預測連續型數據而不僅僅是離散的類別標簽。
?
?4.?實例分析
為了可視化效果，我們只使用一個特征（size?of feet2）來說明線性回歸的實例應用。
（1）?收集數據：我們根據現實生活的情況，設定了20個樣本，如下表3所示：
表3 訓練樣本集
| Size?of feet2 | Price ($1000) |
| 2104 | 460 |
| 1416 | 232 |
| 265 | 32 |
| 568 | 98 |
| 1564 | 250 |
| 100 | 23 |
| 3645 | 564 |
| 879 | 125 |
| 356 | 86 |
| 873 | 105 |
| 1356 | 254 |
| 458 | 36 |
| 1587 | 298 |
| 2458 | 521 |
| 2478 | 512 |
| 3578 | 652 |
| 458 | 87 |
| 965 | 154 |
| 546 | 65 |
| 1548 | 246 |
?
（2）?準備數據：數據已是數值型數據；
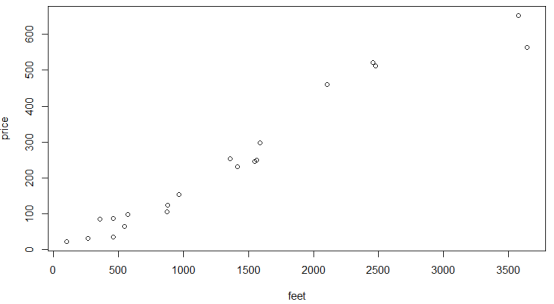
（3）?分析數據：將其可視化如下圖8.
?
圖8 訓練集數據的可視化
（4）?訓練算法：
我們的假設為hθ(x)=θ0+θ1*x，優化的目標函數為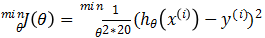
?，根據梯度下降法，通過判斷參數更新前后的代價函數差值來看是否α取得過大，即差值小于零，表示更新完參數后，代價值增加，說明有振蕩產生，因此再減小α。經過試驗，取學習率（下降步長）為10^-6，當連續兩次代價函數差小于10^-6作為收斂條件，求得θ0=-10.13，θ1=0.18，此時的代價J(θ)=890.81
（5）?測試算法：
我們將得到的hθ(x)與樣本點畫出來，如下圖9.可以看出效果不錯，畢竟事實就是房子面積越大，賣價越高，當然還有地段等因素影響，所以并不是完全都在直線上。
?
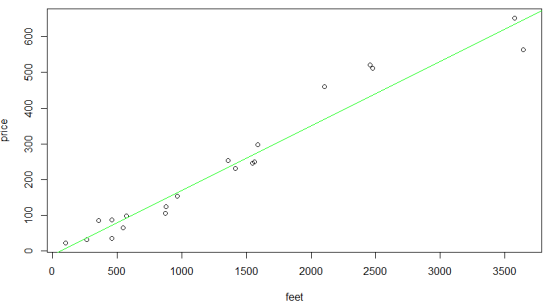
圖 9 樣本點與回歸線
（6）?使用算法：我們用得到的線性模型對新樣本x=2000，來預測該面積的房子賣價y=hθ(x)=-10.13+0.18*2000=349.87，注意單位是千$。
?
5.線性回歸的特點及其優缺點
?
使用數據類型：數值型和標稱型數據
優點：
結果易于理解，計算上不復雜；
可以根據系數理解每個變量；
缺點：
對非線性的數據擬合不好；
對異常值非常敏感；
受噪聲影響大；
只能表示線性關系；
?
?6.?代碼實現（Java）
?https://www.cnblogs.com/datamining-bio/articles/9240378.html
)
 圖片接口與文件上傳)
