先,定義一下 狀態Position P 先手必敗 N x先手必勝
操作方法: 反向轉移
?相同狀態 不同位置 的一對 相當于無
對于ICG游戲,我們可以將游戲中每一個可能發生的局面表示為一個點。并且若存在局面i和局面j,且j是i的后繼局面(即局面i可以轉化為局面j),我們用一條有向邊,從i出發到j,連接表示局面i和局面j的點。則整個游戲可以表示成為一個有向無環圖:
根據ICG游戲的定義我們知道,任意一個無法繼續進行下去的局面為終結局面,即P局面(先手必敗)。在上圖中我們可以標記所有出度為0的點為P點。接著根據ICG游戲的兩條性質,我們可以逆推出所有點為P局面還是N局面:
對于一個游戲可能發生的局面x,我們如下定義它的sg值:
(1)若當前局面x為終結局面,則sg值為0。
(2)若當前局面x非終結局面,其sg值為:sg(x) = mex{sg(y) | y是x的后繼局面}。
mex{a[i]}表示a中未出現的最小非負整數。舉個例子來說:
mex{0, 1, 2} = 3, mex{1, 2}=0, mex{0,1,3}=2
我們將上圖用sg函數表示后,得到: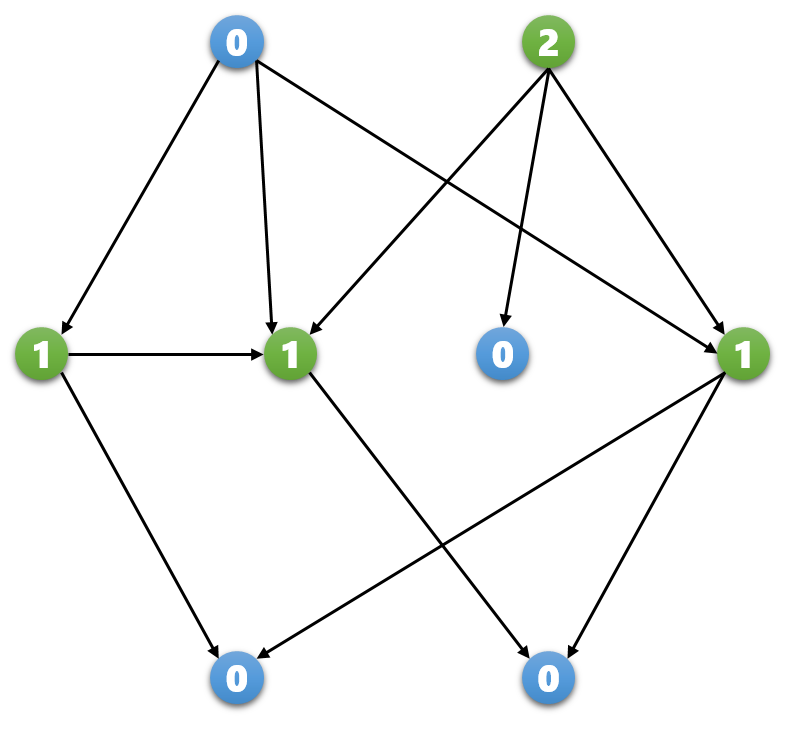
可以發現,若一個局面x為P局面,則有sg(x)=0;否則sg(x)>0。同樣sg值也滿足N、P之間的轉換關系:
若一個局面x,其sg(x)>0,則一定存在一個后續局面y,sg(y)=0。
若一個局面x,其sg(x)=0,則x的所有后續局面y,sg(y)>0。
由上面的推論,我們可以知道用N、P-Position可以描述的游戲用sg同樣可以描述。并且在sg函數中還有一個非常好用的定理,叫做sg定理:
對于多個單一游戲,X=x[1..n],每一次我們只能改變其中一個單一游戲的局面。則其總局面的sg值等于這些單一游戲的sg值異或和。
?
?
先定義mex(minimal excludant)運算,這是施加于一個集合的運算,表示最小的不屬于這個集合的非負整數。例如mex{0,1,2,4}=3、mex{2,3,5}=0、mex{}=0。
對于一個給定的有向無環圖,定義關于圖的每個頂點的Sprague-Grundy函數g如下:g(x)=mex{ g(y) | y是x的后繼 },這里的g(x)即sg[x]
例如:取石子問題,有1堆n個的石子,每次只能取{1,3,4}個石子,先取完石子者勝利,那么各個數的SG值為多少?
sg[0]=0,f[]={1,3,4},
x=1時,可以取走1-f{1}個石子,剩余{0}個,mex{sg[0]}={0},故sg[1]=1;
x=2時,可以取走2-f{1}個石子,剩余{1}個,mex{sg[1]}={1},故sg[2]=0;
x=3時,可以取走3-f{1,3}個石子,剩余{2,0}個,mex{sg[2],sg[0]}={0,0},故sg[3]=1;
x=4時,可以取走4-f{1,3,4}個石子,剩余{3,1,0}個,mex{sg[3],sg[1],sg[0]}={1,1,0},故sg[4]=2;
x=5時,可以取走5-f{1,3,4}個石子,剩余{4,2,1}個,mex{sg[4],sg[2],sg[1]}={2,0,1},故sg[5]=3;
以此類推.....
? ?x ? ? ? ? 0 ?1 ?2 ?3 ?4 ?5 ?6 ?7 ?8....
sg[x] ? ? ?0 ?1 ?0 ?1 ?2 ?3 ?2 ?0 ?1....
?
計算從1-n范圍內的SG值。
f(存儲可以走的步數,f[0]表示可以有多少種走法)
f[]需要從小到大排序
1.可選步數為1~m的連續整數,直接取模即可,SG(x) = x % (m+1);
2.可選步數為任意步,SG(x)?= x;
3.可選步數為一系列不連續的數,用GetSG()計算
?


//f[]:可以取走的石子個數 //sg[]:0~n的SG函數值 //hash[]:mex{} int f[N],sg[N],hash[N]; void getSG(int n) {int i,j;memset(sg,0,sizeof(sg));for(i=1;i<=n;i++){memset(hash,0,sizeof(hash));for(j=1;f[j]<=i;j++)hash[sg[i-f[j]]]=1;for(j=0;j<=n;j++) //求mes{}中未出現的最小的非負整數 {if(hash[j]==0){sg[i]=j;break;}}} }


//注意 S數組要按從小到大排序 SG函數要初始化為-1 對于每個集合只需初始化1遍 //n是集合s的大小 S[i]是定義的特殊取法規則的數組 int s[110],sg[10010],n; int SG_dfs(int x) {int i;if(sg[x]!=-1)return sg[x];bool vis[110];memset(vis,0,sizeof(vis));for(i=0;i<n;i++){if(x>=s[i]){SG_dfs(x-s[i]);vis[sg[x-s[i]]]=1;}}int e;for(i=0;;i++)if(!vis[i]){e=i;break;}return sg[x]=e; }
?注意在SG表的初始化中,不用每次都初始;否則會T的,因為可以循環利用,這是一個強大的地方
HDU1536 實戰


#include<stdio.h> #include<algorithm> #include<string.h> using namespace std; int s[110],sg[10010],n; char op[200]; int SG_dfs(int x) {int i;if(sg[x]!=-1)return sg[x];bool vis[110];memset(vis,0,sizeof(vis));for(i=0;i<n;i++){if(x>=s[i]){SG_dfs(x-s[i]);vis[sg[x-s[i]]]=1;}}int e;for(i=0;;i++)if(!vis[i]){e=i;break;}return sg[x]=e; } int main() {int k;while(scanf("%d",&n)!=EOF){if(n==0)break;for(int i=0 ; i<n ; i++)scanf("%d",&s[i]);sort(s,s+n);int m,cnt=0;scanf("%d",&m);memset(sg,-1,sizeof(sg));for(int i=0 ; i<m ; i++){scanf("%d",&k);int x=0;while(k--){int w;scanf("%d",&w);x^=SG_dfs(w);}if(x!=0)printf("W");elseprintf("L");}puts("");}return 0; }
?














)




