NOIP2009靶形數獨

?

試題描述

小城和小華都是熱愛數學的好學生，最近，他們不約而同地迷上了數獨游戲，好勝的他們想用數獨來一比高低。但普通的數獨對他們來說都過于簡單了，于是他們向 Z 博士請教， Z 博士拿出了他最近發明的“靶形數獨”，作為這兩個孩子比試的題目。
靶形數獨的方格同普通數獨一樣，在 9 格寬 ×9 格高 的大九宮格中有 9 個 3格寬×3 格高 的小九宮格（用粗黑色線隔開的）。在這個大九宮格中，有一些數字是已知的，根據這些數字，利用邏輯推理，在其他的空格上填入 1 到 9 的數字。每個數字在每個小九宮格內不能 重復出現，每個數字在每行、每列也不能重復出現。但靶形數獨有一點和普通數獨不同，即 每一個方格都有一個分值，而且如同一個靶子一樣，離中心越近則分值越高。（如圖）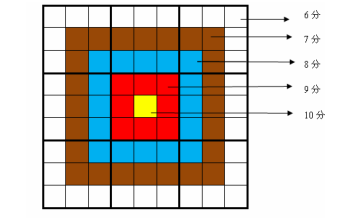






上圖具體的分值分布是：里面一格（黃色區域）為 10 分，黃色區域外面的一圈（紅色區域）每個格子為 9 分，再外面一圈（藍色區域）每個格子為 8 分，藍色區域外面一圈（棕色區域）每個格子為 7 分，外面一圈（白色區域）每個格子為 6 分，如上圖所示。
比賽的要求是：每個人必須完成一個給定的數獨（每個給定數獨可能有不同的填法），而且要爭取更高的總分數。而這個總分數即每個方格上的分值和完成這個數獨時填在相應格上的數字的乘積的總和。
如圖，在以下的這個已經填完數字的靶形數獨游戲中，總分數為 2829 。游戲規定，將以總分數的高低決出勝負。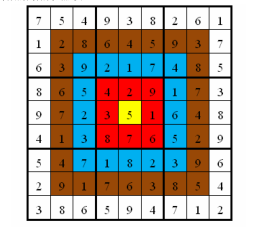


由于求勝心切，小城找到了善于編程的你，讓你幫他求出，對于給定的靶形數獨，能夠得到的高分數。

輸入

輸入一共?9?行。每行?9個整數（每個數都在?
0—9?的范圍內），表示一個尚未填滿的數獨方格，未填的空格用?0?表示。每兩個數字之間用一個空格隔開。

輸出

輸出共?1?行。

輸出可以得到的靶形數獨的高分數。如果這個數獨無解，則輸出整數??1?。

輸入示例

樣例輸入?1
7?0?0?9?0?0?0?0?1
1?0?0?0?0?5?9?0?0
0?0?0?2?0?0?0?8?0
0?0?5?0?2?0?0?0?3
0?0?0?0?0?0?6?4?8
4?1?3?0?0?0?0?0?0
0?0?7?0?0?2?0?9?0
2?0?1?0?6?0?8?0?4
0?8?0?5?0?4?0?1?2
樣例輸入?2
0?0?0?7?0?2?4?5?3
9?0?0?0?0?8?0?0?0
7?4?0?0?0?5?0?1?0
1?9?5?0?8?0?0?0?0
0?7?0?0?0?0?0?2?5
0?3?0?5?7?9?1?0?8
0?0?0?6?0?1?0?0?0
0?6?0?9?0?0?0?0?1
0?0?0?0?0?0?0?0?6?

輸出示例

樣例輸出?1
2829
樣例輸出?2
2852

---

因為我們知道分值是多少，所以可以先打出表格，然后美劇所有的情況，進行判斷，最后加點剪枝就可以過

難點在于如何計算出每個數字在哪個宮，(x-1)/3*3+1+(y-1)/3，x代表行，y代表列

還有就是我們OJ是真的慢，最后只好打表QAQ

#include<iostream>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<algorithm>
#include<queue>
using namespace std;
inline int min(int a,int b){return a<b?a:b;}
inline int max(int a,int b){return a>b?a:b;}
inline int rd()
{int x=0,f=1;char c=getchar();for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;for(;isdigit(c);c=getchar()) x=x*10+c-'0';return x*f;
}
inline void write(int x)
{if(x<0) putchar('-'),x=-x;if(x>9) write(x/10);putchar(x%10+'0');
}
const int score[10][10]={{0,0,0,0,0,0,0,0,0,0},{0,6,6,6,6,6,6,6,6,6},{0,6,7,7,7,7,7,7,7,6},{0,6,7,8,8,8,8,8,7,6},{0,6,7,8,9,9,9,8,7,6},{0,6,7,8,9,10,9,8,7,6},{0,6,7,8,9,9,9,8,7,6},{0,6,7,8,8,8,8,8,7,6},{0,6,7,7,7,7,7,7,7,6},{0,6,6,6,6,6,6,6,6,6}};
int map[100][100],row[100][100],col[100][100],gong[100][100];
int rcnt[10000],ccnt[10000];
int cnt=0;
int ans=-1;
int id(int x,int y){return (x-1)/3*3+1+(y-1)/3;}
int check()
{int sum=0;for(int i=1;i<=9;i++) for(int j=1;j<=9;j++) sum+=(score[i][j]*map[i][j]);return sum;
}
void dfs(int r,int c,int sum)
{if(sum==81){ans=max(ans,check());return ;}for(int k=1;k<=9;k++){if(row[r][k]!=0||col[c][k]!=0||gong[id(r,c)][k]!=0) continue;row[r][k]=1;col[c][k]=1;gong[id(r,c)][k]=1;rcnt[r]++;ccnt[c]++;map[r][c]=k;int rr,tmpr=-1,cc,tmpc=-1;for(int j=1;j<=9;j++){if(rcnt[j]>tmpr&&rcnt[j]<9){tmpr=rcnt[j];rr=j;}}for(int j=1;j<=9;j++){if(ccnt[j]>tmpc&&map[rr][j]==0){tmpc=ccnt[j];cc=j;}}dfs(rr,cc,sum+1);row[r][k]=0;col[c][k]=0;gong[id(r,c)][k]=0;map[r][c]=0;rcnt[r]--;ccnt[c]--;}return ;
}
int main()
{int i,j;for(i=1;i<=9;i++){for(j=1;j<=9;j++){map[i][j]=rd();if(map[i][j]!=0){row[i][map[i][j]]=1;col[j][map[i][j]]=1;gong[id(i,j)][map[i][j]]=1;rcnt[i]++;ccnt[j]++;cnt++;}}}int r,tmpr=-1,c,tmpc=-1;for(i=1;i<=9;i++){if(rcnt[i]>tmpr&&rcnt[i]<9){tmpr=rcnt[i];r=i;}}for(i=1;i<=9;i++){if(ccnt[i]>tmpc&&map[r][i]==0){tmpc=ccnt[i];c=i;}}dfs(r,c,cnt);printf("%d",ans);return 0;
}

?