使用DBSCAN標識為員工分組

照片由Ishan @seefromthesky 在 Unsplash拍攝

基于密度的噪聲應用空間聚類(DBSCAN)是一種無監督的ML聚類算法。無監督的意思是它不使用預先標記的目標來聚類數據點。聚類是指試圖將相似的數據點分組到人工確定的組或簇中。它可以替代KMeans和層次聚類等流行的聚類算法。

在我們的示例中，我們將檢查一個包含15,000名員工的人力資源數據集。數據集包含員工的工作特征，如工作滿意度、績效評分、工作量、任職年限、事故、升職次數。

KMeans vs DBSCAN

KMeans尤其容易受到異常值的影響。當算法遍歷質心時，在達到穩定性和收斂性之前，離群值對質心的移動方式有顯著的影響。此外，KMeans在集群大小和密度不同的情況下還存在數據精確聚類的問題。K-Means只能應用球形簇，如果數據不是球形的，它的準確性就會受到影響。最后，KMeans要求我們首先選擇希望找到的集群的數量。下面是KMeans和DBSCAN如何聚類同一個數據集的示例。

另一方面，DBSCAN不要求我們指定集群的數量，避免了異常值，并且在任意形狀和大小的集群中工作得非常好。它沒有質心，聚類簇是通過將相鄰的點連接在一起的過程形成的。

DBSCAN是如何實現的呢?

首先，讓我們定義Epsilon和最小點、應用DBSCAN算法時需要的兩個參數以及一些額外的參數。

1. Epsilon (?)：社區的最大半徑。如果數據點的相互距離小于或等于指定的epsilon，那么它們將是同一類的。換句話說，它是DBSCAN用來確定兩個點是否相似和屬于同一類的距離。更大的epsilon將產生更大的簇(包含更多的數據點)，更小的epsilon將構建更小的簇。一般來說，我們喜歡較小的值是因為我們只需要很小一部分的數據點在彼此之間的距離內。但是如果太小，您會將集群分割的越來越小。

1. 最小點(minPts)：在一個鄰域的半徑內minPts數的鄰域被認為是一個簇。請記住，初始點包含在minPts中。一個較低的minPts幫助算法建立更多的集群與更多的噪聲或離群值。較高的minPts將確保更健壯的集群，但如果集群太大，較小的集群將被合并到較大的集群中。

如果"最小點"= 4，則在彼此距離內的任意4個或4個以上的點都被認為是一個簇。

其他參數

核心點:核心數據點在其近鄰距離內至少有的最小的數據點個數。

我一直認為DBSCAN需要一個名為"core_min"的第三個參數，它將確定一個鄰域點簇被認為是聚類簇之前的最小核心點數量。

邊界點:邊界數據點位于郊區，就像它們屬于近鄰點一樣。(比如w/在epsilon距離內的核心點)，但需要小于minPts。

離群點:這些點不是近鄰點，也不是邊界點。這些點位于低密度地區。

首先，選擇一個在其半徑內至少有minPts的隨機點。然后對核心點的鄰域內的每個點進行評估，以確定它是否在epsilon距離內有minPts (minPts包括點本身)。如果該點滿足minPts標準，它將成為另一個核心點，集群將擴展。如果一個點不滿足minPts標準，它成為邊界點。隨著過程的繼續，算法開始發展成為核心點"a"是"b"的鄰居，而"b"又是"c"的鄰居，以此類推。當集群被邊界點包圍時，這個聚類簇已經搜索完全，因為在距離內沒有更多的點。選擇一個新的隨機點，并重復該過程以識別下一個簇。

如何確定最優的Epsilon值

估計最優值的一種方法是使用k近鄰算法。如果您還記得的話，這是一種有監督的ML聚類算法，它根據新數據點與其他"已知"數據點的距離來聚類。我們在帶標記的訓練數據上訓練一個KNN模型，以確定哪些數據點屬于哪個聚類。當我們將模型應用到新數據時，算法根據與訓練過的聚類的距離來確定新數據點屬于哪一個聚類。我們必須確定"k"參數，它指定在將新數據點分配給一個集群之前，模型將考慮多少個最鄰近點。

為了確定最佳的epsilon值，我們計算每個點與其最近/最近鄰居之間的平均距離。然后我們繪制一個k距離，并選擇在圖的"肘部"處的epsilon值。在y軸上，我們繪制平均距離，在x軸上繪制數據集中的所有數據點。

如果選取的epsilon太小，很大一部分數據將不會被聚類，而一個大的epsilon值將導致聚類簇被合并，大部分數據點將會在同一個簇中。一般來說，較小的值比較合適，并且作為一個經驗法則，只有一小部分的點應該在這個距離內。

如何確定最佳minPts

通常，我們應該將minPts設置為大于或等于數據集的維數。也就是說，我們經常看到人們用特征的維度數乘以2來確定它們的minPts值。

就像用來確定最佳的epsilon值的"肘部方法"一樣，minPts的這種確定方法并不是100%正確的。

DBSCAN聚類的評價方式

影像法：該技術測量集群之間的可分離性。首先，找出每個點與集群中所有其他點之間的平均距離。然后測量每個點和其他簇中的每個點之間的距離。我們將兩個平均值相減，再除以更大的那個平均值。

我們最終想要的是一種較高(比如最接近1)的分數，表明存在較小的簇內平均距離(緊密簇)和較大的簇間平均距離(簇間分離良好)。

集群可視化解釋:獲得集群之后，解釋每個集群非常重要。這通常是通過合并原始數據集和集群并可視化每個集群來完成的。每個集群越清晰越獨特越好。我們將在下面實現這個過程。

DBSCAN的優點

· 不需要像KMeans那樣預先確定集群的數量

· 對異常值不敏感

· 能將高密度數據分離成小集群

· 可以聚類非線性關系(聚類為任意形狀)

DBSCAN的缺點

· 很難在不同密度的數據中識別集群

· 難以聚類高維數據

· 對極小點的參數非常敏感

讓我們嘗試一下

import numpy as npimport pandas as pdimport matplotlib.pyplot as pltimport seaborn as snsimport plotly.offline as pyopyo.init_notebook_mode()import plotly.graph_objs as gofrom plotly import toolsfrom plotly.subplots import make_subplotsimport plotly.offline as pyimport plotly.express as pxfrom sklearn.cluster import DBSCANfrom sklearn.neighbors import NearestNeighborsfrom sklearn.metrics import silhouette_scorefrom sklearn.preprocessing import StandardScalerfrom sklearn.decomposition import PCAplt.style.use('fivethirtyeight')from warnings import filterwarningsfilterwarnings('ignore')with open('HR_data.csv') as f:    df =  pd.read_csv(f, usecols=['satisfaction_level', 'last_evaluation', 'number_project',       'average_montly_hours', 'time_spend_company', 'Work_accident',       'promotion_last_5years'])f.close()

1. 標準化

由于數據集中的特特征不在相同的范圍內，所以我們需要對整個數據集進行標準化。換句話說，我們數據集中的每個特征對于它們的數據都有獨特的大小和范圍。滿意度水平增加一分并不等于最后評價增加一分，反之亦然。由于DBSCAN利用點之間的距離(歐幾里得)來確定相似性，未縮放的數據會產生問題。如果某一特征在其數據中具有較高的可變性，則距離計算受該特征的影響較大。通過縮放特征，我們將所有特征對齊到均值為0，標準差為1。

scaler = StandardScaler()scaler.fit(df)X_scale = scaler.transform(df)df_scale = pd.DataFrame(X_scale, columns=df.columns)df_scale.head()

2. 特征降維

在一些算法如KMeans中，如果數據集的特征維度太大，就很難精確地構建聚類。高維數并不一定意味著成百上千維度的特征。甚至10個維度的特征也會造成準確性問題。

特征降維背后的理論是將原始特征集轉換為更少的人工派生特征，這些特征仍然保留了原始特征中包含的大部分信息。

最流行的特征降維技術之一是主成分分析(PCA)。PCA將原始數據集縮減為指定數量的特征，并將這些特征稱為主成分。我們必須選擇我們希望看到的主成分的數量。我們在我關于KMeans集群的文章中討論了減少特性，我強烈建議您看一看()。

首先，我們需要確定適當的主成分數量。3個主成分似乎占了大約75%的方差。

pca = PCA(n_components=7)pca.fit(df_scale)variance = pca.explained_variance_ratio_ var=np.cumsum(np.round(variance, 3)*100)plt.figure(figsize=(12,6))plt.ylabel('% Variance Explained')plt.xlabel('# of Features')plt.title('PCA Analysis')plt.ylim(0,100.5)plt.plot(var)

現在我們知道了維持一個特定百分比的方差所需的主成分的數量，讓我們對原始數據集應用一個3成分的主成分分析。請注意，第一個主成分占到與原始數據集方差的26%。在本文的其余部分中，我們將使用"pca_df"數據框架。

pca = PCA(n_components=3)pca.fit(df_scale)pca_scale = pca.transform(df_scale)pca_df = pd.DataFrame(pca_scale, columns=['pc1', 'pc2', 'pc3'])print(pca.explained_variance_ratio_)

在3D空間中繪制數據，可以看到DBSCAN存在一些潛在的問題。DBSCAN的一個主要缺點就是它不能準確地對不同密度的數據進行聚類，從下面的圖中，我們可以看到兩個不同密度的單獨集群。在應用DBSCAN算法時，我們可能能夠在數據點較少的聚類結果中找到不錯的聚類方式，但在數據點較多的聚類中的許多數據點可能被歸類為離群值/噪聲。這當然取決于我們對epsilon和最小點值的選擇。

Scene = dict(xaxis = dict(title  = 'PC1'),yaxis = dict(title  = 'PC2'),zaxis = dict(title  = 'PC3'))trace = go.Scatter3d(x=pca_df.iloc[:,0], y=pca_df.iloc[:,1], z=pca_df.iloc[:,2], mode='markers',marker=dict(colorscale='Greys', opacity=0.3, size = 10, ))layout = go.Layout(margin=dict(l=0,r=0),scene = Scene, height = 1000,width = 1000)data = [trace]fig = go.Figure(data = data, layout = layout)fig.show()

3.DBSCAN聚類

方法1

在應用聚類算法之前，我們必須使用前面討論過的"肘形法"來確定合適的epsilon級別。看起來最佳的值在0.2左右。最后，由于我們的數據有3個主成分，我們將把最小點標準設置為6。

plt.figure(figsize=(10,5))nn = NearestNeighbors(n_neighbors=5).fit(pca_df)distances, idx = nn.kneighbors(pca_df)distances = np.sort(distances, axis=0)distances = distances[:,1]plt.plot(distances)plt.show()

將epsilon設置為0.2，將min_samples設置為6，得到了53個集群，影像分數為-0.521，以及超過1500個被認為是離群值/噪聲的數據點。在某些研究領域，53個集群可能被認為是有用的，但我們有一個15000名員工的數據集。從業務的角度來看，我們需要一些可管理的集群(即3-5個)，以便更好地分配工作場所。此外，剪影得分-0.521表明數據點是不正確的聚集。

看看下面的3D圖，我們可以看到一個包含了大多數數據點的集群。出現了一個較小但很重要的聚類簇，但剩下52個聚類簇的規模要小得多。從業務角度來看，這些集群提供的信息不是很多，因為大多數員工只屬于兩個集群。組織希望看到幾個大的集群，以確定它們的有效性，但也能夠從事一些針對集群員工的組織主動性工作(例如。增加培訓、薪酬變化等)。

db = DBSCAN(eps=0.2, min_samples=6).fit(pca_df)labels = db.labels_# Number of clusters in labels, ignoring noise if present.n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)n_noise_ = list(labels).count(-1)print('Estimated number of clusters: %d' % n_clusters_)print('Estimated number of noise points: %d' % n_noise_)print("Silhouette Coefficient: %0.3f" % metrics.silhouette_score(pca_df, labels))

Scene = dict(xaxis = dict(title  = 'PC1'),yaxis = dict(title  = 'PC2'),zaxis = dict(title  = 'PC3'))labels = db.labels_trace = go.Scatter3d(x=pca_df.iloc[:,0], y=pca_df.iloc[:,1], z=pca_df.iloc[:,2], mode='markers',marker=dict(color = labels, colorscale='Viridis', size = 10, line = dict(color = 'gray',width = 5)))layout = go.Layout(scene = Scene, height = 1000,width = 1000)data = [trace]fig = go.Figure(data = data, layout = layout)fig.update_layout(, font=dict(size=12,))fig.show()Image for post

方法2

我們不使用"肘部方法"和最小值啟發式方法，而是使用迭代方法來微調我們的DBSCAN模型。在對數據應用DBSCAN算法時，我們將迭代一系列的epsilon和最小點值。

在我們的例子中，我們將迭代0.5到1.5之間的epsilon值和2-7之間的minPts。for循環將使用這組值運行DBSCAN算法，并為每次迭代生成集群數量和影像分數。請記住，您需要根據數據調整參數。您可能會在一組參數上運行此代碼，并發現產生的最佳影像分數是0.30。為了將更多的點包含到一個集群中，您可能需要增加值。

pca_eps_values = np.arange(0.2,1.5,0.1) pca_min_samples = np.arange(2,5) pca_dbscan_params = list(product(pca_eps_values, pca_min_samples))pca_no_of_clusters = []pca_sil_score = []pca_epsvalues = []pca_min_samp = []for p in pca_dbscan_params:    pca_dbscan_cluster = DBSCAN(eps=p[0], min_samples=p[1]).fit(pca_df)    pca_epsvalues.append(p[0])    pca_min_samp.append(p[1])pca_no_of_clusters.append(len(np.unique(pca_dbscan_cluster.labels_)))    pca_sil_score.append(silhouette_score(pca_df, pca_dbscan_cluster.labels_))pca_eps_min = list(zip(pca_no_of_clusters, pca_sil_score, pca_epsvalues, pca_min_samp))pca_eps_min_df = pd.DataFrame(pca_eps_min, columns=['no_of_clusters', 'silhouette_score', 'epsilon_values', 'minimum_points'])pca_ep_min_df

我們可以看到，通過我們的epsilon和minPts的迭代，我們已經獲得了很大范圍的簇數和影像分數。0.9到1.1之間的epsilon分數開始產生可管理的集群數量。將epsilon增加到1.2或更高會導致集群數量太少，無法在商業上發揮作用。此外，其中一些集群可能只是噪音。我們稍后會講到。

增加的epsilon會減少集群的數量，但每個集群也會開始包含更多的離群點/噪聲數據點，這一點也可以理解為有一定程度的收益遞減。

為了簡單起見，讓我們選擇7個集群并檢查集群分布情況。(epsilon: 1.0和minPts: 4)。

同樣重要的是，運行此代碼串時肯定會遇到的一個常見錯誤。有時，當你設置的參數不合適，for循環最終會變成epsvalues和minsamples的組合，這只會產生一個集群。但是，silhouette ette_score函數至少需要定義兩個集群。您需要限制參數以避免此問題。

在上面的示例中，如果我們將epsilon參數的范圍設置為0.2到2.5，那么很可能會生成一個集群并最終導致錯誤。

你可能會問自己"我們不是應該獲得7個集群嗎?"答案是肯定的，如果我們看一下獨特的標簽/集群，我們看到每個數據點有7個標簽。根據Sklearn文檔，標簽"-1"等同于一個"嘈雜的"數據點，它還沒有被聚集到6個高密度的集群中。我們自然不希望將任何"-1"標簽考慮為一個集群，因此，它們將從計算中刪除。

db = DBSCAN(eps=1.0, min_samples=4).fit(pca_df)labels = db.labels_# Number of clusters in labels, ignoring noise if present.n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)n_noise_ = list(labels).count(-1)print('Estimated number of clusters: %d' % n_clusters_)print('Estimated number of noise points: %d' % n_noise_)print("Silhouette Coefficient: %0.3f" % silhouette_score(pca_df, labels))

set(labels)

從6個DBSCAN派生集群的3D圖中可以看出，盡管密度較小，但位于圖頂端的密度較小的集群對DBSCAN并沒有造成太大影響。如果您還記得的話，DBSCAN很難正確地集群各種密度的數據。頂部的集群和更大的底部集群之間的距離很可能大于1.0的epsilon值。

也就是說，數據集包含額外的高密度集群，但是我們的epsilon和minPts太大了。底部的聚類簇包含至少兩個高密度的聚類簇，然而，由于底部聚類簇的高密度降低了epsilon和minPts，只會產生許多更小的聚類簇。這也是DBSCAN的主要缺點。我一直認為DBSCAN需要第三個參數"min_core"，它將確定一個集群可以被視為有效集群之前的最小核心點數量。

Scene = dict(xaxis = dict(title  = 'PC1'),yaxis = dict(title  = 'PC2'),zaxis = dict(title  = 'PC3'))# model.labels_ is nothing but the predicted clusters i.e y_clusterslabels = db.labels_trace = go.Scatter3d(x=pca_df.iloc[:,0], y=pca_df.iloc[:,1], z=pca_df.iloc[:,2], mode='markers',marker=dict(color = labels, colorscale='Viridis', size = 10, line = dict(color = 'gray',width = 5)))layout = go.Layout(scene = Scene, height = 1000,width = 1000)data = [trace]fig = go.Figure(data = data, layout = layout)fig.update_layout(DBSCAN Clusters (6) Derived from PCA'", font=dict(size=12,))fig.show()

在我們開始之前，讓我們快速了解一下每個集群中的員工數量。似乎cluster 0包含了大部分信息不太豐富的數據點。事實上，如果我們使用0.5的epsilon值和5的minPts運行算法，就會產生63個集群，集群0仍然會包含99%的員工人口。

np.unique(labels, return_counts=True)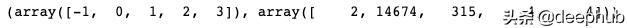

小結

DBSCAN，一種密度聚類算法，常用于非線性或非球面數據集。epsilon和minPts是兩個必需的參數。epsilon是附近數據點的半徑，這些數據點需要被認為是足夠"相似"才能開始聚類。最后，minPts是需要在半徑內的數據點的最小數目。

在我們的示例中，我們試圖根據工作特征對包含15,000名員工的數據集進行聚類。我們首先標準化了數據集以縮放特征。接下來，我們應用主成分分析將維度/特征的數量減少到3個主成分。使用"肘部法"，我們估計了0.2的epsilon值和6的minPts。使用這些參數，我們能夠獲得53個集群，1500個離群值和-0.52的影響分數。不用說，結果并不是很理想。

接下來，我們嘗試了一種迭代的方法來微調epsilon和minPts。我們已經確定了epsilon值為1.0和minPts值為4。該算法返回6個有效的集群(一個-1集群)，只有7個異常值，以及0.46的可觀影像分數。然而，在繪制派生集群時，發現第一個集群包含99%的員工。從業務的角度來看，我們希望我們的集群能夠更加均衡地分布，從而為我們提供關于員工的良好見解。

DBSCAN似乎不是這個特定數據集的最佳聚類算法。

作者：Kamil Mysiak

deephub翻譯組：孟翔杰