Abstract:– Analysis of the visual representations of exponentials.– Proposals to solve current visualization issues.– Call to discussion to come up with a better visual representation convention.

抽象： –分析指數的視覺表示形式。–解決當前可視化問題的建議。–進行討論以提出更好的視覺表示形式慣例。

“The greatest shortcoming of the human race is our inability to understand the exponential function.” — Albert Allen Bartlett, Physics professor

“人類最大的缺點是我們無法理解指數函數。” —物理教授Albert Allen Bartlett

Our big brains brought us the capability to predict the future, and it worked great when our environment was moving on a (rather slow) linear progression, when our ‘food’ moved around the fields from A to B at a constant pace. But many critical aspects of XXI century life move at an exponential rate: human population, computer power, online

我們的大腦使我們有能力預測未來，當我們的環境以(而不是緩慢的)線性發展，當我們的“食物”以恒定的速度從A移到B時，它發揮了很大的作用。 但是，二十一世紀生活的許多關鍵方面都以指數級增長：人口，計算機能力，在線

Graphs and data visualization have been helping understand complex numerical information for centuries with one of the most powerful human tool, an image.

數百年來，圖形和數據可視化一直通過最強大的人工工具之一圖像幫助理解復雜的數字信息。

科學的視覺表示 (Scientific Visual Representations)

Science has two ways to visually represent exponentials: linear & logarithmic.

科學有兩種直觀地表示指數的方式：線性和對數。

Both are accurate, valid and perfectly understandable by people with a scientific background, but it shows some issues when it comes to the mainstream intuition interpretation.

兩者都是準確，有效且具有科學背景的人可以完全理解的，但是當涉及到主流直覺解釋時，這會顯示一些問題。

一直一樣 (All the Same, All The way)

Any section of a linear exponential representation will give you the same trajectory because we tend to escalate the Y axis. The spread of a virus will look similar in a graph of the first 10 days and the first 100 days.

線性指數表示的任何部分都會給您相同的軌跡，因為我們傾向于將Y軸升級。 在前10天和前100天的圖表中，病毒的傳播看起來類似。

走向無限 (Tendency to Infinite)

An exponential curve seems to tend to infinite, but infinite is a rare thing in the real world; actually, most exponential growth or decays are interrupted by some event. It is the lack of a limit reference that makes it feel an endless progression.

指數曲線似乎趨向于無限，但無限在現實世界中是罕見的。 實際上，大多數指數增長或衰變被某個事件中斷。 缺少極限參考使它感到無止境地前進。

缺乏細節 (Lack of details)

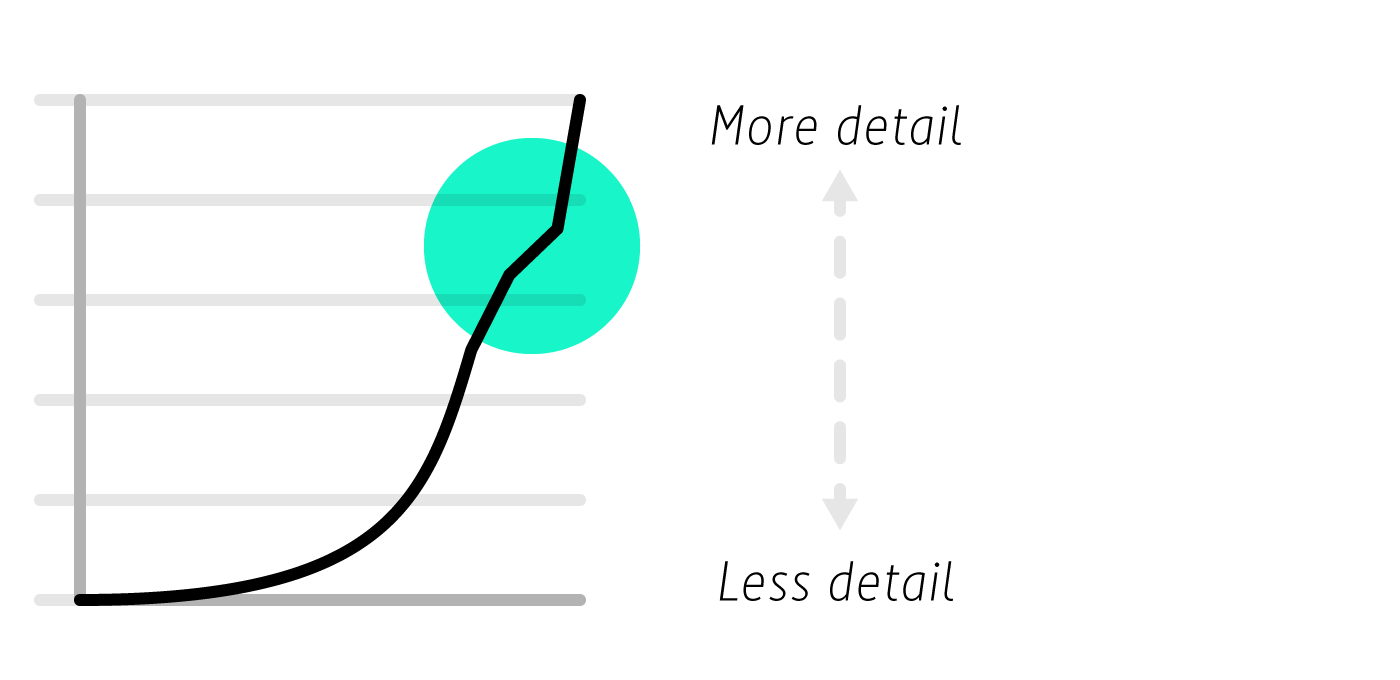
A linear graph will only show more details on the high part of the chart.

線性圖只會在圖表的較高部分顯示更多詳細信息。

A logarithmic graph will only show details on the low part of the chart.

對數圖將僅在圖表的下部顯示詳細信息。

人民指數 (Exponentials for the People)

Human culture is poor in exponential references. The most relevant ones being:

人類文化的指數引用很差。 最相關的是：

Paal Payasam的傳說 (Legend of Paal Payasam)

The Indian Legend of Paal Payasam, in which a reward consisting on doubling the grains of wheat on the squares of a chessboard ends up with an overwhelming amount that surpasses all the amount of wheat grain in the world.

印度傳說中的Paal Payasam ，在其中獲得的獎勵是，在棋盤的正方形上將小麥粒加倍，最終獲得的壓倒性數量超過了世界上所有小麥粒的數量。

十種力量 (Powers of Ten)

The film Powers of Ten by Charles and Ray Eames, which zooms out from our ‘human scale’ exponentially to the scale of the entire universe and then zooms in to the scale of an atom.

查爾斯和雷·伊姆斯 ( Charles and Ray Eames)制作的電影《十大力量》 ，從我們的“人類規模”以指數方式縮小到整個宇宙的規模，然后放大到原子的規模。

更好的視覺方法 (A Better Visual Approach)

To help the lack of natural human skills to understand exponentials it seems relevant to find new ways to visually represent them in a humanly intuitive way.

為了幫助缺乏自然的人類技能來理解指數，尋找新的方式以人類直觀的方式直觀地表示它們似乎很重要。

Nowadays, Infographists develop amazingly creative ways to make abstract data understandable to everyone, but they are mostly individual solutions per each case.

如今，Infographists開發了令人驚訝的創造性方法，使每個人都可以理解抽象數據，但是對于每種情況，它們大多是單獨的解決方案。

It seems necessary to find a visual system relevant for exponentials, accurate and simple enough to be easily implemented and understood.

似乎有必要找到一種與指數相關的視覺系統，其準確度和簡單度應易于實現和理解。

As a Graphic Designer myself, I approached this issue and come up with some early concepts that can help better understand exponentials.

作為一名平面設計師，我親自解決了這個問題，并提出了一些早期概念，可以幫助更好地理解指數。

While there are out there some examples of exponential visualizations showing its progress as an animation or video –the same way Powers of Ten does or like this example of computing exponential growth– I consider that motion generates more complexity in terms of creation and readability, and we miss the simplicity of a single visual impact. So, while I don’t discard a dynamic solution, I prioritize a static image system.

盡管有一些指數化可視化的示例，以動畫或視頻的形式展示了它的進展-就像《十方 冪 》所做的一樣，還是像這個計算指數級增長的示例一樣-我認為運動在創建和可讀性方面會產生更多的復雜性，并且我們錯過了單一視覺沖擊的簡單性。 因此，盡管我不放棄動態解決方案，但仍將靜態圖像系統作為優先級。

分層景觀 (Layered Landscape)

Logarithmic graphs visually remind me of a landscape perspective, where closer objects look bigger and further objects look smaller.

對數圖在視覺上讓我想起了景觀角度，附近的物體看起來更大而其他物體看起來更小。

But in logarithmic graphs there’s a disruptively wrong element that kills the perspective, the line. Imagine the line as a path. If we scale the thickness of the line proportionally to the change of scale it matches our ‘perspective language’ and it makes it more comprehensive.

但是在對數圖中，存在破壞性的錯誤元素，這扼殺了透視線。 想象這條線是一條路徑。 如果我們根據比例尺的變化成比例地縮放線的粗細，則它與我們的“透視語言”相匹配，并且使其更加全面。

Different visual codes would even make it more equal in terms of data details inside the same chart; for example using escalated circles.

不同的視覺代碼甚至可以使同一圖表內的數據細節更加平等； 例如使用升級的圈子。

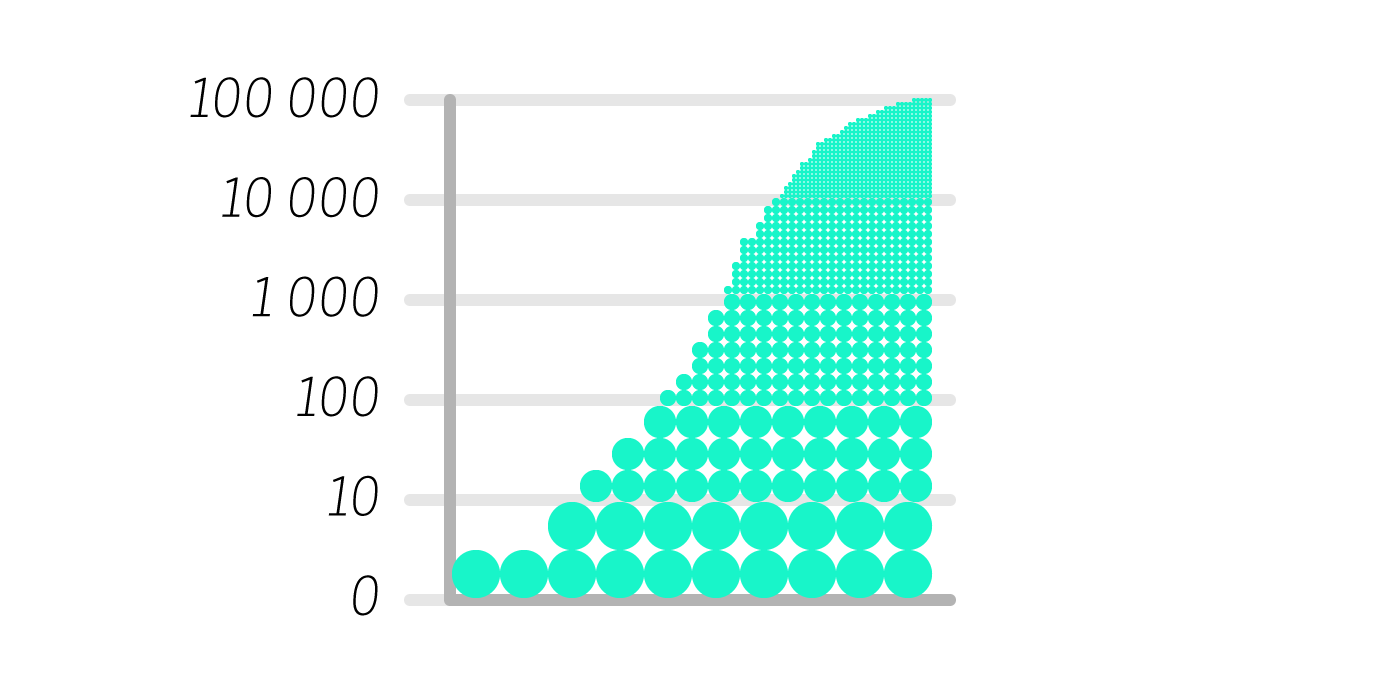
有限參考 (Finite Reference)

As mentioned before, despite the impression of a curve to the infinite, exponentials have limits and representing this reality (as far as possible) would help understand where is this curve going.

如前所述，盡管給人以無限曲線的印象，但指數是有極限的，并且(盡可能)表示這一現實將有助于理解該曲線的去向。

While a context reference is sometimes used in a graph explanation or in the graph itself, the suggestion is to close down the graph itself where the trajectory seems to continue to infinite.

雖然有時在圖形說明中或圖形本身中使用上下文引用，但建議是在軌跡似乎繼續無限的地方關閉圖形本身。

工作正在進行中 (Work in Progress)

Those are very simple approximations to solve the issues above mentioned, not except of issues themselves. I’m personally invested in the topic and will try to learn more about it and find better solutions.

這些是解決上述問題的非常簡單的近似方法，除了問題本身。 我對這個主題進行了個人投資，并將嘗試進一步了解該主題并找到更好的解決方案。

討論電話 (A Call to Discussion)

I write this article from a designer perspective and with no scientific background, my purpose is to open a debate for science and design to reach a convention that feels natural for everyone to understand. My approaches are just a kick-start and I’d like to hear the thoughts of other creative brains –either scientific or designer.

我是從設計者的角度寫這篇文章的，沒有科學背景，我的目的是為科學和設計展開一場辯論，以達成讓每個人都理解的慣例。 我的方法只是一個開端，我想聽聽其他有創造力的大腦(無論是科學專家還是設計師)的想法。

I encourage others to explore the topic and I propose the hashtag #VisualizingExponentials (any platform) to follow up on other comments and approaches. I’ll look at putting together a compilation in short time. I’m thrilled to see where this can go.

我鼓勵其他人探索該主題，并建議使用#VisualizingExponentials (任何平臺)標簽，以跟進其他評論和方法。 我將在很短的時間內整理一下匯編。 我很高興看到這可以去哪里。

Related Links

相關鏈接

Visual explanation of exponentials: https://setosa.io/ev/exponentiation/ by Victor Powell

：指數的視覺解釋 https://setosa.io/ev/exponentiation/ 由 維克多·鮑威爾

An approach to exponential bias applied to SARS-CoV-2 spread case https://towardsdatascience.com/dealing-with-our-systematic-misjudgment-of-covid-19-exponential-growth-3d367c9546d9 by Yannis Kopsinis

Yannis Kopsinis的 SARS-CoV-2傳播案例的指數偏倚方法 https://towardsdatascience.com/dealing-with-our-systematic-misjudgment-of-covid-19-exponential-growth-3d367c9546d9