一個比線段樹代碼還要又臭又長的數據結構,各式各樣的函數,咱也不知道別人怎么記住的,咱也不敢問
SPLAY的性質
1.某個節點的左子樹全部小于此節點,右子樹全部大于此節點
2.中序遍歷splay輸出的序列是按從小到大的順序
(我當時忽略了性質2,以為大小關系只存在于單獨的左右兒子和父節點,后來問了同學才知道,我沒看過二叉排序樹,我能怎么辦)
詢問左右兒子
就是查詢一下x是fa的左兒子還是右兒子
int get(int x) {return a[a[x].fu].son[1]==x; }
?
更新數據
由于每次翻轉之后左右兒子的信息都會改變,所以需要更新一下size
void gx(int x) {a[x].size=a[a[x].son[0]].size+a[a[x].son[1]].size+a[x].js; }
?
上旋
什么是上旋呢,簡單來說就是兒子想當爹,然后他還成功了,也不知道這個爹會不會被氣死,就是把自己父節點變成自己的一個兒子,但是對于一個有兩個子節點的子節點,顯然父節點沒地方去,又因為需要保證平衡樹的性質(左子樹小于父節點小于右子樹),所以肯定子節點的某一個葉節點要去給父節點當兒子,根據splay性質中的大小關系,如果子節點是父節點的左兒子那父節點就要去當子節點的右兒子,此時根據splay的性質直接讓子節點的右兒子去當父節點的左兒子即可,這樣就完成了一次翻轉并且沒有改變splay的性質,若子節點是父節點的右兒子,同理交換兒子,總結一下就是假設右旋x,x是fa的0兒子就讓x的1兒子去當fa的0兒子,fa變成x的1兒子(0和1就是一個左一個右)
void sx(int x) {int f=a[x].fu,ff=a[f].fu;int z1=get(x),z2=get(f);a[f].son[z1]=a[x].son[z1^1]; a[a[x].son[z1^1]].fu=f;a[x].son[z1^1]=f; a[f].fu=x;a[ff].son[z2]=x; a[x].fu=ff;gx(f); gx(x); }
?
雙旋
我覺得雙旋就是上旋中的一種特殊情況,就是子節點,父節點,祖父節點在同一條線上,這時需要先上旋父節點(據說直接上旋慢,不夠優秀,而且雙旋好像還可以減小期望深度,我并沒有模擬),同一條線的話,特判一下就可以了,記得更新根節點
void splay(int x,int mb) {while(a[x].fu!=mb){int f=a[x].fu,ff=a[f].fu;int z1=get(x),z2=get(f);if(ff!=mb){if(z1==z2) sx(f);else sx(x);}sx(x);}if(mb==0) root=x; }
?
幾個基本操作
1.插入節點
插入的話,我覺得和權值線段樹那種遞歸的原理差不多,遍歷來找到合適的位置,加入已經有這個點就直接cnt++,如果沒有的話就新建一個節點,新建之后的話把新建的點旋到根維護下樹就可以了
void cr(int x) {int dq=root,f=0;while(a[dq].w!=x&&dq!=0){f=dq;dq=a[dq].son[a[dq].w<x];}if(dq!=0) {a[dq].js++; gx(dq);}else{dq=++num;if(f!=0) a[f].son[a[f].w<x]=dq;a[dq].size=1; a[dq].js=1;a[dq].fu=f; a[dq].w=x;}splay(dq,0); }
?
2.刪除結點
刪除還是和插入一樣,有兩種情況,如果這個節點的個數不為一直接cnt--,然后旋到根,如果為一的話刪除這個點又不能影響其他點,但是你沒辦法保證刪除的每一個點都沒有葉子節點,這個時候就需要上旋來保證刪除的點沒有葉子結點,具體操作就是把前驅旋到根,后繼旋到前驅下面,這樣的話被刪除的點就變成了葉子節點,直接清零刪除就可以了
void sc(int x) {int qqq=qq(x),hjh=hj(x);splay(qqq,0); splay(hjh,qqq);int z=a[hjh].son[0];if(a[z].js>1) {a[z].js--; gx(z); splay(z,0);}else a[hjh].son[0]=0; }
?
3.查詢某值排名
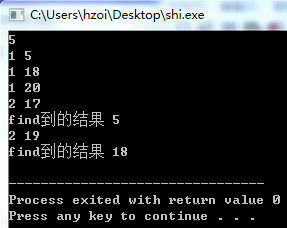
查詢排名先要找到這個值在樹中的位置,當然如果沒有這個值的話會一直找的葉子節點(也不一定是最接近查詢值的點,我運行了一下,發現他會找到第一個比這個值小的值,而不是最接近這個數的值),這種操作的話可以搜極大值和極小值來找到樹中最大值和最小值,找到這個值之后就簡單了,把這個值上旋到根的位置,他左邊都是比他小的,右邊都是比他大的,那么他左子樹的size+1就是這個值的排名
int find(int x) {int dq=root;while(a[dq].w!=x&&a[dq].son[a[dq].w<x]!=0)dq=a[dq].son[a[dq].w<x];return dq; } int cpm(int x) {splay(find(x),0);return a[a[root].son[0]].size; }
?
關于find函數的運行結果(1為插入2為find查詢)
4.查詢某值的前驅/后繼
x的前驅:小于x的最大的數 ???x的后繼:大于x的最小的數
用find函數查找x,把x上旋到根的位置,由于x可能不存在,而find查到的又是第一個比他小的值,所以有可能上旋后根節點就是要查詢的前驅,所以要特判,但是根據我的運行結果來說,我認為后繼不需要特判,如果怕不保險,特判也無所謂,反正特判應該是肯定對的那個,如果有x這個值那么前驅就是他的左子樹的最右葉子節點,同理,后繼就是他右子樹的最左葉子節點,一直向下搜就可以了
int qq(int x) {splay(find(x),0);int dq=root;if(a[dq].w<x) return dq;dq=a[dq].son[0];while(a[dq].son[1]!=0) dq=a[dq].son[1];return dq; } int hj(int x) {splay(find(x),0);int dq=root;if(a[dq].w>x) return dq;dq=a[dq].son[1];while(a[dq].son[0]!=0) dq=a[dq].son[0];return dq; }
?
5.查詢第k小值
跟主席樹求第k小有點相似,通過記錄左右子樹包含的元素個數與k進行比較,選擇暴力遞歸左兒子或者右兒子,如果當前節點的左子樹元素個數小于k,那么第k小就在右子樹中,k減去左子樹元素個數+當前點的cnt值(還有這個元素自己)后暴力搜索右子樹,如果左子樹元素個數大于k,直接搜索左子樹,假如k介于左子樹右子樹的size之間(一定要想清為什么有范圍,因為同一個值可能出現多次,導致他自己代表的值就不唯一,我死在這好久),那么當前點就是第k小
int csz(int x) {int dq=root;while(1){int ls=a[dq].son[0];if(a[ls].size>=x) dq=ls;else if(a[ls].size+a[dq].js<x){x-=a[ls].size+a[dq].js;dq=a[dq].son[1];}else return a[dq].w;} }
?
到此,普通平衡樹就可以搞定了
關于插入結點那一塊,雖然最后的splay執行中會更新結點,但是我還是覺得在直接更新cnt之后更新一下節點信息比較好
現在思路是理出來了,也不知道代碼能不能打下來(我依舊是個蒟蒻)
第一次完整的整理了一個知識點還有點興奮




)


精)








高級職位)


