CCF201409-5 拼圖（30分）

試題編號：	201409-5
試題名稱：	拼圖
時間限制：	3.0s
內存限制：	256.0MB
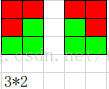
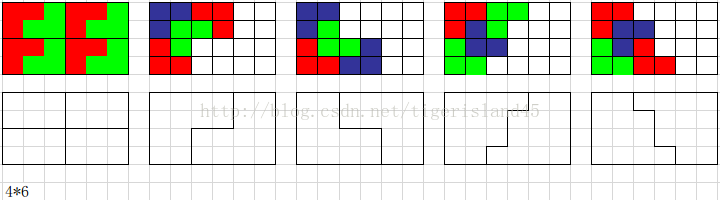
問題描述：	問題描述 給出一個n×m的方格圖，現在要用如下L型的積木拼到這個圖中，使得方格圖正好被拼滿，請問總共有多少種拼法。其中，方格圖的每一個方格正好能放積木中的一塊。積木可以任意旋轉。 輸入格式 輸入的第一行包含兩個整數n, m，表示方格圖的大小。 輸出格式 輸出一行，表示可以放的方案數，由于方案數可能很多，所以請輸出方案數除以1,000,000,007的余數。 樣例輸入 6 2 樣例輸出 4 樣例說明 四種拼法如下圖所示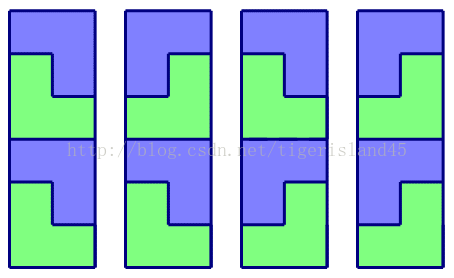： 評測用例規模與約定 在評測時將使用10個評測用例對你的程序進行評測。 　　評測用例1和2滿足：1<=n<=30，m=2。 　　評測用例3和4滿足：1<=n, m<=6。 　　評測用例5滿足：1<=n<=100，1<=m<=6。 　　評測用例6和7滿足：1<=n<=1000，1<=m<=6。 　　評測用例8、9和10滿足：1<=n<=10^15，1<=m<=7。

問題鏈接：CCF201409試題。

問題描述：（參見上文）。

問題分析：也許從數學上先推演一下比較好，這有點難。

看似可以用遞歸函數來實現，實際做起來沒有那么容易。只得了30分，有勝于無而已。

對于輸入的n和m，若n*m不是3的倍數，則肯定無法完全覆蓋。同時，如果不是6的倍數則不能完全覆蓋。

n和m哪個更大是不知道的，假設n<=m的情況下進行計算即可，若n>m將n和m交換即可。題意中則相反，是m<=n，實際上是一樣的。

以下給出若各種拼圖組合，可以在其基礎上找出遞歸函數關系：

　

　　

　

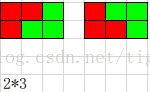
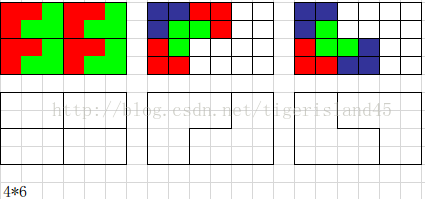
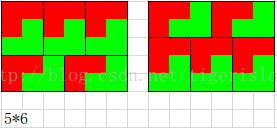
程序說明：程序有待改進，或者需要新的思路。

提交后得30分的C++語言程序如下：

/* CCF201409-5 拼圖 */#include <iostream>using namespace std;const long long MOD = 1000000007;// 模冪計算函數
inline long long powermod(int x, int y, long long mod)
{long long ans = 1;while(y) {if(y & 1) {ans *= x;ans %= mod;}x *= x;x %= mod;y >>= 1;}return ans;
}long long puzzle(int n, int m)
{long long b1, b2;if(n <= 1 || m <= 1)return 0;// 面積不是3的倍數則不可能if((n * m) % 3 != 0)return 0;// 讓n<=mif(n > m) {int temp = n;n = m;m = temp;}if(n == 2) {   // 2 * 3 * k, k = m / 3// n=2時，m必須是3的倍數if(m % 3 != 0)return 0;return powermod(2, m / 3, MOD);} else if(n == 3) { // 3 * 2 * k, k = m / 2// n=3時，m必須是2的倍數if(m % 2 != 0)return 0;return powermod(2, m / 2, MOD);} else if(n == 4 && m == 6) { // 4 * 6b1 = puzzle(2, m);  // 分為兩半b2 = puzzle(2, 3);   // 4*6異形數量return (b1 * b1 + b2) % MOD;} else if(n == 4) { // 4 * 3 * 2 * k, k = m / 6 或　4 * 3 * 2 * k + 4 * 3, k = m / 6b1 = powermod(puzzle(4, 6), m / 6, MOD);if(m % 6 == 0) {return b1;} else if(m % 6 == 3) {// 除了組合，還需要考慮排列b2 = puzzle(3, 4);return b1 * b2 * (m / 6 + 1) % MOD;} elsereturn 0;} else if(n == 5 && m == 6) {long long b1, b2;b1 = puzzle(3, m);b2 = puzzle(2, m);return b1 * b2 * 2 % MOD;   // 64} else if(n == 5) {if(m % 6 != 0)return 0;return powermod(puzzle(5, 6), m / 6, MOD);} else if(n == 6 && m == 6) {// 上下分，左右分，４＊６異形與２＊６拼接，６＊６異形（２種）b1 = puzzle(3, m);  // 上下分，或左右分b2 = puzzle(2, 3);   // 4*6異形數量return (b1 * b2 * 2 + b2 * puzzle(2, 6) * 4 + 2) % MOD;} else if(n == 6) {// ６＊６不正確，這個計算就沒有意義了return 0;} else {// 其他情況：不考慮return 0;}
}int main()
{int n, m;long long ans;cin >> n >> m;ans = puzzle(n, m);cout << ans << endl;return 0;
}

改進：上述程序提交后只得30分，所以進行了進一步的分析與改進：

1.使得方格圖正好被拼滿，需要m*n是6的倍數，因為積木塊面積為3。程序中35-37行代碼改為：

    // 方格圖被完全拼滿，面積不是6的倍數則不可能if((n * m) % 6 != 0)return 0;

2.根據題意，m最大為7，即只需要考慮m=2,3,4,5,6,7的情況。這也是得100分的希望所在。

所以，程序中只需要考慮n=2,3,4,5,6,7的情況（程序中，與題意相比，n和m互換）。

3.程序中增加n=7的代碼，需要考慮6*7和7*m的情況。對于6*7的方格圖，可以由6*2和6*5的方格圖組成，也可以由6*3和6*4的方格圖組成。

改進后提交得30分的C++語言程序如下：

/* CCF201409-5 拼圖 */#include <iostream>using namespace std;const long long MOD = 1000000007;// 模冪計算函數
inline long long powermod(int x, int y, long long mod)
{long long ans = 1;while(y) {if(y & 1) {ans *= x;ans %= mod;}x *= x;x %= mod;y >>= 1;}return ans;
}long long puzzle(int n, int m)
{long long b1, b2;if(n <= 1 || m <= 1)return 0;// 方格圖被完全拼滿，面積不是6的倍數則不可能if((n * m) % 6 != 0)return 0;// 讓n<=mif(n > m) {int temp = n;n = m;m = temp;}if(n == 2) {   // 2 * 3 * k, k = m / 3// n=2時，m必須是3的倍數if(m % 3 != 0)return 0;return powermod(2, m / 3, MOD);} else if(n == 3) { // 3 * 2 * k, k = m / 2// n=3時，m必須是2的倍數if(m % 2 != 0)return 0;return powermod(2, m / 2, MOD);} else if(n == 4 && m == 6) { // 4 * 6b1 = puzzle(2, m);  // 分為兩半b2 = puzzle(2, 3);   // 4*6異形數量return (b1 * b1 + b2) % MOD;} else if(n == 4) { // 4 * 3 * 2 * k, k = m / 6 或　4 * 3 * 2 * k + 4 * 3, k = m / 6b1 = powermod(puzzle(4, 6), m / 6, MOD);if(m % 6 == 0) {return b1;} else if(m % 6 == 3) {// 除了組合，還需要考慮排列b2 = puzzle(3, 4);return b1 * b2 * (m / 6 + 1) % MOD;} elsereturn 0;} else if(n == 5 && m == 6) {long long b1, b2;b1 = puzzle(3, m);b2 = puzzle(2, m);return b1 * b2 * 2 % MOD;   // 64} else if(n == 5) {if(m % 6 != 0)return 0;return powermod(puzzle(5, 6), m / 6, MOD);} else if(n == 6 && m == 6) {// 上下分，左右分，４＊６異形與２＊６拼接，６＊６異形（２種）b1 = puzzle(3, m);  // 上下分，或左右分b2 = puzzle(2, 3);   // 4*6異形數量return (b1 * b2 * 2 + b2 * puzzle(2, 6) * 4 + 2) % MOD;} else if(n == 6 && m == 7) {b1 = puzzle(2, 6) * puzzle(5, 6);b2 = puzzle(3, 6) * puzzle(4, 6);return (b1 + b2) % MOD;} else if(n == 6) {// ６＊６不正確，這個計算就沒有意義了return 0;} else if(n == 7) {return powermod(puzzle(6, 7), m / 6, MOD);} else {// 其他情況：不考慮return 0;}
}int main()
{int n, m;long long ans;cin >> n >> m;ans = puzzle(n, m);cout << ans << endl;return 0;
}

經過改進的程序仍然的30分，增加的有關7*m的代碼完全不得分。

由于6*7的方格圖，可以由6*2和6*5的方格圖組成，也可以由6*3和6*4的方格圖組成，那應該是以下幾種方格圖的組合數計算有錯誤：

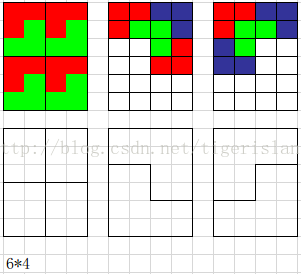
6*2

6*5

6*3

6*4

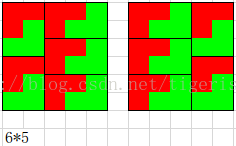
經過仔細考察和梳理，終于發現4*6至少漏算了一個情況，至少應該如下圖所示：

上述程序的56-50行改為（異形數量*2）：

    } else if(n == 4 && m == 6) { // 4 * 6b1 = puzzle(2, m);      // 分為兩半b2 = puzzle(2, 3) * 2;   // 4*6異形數量return (b1 * b1 + b2) % MOD;

改進后提交只得20分，分數更少了，懷疑測試數據有BUG。

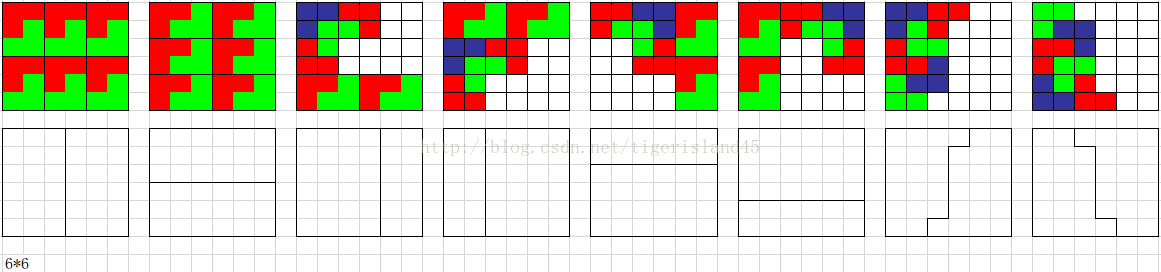
下一步只能考慮先改進6*6的情形了。