本節書摘來自異步社區《MATLAB信號處理超級學習手冊》一書中的第2章，第2.5節，作者：MATLAB技術聯盟 , 史潔玉著，更多章節內容可以訪問云棲社區“異步社區”公眾號查看

2.5 離散時間信號中的運算

MATLAB信號處理超級學習手冊

2.5.1 離散時間系統響應

離散時間LTI系統可用線性常系數差分方程來描述，即：

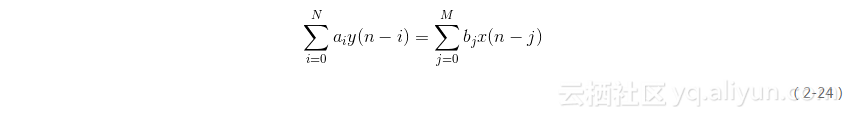
其中，a i(i=0,1,…,N)和b j(j=0,1,…,M)為實常數

MATLAB中函數filter可對式(2-24)的差分方程在指定時間范圍內的輸入序列所產生的響應進行求解。函數filter的語句格式為

y=filter(b,a,x)

其中，x為輸入的離散序列；y為輸出的離散序列，y的長度與x的長度一樣；b與a分別為差分方程右端與左端的系數向量。

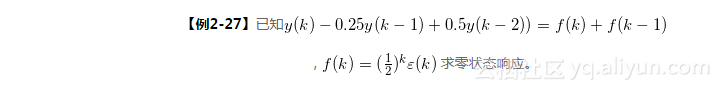
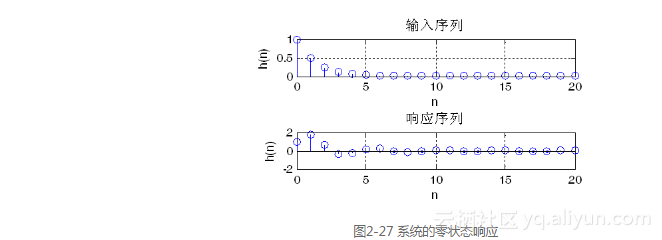
運行程序如下：

a=[1 -0.25 0.5];

b=[1 1];

t=0:20;

x=(1/2).^t;

y=filter(b,a,x)

subplot(2,1,1)

stem(t,x)

title('輸入序列')

grid on

xlabel('n'); ylabel('h(n)');

subplot(2,1,2)

stem(t,y)

xlabel('n'); ylabel('h(n)');

title('響應序列')

grid on

運行結果如圖2-27所示。

2.5.2 離散時間系統的沖激響應和階躍響應

在MATLAB中，求解離散時間系統單位沖激響應，可應用信號處理工具箱提供的函數impz，其調用形式為：

h=impz(b, a, k)

式中，a,b分別是差分方程左、右端的系數向量，k表示輸出序列的取值范圍(可省略)，h就是系統單位沖激響應(如果沒有輸出參數，直接調用impz(b, a, k)，則MATLAB將會在當前繪圖窗口中自動畫出系統單位沖激響應的圖形)。

對于MATLAB 6.x及以上版本，在信號處理工具箱中還提供了求解離散時間系統單位階躍響應的函數stepz，其調用形式為：

h=stepz(b,a,k)

式中參數與impz函數相同，如果沒有輸出參數，直接調用stepz(b,a,k)，則MATLAB將會在當前繪圖窗口中自動畫出系統單位階躍響應的圖形。

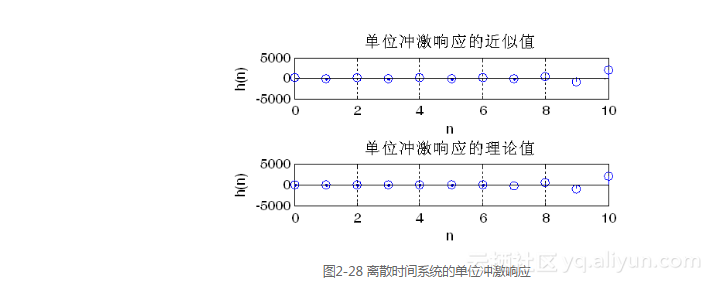
【例2-28】用impz函數求下列離散時間系統的單位沖激響應，并與理論值進行比較：

y(k)+3y(k-1)+2y(k-2)=f(k)。

運行程序如下：

k=0:10;

a=[1 3 2];

b=[1];

h=impz(b,a,k);

subplot(2,1,1);stem(k,h);

xlabel('n'); ylabel('h(n)');

title('單位沖激響應的近似值');

grid on;

hk=-(-1).^k+2*(-2).^k;

subplot(2,1,2);stem(k,h);

xlabel('n'); ylabel('h(n)');

title('單位沖激響應的理論值');

grid on;

運行結果如圖2-28所示。

2.5.3 離散時間信號的卷積和運算

卷積是用來計算系統零狀態響應的有力工具。例如：對于連續時間系統，有y(t)=x(t)h(t),其中h(t)為系統傳遞函數(即沖激響應)；對于離散時間系統，有y(n)=x(n)h(n)，其中h(n)為系統傳遞函數(即單位沖激響應)。

由于系統的零狀態響應是激勵與系統的單位取樣響應的卷積，因此卷積運算在離散時間信號處理領域被廣泛應用。離散時間信號的卷積定義為：

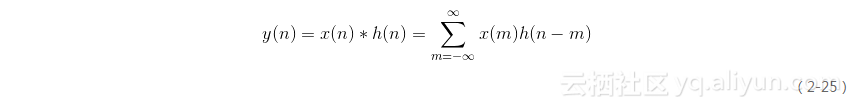
可見，離散時間信號的卷積運算是求和運算，因而常稱為“卷積和”。

MATLAB信號處理工具箱提供了一個計算兩個離散序列卷積和的函數，其調用形式為：

c=conv(a,b)

式中，a、b分別為待卷積的兩序列的向量表示，c是卷積結果。向量c的長度為向量a、b的長度之和減1，即length(c)=length(a)+length(b)1。事實上，研究conv.m函數的源代碼可知，conv函數其實就是利用前面介紹過的函數來實現的。

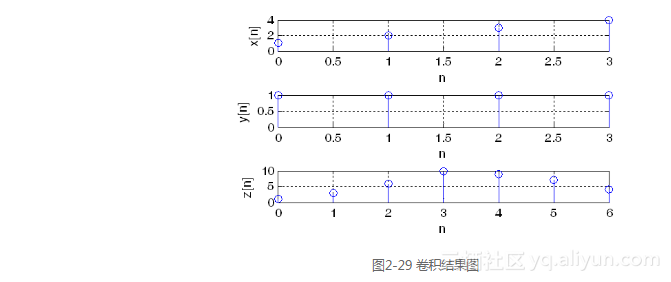
【例2-29】已知序列x[n]={1,2,3,4;n=0,1,2,3},y[n]={1,1,1,1;n=0,1,2,3,4};利用MATLAB計算x[n]*y[n]并畫出卷積結果。

運行程序如下：

x=[1,2,3,4];

y=[1,1,1,1];

z=conv(x,y)

subplot(3,1,1);

stem(0:length(x)-1,x);

ylabel('x[n]'); xlabel('n');

grid on

subplot(3,1,2);

stem(0:length(y)-1,y);

ylabel('y[n]'); xlabel('n');

grid on

subplot(3,1,3);

stem(0:length(z)-1,z);

ylabel('z[n]'); xlabel('n');

grid on

運行結果如下：

z =

1 3 6 10 9 7 4

運行結果如圖2-29所示。

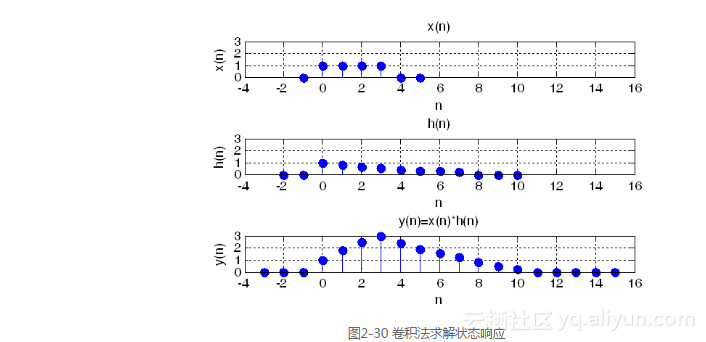
【例2-30】已知某系統的單位取樣響應為hleft( n right) = 0.8^n left[ {uleft( n right) - uleft( {n - 8} right)} right] ，試用MATLAB求當激勵信號為x(n) = u(n) - u(n - 4) 時，系統的零狀態響應。

運行程序如下：

clear

nx=-1:5;

nh=-2:10;

x=uDT(nx)-uDT(nx-4);

h=0.8.^nh.*(uDT(nh)-uDT(nh-8));

y=conv(x,h);

ny1=nx(1)+nh(1);

ny=ny1+(0:(length(nx)+length(nh)-2));

subplot(311)

stem(nx,x,'fill'),grid on

xlabel('n'),ylabel('x(n)');

title('x(n)')

axis([-4 16 0 3])

subplot(312)

stem(nh,h','fill'),grid on

xlabel('n');ylabel('h(n)');

title('h(n)')

axis([-4 16 0 3])

subplot(313)

stem(ny,y,'fill'),grid on

xlabel('n');ylabel('y(n)');

title('y(n)=x(n)*h(n)')

axis([-4 16 0 3])

運行結果如圖2-30所示。

程序中產生單位階躍子程序如下：

function y=uDT(n)

y=n>=0;

%當參數為非負時輸出1