通常我們求解一維卷積或者二維卷積都是采用模板平移的方法，今天我們介紹一種新的求解方法，可以一次性求出所有的結果。

一維卷積

卷積定義

對于兩個長度分別為m和n的序列x(i)和g(i)有，

$$h(i)=x(i)*g(i)=\sum_{j}x(j)g(i-j)$$
上式給出了長度為N=m+n-1的輸出序列。稱為一維情況下的卷積公式。

循環矩陣

參考百度百科：
在線性代數中，循環矩陣是一種特殊形式的 Toeplitz矩陣，它的行向量的每個元素都是前一個行向量各元素依次右移一個位置得到的結果。由于可以用離散傅立葉變換快速解循環矩陣，所以在數值分析中有重要的應用。

定義

形式為

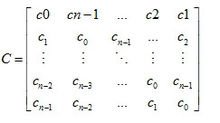
的 矩陣 C 就是循環矩陣。

性質

循環矩陣的性質：
1. 循環矩陣遵循代數運算法則。對于兩個循環矩陣 A 與 B 來說，A + B 也是循環矩陣。AB 也是循環矩陣，并且 AB=BA。
2. 循環矩陣的特征向量矩陣是同樣維數的離散傅立葉變換矩陣，因此循環矩陣的特征值可以很容易地通過快速傅立葉變換計算出來。

循環矩陣求解卷積

按照定義，卷積后的序列長為N=m+n-1;
于是分別用0擴充序列x,g，分別為：

$$x_p(i)=\left\{\begin{matrix} x(i) & 1\leqslant x \leqslant m\\ 0& m<i\leqslant N \end{matrix}\right.$$
$$g_p(i)=\left\{\begin{matrix} g(i) & 1\leqslant x \leqslant n\\ 0&n<i\leqslant N \end{matrix}\right.$$
由于是用g去卷積f,所以構造g的循環矩陣：
$$G=\begin{bmatrix} g_p(1) &g_p(N) &g_p(N-1) &\cdots & g_p(2) \\ g_p(2) &g_p(1) &g_p(2) &\cdots &g_p(3) \\ \vdots & \vdots & \vdots &\ddots &\vdots \\ g_p(N) &g_p(N-1)&g_p(N-2) &\ddots & g_p(1) \end{bmatrix}$$
則 $$h=G\cdot x_p=\begin{bmatrix} g_p(1) &g_p(N) &g_p(N-1) &\cdots & g_p(2) \\ g_p(2) &g_p(1) &g_p(2) &\cdots &g_p(3) \\ \vdots & \vdots & \vdots &\ddots &\vdots \\ g_p(N) &g_p(N-1)&g_p(N-2) &\ddots & g_p(1) \end{bmatrix}\begin{bmatrix} x_p(1)\\ x_p(2)\\ \vdots \\ x_p(N) \end{bmatrix}$$
則h就是卷積后的向量。

二維卷積

卷積定義

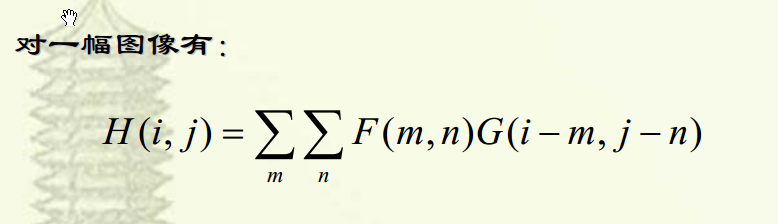
循環矩陣求解方法

舉例

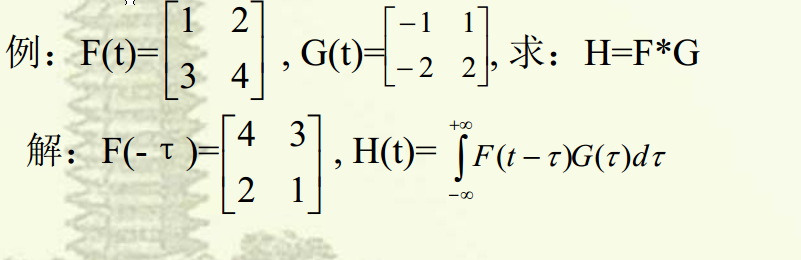
參考文獻

1. 北大高級遙感數字圖像處理（碩士生課程）
2. 離散卷積與自相關