問題

給定離散點集$X_i=(x_i,y_i),i=1,2,...N$，我們希望找到誤差最小的橢圓去擬合這些離散點。

方法

由于橢圓的形式可以給定， 自然我們將使用最小二乘法來求解橢圓。主要依據論文《Direct least squares fitting of ellipsees, Fitzgibbon, Pilu and Fischer in Fitzgibbon, A.W., Pilu, M., and Fischer R.B.,Proc. of the 13th Internation Conference on Pattern Recognition, pp 253–257, Vienna, 1996》。

橢圓擬合的難點

通常我們使用最小二乘法求解如下的最優化問題：

$$Min\sum _{i=1}^{N}f(x_i,E)$$
這里$f(x_i,E)$表示點$x_i$到E（指待擬合的橢圓）的最小距離。一般稱為幾何距離。但是我們很難直接給定幾何距離的解析表達，因此很難求出。因此我們退而求其次，我們采用：為橢圓寫下隱式方程，然后將點的坐標帶入此隱式方程就得到了點到橢圓的距離。這種方法對于直線擬合、圓擬合，返回的就是到其的真實距離。而對于橢圓擬合，它返回的值是與距離有類似的屬性，但不是一個真正的距離值。因此這個距離被稱為代數距離。
橢圓可以用下面的隱式方程表達：

$$a_1{x}^2+a_{2}xy+a_3{y}^2+a_{4}x+a_{5}y+a_6=0$$

與直線類似（直線表達為：$a_{1}x+a_{2}y+a_3=0$）,上式的一組參數也是齊次量，即只能定義到一個比例因子。而且表達式也能表達雙曲線和拋物線。而橢圓
通常要求:$a_2^2?4a_1{a}_4<0$。最好通過令$a_2^2?4a_1{a}_4=?1$,即可同時解決這兩個問題。

請參考維基百科橢圓定義和wolfram MathWorld 橢圓定義

一般的求解過程

對上面的橢圓方程改寫為：

$$f(a,(x,y))=D?a=0$$

這里$D=(x^2,xy,y^2,x,y,1)$,$a=(a_1,a_2,a_3,a_4,a_5,a_6)$.
于是給定N個離散點$X_i=(x_i,y_i),i=1...N$,通過最小化代數距離：

$$Min\Delta (a,X)=\sum _{i=1}^N(f(a,X_i){)}^2$$

重寫上式，即有：

$$Min\Delta (a,X)=\sum _{i=1}^N{a}^T{D}_i^T{D}_{i}a=a^{T}Sa$$

這里$S=\sum D_i^T{D}_i$為6x6矩陣。
另外，我們可以把各個$D_i$合并起來，則有
$$\hat{D}=?\begin{array}{c}{D}_1\\ D_2\\ ?\\ D_N\end{array}?$$
因此：
$$S={\hat{D}}^T\hat{D}$$

此外，我們還有約束條件：
$a_2^2?4a_1{a}_4<0$，可以改寫為：

$$a^{T}Ca=?1$$

其中$C\in R^{6\times 6}$,且大部分為0，只有$C_{1,3}=C_{3,1}=?2,C_{2,2}=1$。
因此綜合上來即為，求解如下的最優化問題：

$$Min{a}^{T}Sa$$
$$s.t.a^{T}Ca=?1$$

公式和拉格朗日乘子法

通過使用拉格朗日乘子法 ，我們可以得到

$$L(a)=a^{T}Sa?\lambda (a^{T}Ca+1)$$

然后求解${?}_{a}L(a)=0$可以求解得到：
$$Sa=\lambda Ca$$

上式是經典的廣義特征值問題。我們可以直接求解，其中$\lambda$為廣義特征值，而a為廣義特征向量
論文 中指出有且僅有一個負的特征值，且其對應的特征向量即為我們需要的橢圓方程的系數，即這里的a.

一般的圓錐方程到標準橢圓方程的轉化。

當我們求解得到了圓錐曲線的系數，即a,我們一般需要獲得橢圓的標準方程，也就是獲得橢圓的如下參數：
中心$(c_x,c_y)$、長短半軸$r_1,r_2$,旋轉角度$\theta$.

這里我們可以給出結果，也可以自己結合橢圓的標準形式與圓錐曲線的方程去推導.

參考文獻：http://mathworld.wolfram.com/Ellipse.html.
##編程實現
下面描述matlab與c++實現。

matlab

% fitellip gives the 6 parameter vector of the algebraic circle fit
% to a(1)x^2 + a(2)xy + a(3)y^2 + a(4)x + a(5)y + a(6) = 0
% X & Y are lists of point coordinates and must be column vectors.(或者行向量)
function a = fitellip(X,Y)% normalize datamx = mean(X);my = mean(Y);sx = (max(X)-min(X))/2;sy = (max(Y)-min(Y))/2;x = (X-mx)/sx;y = (Y-my)/sy;% Force to column vectorsx = x(:);y = y(:);% Build design matrixD = [ x.*x  x.*y  y.*y  x  y  ones(size(x)) ];% Build scatter matrixS = D'*D;% Build 6x6 constraint matrixC(6,6) = 0; C(1,3) = -2; C(2,2) = 1; C(3,1) = -2;% Solve eigensystem[gevec, geval] = eig(S,C);% Find the negative eigenvalue[NegR, NegC] = find(geval < 0 & ~isinf(geval));% Extract eigenvector corresponding to positive eigenvalueA = gevec(:,NegC);% unnormalizea = [A(1)*sy*sy,   ...A(2)*sx*sy,   ...A(3)*sx*sx,   ...-2*A(1)*sy*sy*mx - A(2)*sx*sy*my + A(4)*sx*sy*sy,   ...-A(2)*sx*sy*mx - 2*A(3)*sx*sx*my + A(5)*sx*sx*sy,   ...A(1)*sy*sy*mx*mx + A(2)*sx*sy*mx*my + A(3)*sx*sx*my*my   ...- A(4)*sx*sy*sy*mx - A(5)*sx*sx*sy*my   ...+ A(6)*sx*sx*sy*sy   ...]';

c++

我們參考了網上的版本，并修復了他的問題，最終也做出了和matlab一樣的效果。其中最關鍵的是廣義特征值的求解。我們使用了Eigen與clapack庫。其中Eigen易于表達矩陣，和matlab用法類似，是個強大的C++線性代數庫。而CLAPACK是線性代數包Lapack面向C/c++的接口。里面包含了很豐富的線性代數算法，包括廣義特征值求解接口，而且速度很快。我們希望將二者結合起來使用。

Eigen的安裝

Eigen直接以源代碼的方式提供給用戶，因此我們從官網上下載下后，直接在工程中包含其頭文件路徑即可。具體可參考：http://blog.csdn.net/abcjennifer/article/details/7781936

clapack的安裝

請查看官網，里面包含了詳細的使用與安裝步驟。

也可以使用我們已經編譯了的vc2010和vc2013的庫，可以點擊下載。

盡管clapack面向c語言，因此需要我們在包含頭文件的時候，記得加上extern “C”.但是最新的版本（比如CLAPACK 3.2.1）已經為我們在頭文件中加上了這些限制符，因此最新的版本可以兼容c和c++，所以直接在項目包含頭文件即可。

比如像下面一樣：

//Eigen
#include <Eigen/Dense>
#include <Eigen/Core>
#include <iostream>//clapack,必須放在Eigen后面#include <f2c.h>
#include <clapack.h>

而且應該注意Eigen與CLAPACK混合使用的時候，CLAPACK的頭文件要加在Eigen的后面。否則會出錯。

代碼

請查看Github主頁：https://github.com/xiamenwcy/EllipseFitting

實驗結果

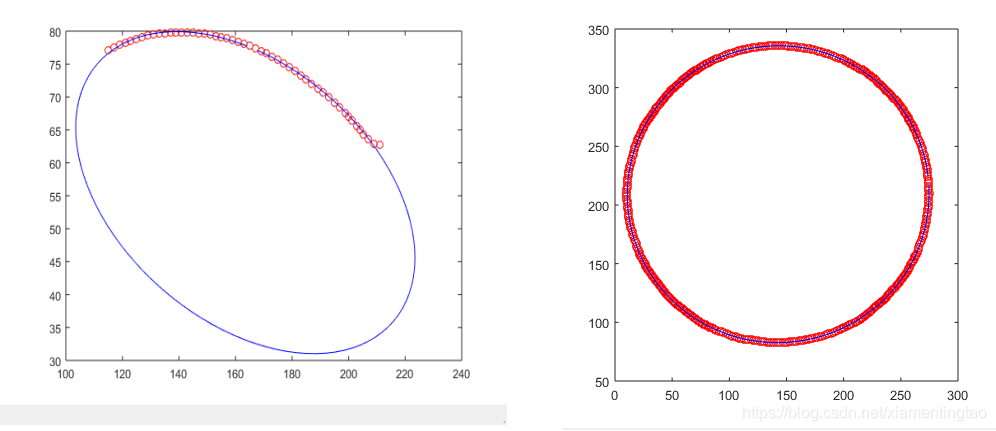
參考文獻

Eigen、LAPACK

1. Interfacing Eigen with LAPACK
2. Using BLAS/LAPACK from Eigen
3. CLAPACK for Windows
4. 如何在VC中調用CLAPACK
5. 使用Lapack庫的一些重要規則
6. 在VS中用CLAPACK解決廣義特征值問題
7. LAPACK 3.7.0
8. C＋＋編程：C++中同時使用Eigen和CLAPACK
9. CLAPACK在vc++6.0中成功調用
10. CLAPACK動態調用
11. Leading dimension
12. leading dimension 2

橢圓擬合

• Fitting an Ellipse to a Set of Data Points(python實現)
• 二次曲線Quadratic Curve
• fitellipse.cpp(opencv)
• Creating Bounding rotated boxes and ellipses for contours
• OpenCV’s fitEllipse() sometimes returns completely wrong ellipses
• Fitting an Ellipse to a Set of Data Points
• Direct Least Square Fitting of Ellipses (論文)
• best-fitting-line-circle-and-ellipse
• opencv中的橢圓擬合
• Python and C implementations of an ellipse fitting algorithm in double and fixed point precision.
• C++ code for circle fitting algorithms
• OriginDelight/EllipseFit (c++源碼)

論文作者，著名學者主頁：

• Bob Fisher： http://homepages.inf.ed.ac.uk/rbf/
• Fitzgibbon, Pilu, Fisher: Direct Least Squares Fitting of Ellipses：http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/FITZGIBBON/ELLIPSE/