今天是算法和數據結構專題的第22篇文章，我們一起來聊聊輾轉相除法。

輾轉相除法又名歐幾里得算法，是求最大公約數的一種算法，英文縮寫是gcd。所以如果你在大牛的代碼或者是書上看到gcd，要注意，這不是某某黨，而是指的輾轉相除法。

在介紹這個算法之前，我們先來看下最大公約數問題。

暴力解法

這個問題應該很明確了，我們之前數學課上都有講過。給我們紙筆讓我們求都沒有問題，分解因數找下共同的部分，很快就算出來了。但是用代碼實現怎么做呢？

用代碼實現的話，首先排除分解因數的方法。因為分解因數復雜度太高了，也很容易想明白，既然要分解因數，那么首先需要獲得一定量的質數吧。有了質數之后還要遍歷質數，將整數一點一點分解，顯然很麻煩，還不如直接暴力了。暴力解法并不復雜，我們直接從1開始遍歷，記錄下來同時能夠整除這兩個數的最大數即可。我們暴力的范圍也不大，從1到n。

很容易寫出代碼：

def gcd(a, b):    ret = 0    for i in range(min(a, b)):        if a % i == 0 and b % i == 0:            ret = i    return ret

這個很簡單，也許你可能還會想出一些優化，比如說首先判斷一下a和b之間是否有倍數關系，如果有的話直接就可以得到結果了。再比如說我們i的遍歷范圍其實可以不用到min(a, b)，如果a和b沒有倍數關系的話min(a, b) / 2就可以了。這些都是沒有問題的，但是即使加上了這些優化依然改變不了這是一個O(n)算法的本質。

比如說a是1e9，b是1e9-1，毫無疑問這樣的做法會超時。

輾轉相除法

接下來就輪到正主——輾轉相除法出場了，這個算法在《九章算術》當中曾經出現過，叫做更相減損術。不管叫什么，原理都是一樣的，它的最核心本質是下面這個式子：

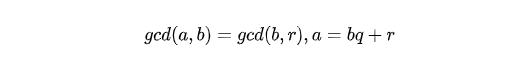
這個式子就是著名的歐幾里得定理，這里的r可以看成是a對b取余之后的結果，也就是說a和b的最大公約數等于b和r的最大公約數。這樣我們就把a和b的gcd轉移成了b和r，然后我們可以繼續轉移，直到這兩個數之間存在倍數關系的時候就找到了答案。

在我們寫代碼之前，我們先來看一下這個定理的證明。

我們假設u同時整除a和b，顯然這樣的u一定存在，因為u至少可以是1，所以：

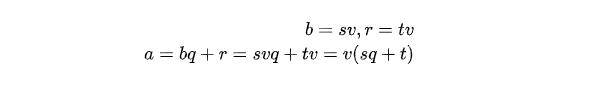
所以可以得到u也整除r，同樣我們可以證明能夠整除b和r的整數也可以整除a。我們假設v可以同時整除b和r：

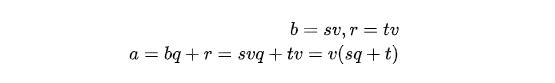
這樣我們就得到了v也可以整除a。也就是說a和b的每一個因子都是b和r的因子，同樣b和r的每一個因子也是a和b的因子，那么可以得出a和b的最大公約數就是b和r的最大公約數。

以上就是歐幾里得定理的簡單證明，如果看不懂也沒有關系，我們記住這個定理的內容就可以了。

接下來就是用代碼實現了，我們把這個公式套進遞歸當中非常容易：

def gcd(a, b):    if a < b:        a, b = b, a            if a % b == 0:        return b    return gcd(b, a % b)

我們首先判斷了a和b的大小關系，如果a小于b的話，我們就交換它們的值，保證a大于b。如果a和b取模的結果為0，那么說明a已經是b的倍數了，顯然它們之間的最大公約數就是b。

但其實我們沒有必要判斷a和b的大小，我們假設a小于b，那么顯然a % b = a，于是會遞歸調用b和a % b，也就是b和a，也就是說算法會自動調整兩者的順序。這么一來，這個代碼還可以進一步簡化，只需要一行代碼。

def gcd(a, b):    return a if b == 0 else gcd(b, a % b)

所以聽到有人說自己用一行代碼實現了一個算法，不要覺得它在裝逼，有可能他真的寫了一個gcd。

拓展歐幾里得

拓展歐幾里得本質上就是gcd，只是在此基礎上做了一定的拓展，從而來解決不定方程。不定方程就是ax + by = c的方程，方程要有解充要條件是(a, b) | c，也就是說a和b的最大公約數可以整除c。

也就是說求解ax + by = gcd(a, b)的解。假如說我們找到了這樣一組解x0和y0，那么x0 + (b / gcd) * t和y0 - (a / gcd) * t也是方程的解，這里的t可以取任意整數。

我們代入算一下即可：

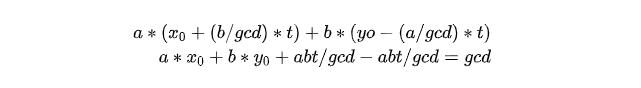
所以我們求出了這樣的x0和y0之后就相當于求出了無數組解，那么這個x0和y0怎么求呢，這就需要用到gcd算法了。

我們觀察一下gcd算法的遞歸代碼，可以發現算法的終止條件是a=gcd，b=0。對于這樣的a和b來說，我們已經找到了一組解使得ax+by=gcd，比如很明顯，x=1，y=0。實際上y可以為任何值，因為b=0。

我們回到遞歸的上一層的a和b，假設我們已經求出了b和a%b的最大公約數，并且求出了一組解x0和y0。使得b*x0 + (a%b)* y0 = gcd。那么我們能不能倒推得到a和b時候的解呢？

因為a % b = a - (a/b)*b，這里的/是整除計算的意思，我們代入：

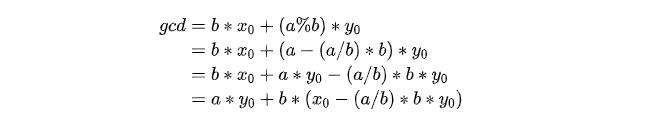
顯然對于a和b來說，它的一組解就是y0和x0 - (a/b)*b*y0，我們把這幾行計算加在代碼當中即可，非常簡單：

def exgcd(a, b, x=1, y=0):    # 當b=0的時候return    if b == 0:        return a, x, y    # 遞歸調用，獲取b, a%b時的gcd與通項解    gcd, x, y = exgcd(b, a%b, x, y)    # 代入，得到新的通項解    x, y = y, x - a//b*y    return gcd, x, y

這里我建議大家不要死記代碼，都去推導一下遞歸的這個推導公式。這個公式搞明白了，即使代碼記不住也沒有關系，后面臨時用到的時候再推導也可以。不然的話，即使背下來了代碼也不記得什么意思，如果碰到的場景稍微變動一下，可能還是做不出來。

逆元與解逆元

拓展歐幾里得算法我們理解了，但是好像看不出來它到底有什么用。一般情況下我們也碰不到讓我們計算通解的情況，但其實是有用的，用的最多的一個功能就是計算逆元。

在解釋逆元之前先來看一個問題，我們有兩個數a和b，和一個模底數p。我們可以得到(a + b) % p = (a%p + b%p)%p，也可以得到 (a - b)%p = (a%p - b%p)%p。甚至還可以得到 (a*b)% p =(a%p * b%p) %p，這些都是比較明確的，但是(a / b) % p = (a % p / b % p) % p，這個式子成立嗎？

最后的式子是不成立的，因為模數沒有除法的傳遞性，我們可以很方便舉出反例。比如a是20， b是10，p是4，(a/b)%p=2，而(a %p / b%p) % p = 0。

這就導致了一個問題，假如說我們在一連串計算當中，由于最終的結果特別大，我們無法存儲精確的值，希望存儲它關于一個模底數取模之后的結果。但是我們的計算當中又涉及除法，這個時候應該怎么辦？

這個時候就需要用到逆元了，逆元也叫做數論倒數。它其實起到一個和倒數類似的效果，假設a關于模底數p的逆元是x，那么可以得到：ax = 1 (mod p)

所以我們想要算 (a / b) % p，可以先求出b的逆元假設是inv(b)，然后轉化成(a%p * inv(b)%p)%p。

這個逆元顯然不會從天上掉下來，需要我們設計算法去求出來，這個用來求的算法就用到拓展歐幾里得，我們下面來看一下推導過程。

假設a和b互質，那么gcd(a, b) = 1，代入：

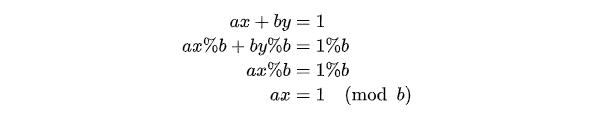
所以x是a關于b的逆元，反之可以證明y是b關于a的逆元。

這么計算是有前提的，就是a和b互質，也就是說a和b的最大公約數為1。否則的話這個計算是不成立的，也就是說a沒有逆元。那么整個求解逆元的過程其實就是調用拓展歐幾里得的過程，把問題說清楚花了很多筆墨，但是寫成代碼只有兩三行：

def cal_inv(a, m):    gcd, x, y = exgcd(a, m)    # 如果gcd不為1，那么說明沒有逆元，返回-1    return (x % m + m) % m if gcd == 1 else -1

在return的時候我們對x的值進行了縮放，這是因為x有可能得到的是負數，我們把它縮放到0到m的范圍當中。

逆元的求解方法除了拓展歐幾里得之外，還有一種算法，就是利用費馬小定理。根據費馬小定理，在m為質數的時候，可以得到

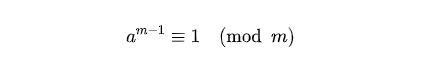
等式兩邊同時除以a，也就是乘上a的逆元，可以得到：

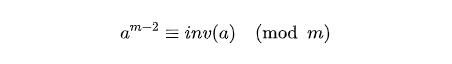
也就是說我們求出a^{m-2}然后再對m取模就得到了a的逆元，我們使用快速冪可以很方便地求出來。但是這個只有m為質數的時候才可以使用。

總結

今天我們聊了歐幾里得定理聊了輾轉相除法還聊了拓展歐幾里得和求解逆元，雖然這些內容單獨來看并不難，合在一篇文章當中量還是不小的。這些算法底層的基礎知識是數論，對于沒有參加過競賽的同學來說可能有些陌生，但是它也是算法領域一個很重要的分支。

如果喜歡本文，可以的話，請點個關注，給我一點鼓勵，也方便獲取更多文章。