圓上任意角度的點的坐標

如上圖，給定圓心（Cx,Cy）,半徑為R， 求$\theta$對應的點的坐標？ 此處$\theta$是相對于水平軸的角度。

顯然我們可以使用極坐標轉換來求：
$$\{\begin{array}{c}px=Cx+Rcos(\theta )\\ py=Cy+Rsin(\theta )\end{array}$$
注意如果以上豎直坐標系向下，此時變為圖像的坐標系，即

結果變成：

$$\{\begin{array}{c}px=Cx+Rcos(\theta )\\ py=Cy?Rsin(\theta )\end{array}$$
僅僅是y變了。

橢圓上任意角度的點的坐標

首先我們先來考慮標準橢圓上任意角度的點的坐標，再進行推廣。

已知主軸a（即橢圓箭頭所指方向對應的軸）,次軸b,求解與水平軸相交$\theta$對應的點的坐標？
$$\{\begin{array}{ccc}\frac{x^2}{a^2}+\frac{y^2}{b^2}& =& 1\\ \frac{y}{x}& =& \tan (\theta )\end{array}$$
將上面的第二式帶入第一式，可以求解得到：
$$x^2=\frac{a^2{b}^2}{b^2+a^2{\tan }^2(\theta )}$$
這時我們考慮$\theta$的范圍，可以得到：
(一). $0\le \theta <pi/2$ 或者 $\frac{3?pi}{2}<\theta \le 2?pi$
$$?\begin{array}{c}x=\frac{ab}{\sqrt{b^2+a^2{\tan }^2(\theta )}}\\ y=\frac{ab\tan (\theta )}{\sqrt{b^2+a^2{\tan }^2(\theta )}}\end{array}$$
(二). $pi/2<\theta <\frac{3?pi}{2}$
$$?\begin{array}{c}x=?\frac{ab}{\sqrt{b^2+a^2{\tan }^2(\theta )}}\\ y=?\frac{ab\tan (\theta )}{\sqrt{b^2+a^2{\tan }^2(\theta )}}\end{array}$$
(三). $\theta =pi/2$
$$\{\begin{array}{c}x=0\\ y=b\end{array}$$
(四). $\theta =\frac{3?pi}{2}$
$$\{\begin{array}{c}x=0\\ y=?b\end{array}$$
再考慮一般情況下的橢圓，如下：

如上$\theta \in [0,2?pi]$是相對于主軸的角度，$\alpha \in [?pi,pi]$, 不過我們一般僅僅考慮$\alpha \in [0,pi]$,求$\theta$對應的點的坐標？

基本思路就是先轉換成標準橢圓，再應用標準橢圓下的結果。

顯然我們需要將以上橢圓的中心移到原點，再繞原點旋轉$?\alpha$ ,即順時針旋轉$\alpha$，即：
$$\left(\begin{array}{c}x\\ y\end{array}\right)=R(\left(\begin{array}{c}X\\ Y\end{array}\right)?\left(\begin{array}{c}{X}_c\\ Y_c\end{array}\right))$$
其中
$$R=\left(\begin{array}{cc}cos(?\alpha )& ?sin(?\alpha )\\ sin(?\alpha )& cos(?\alpha )\end{array}\right)=\left(\begin{array}{cc}cos(\alpha )& sin(\alpha )\\ ?sin(\alpha )& cos(\alpha )\end{array}\right)$$
因此
$$\left(\begin{array}{c}X\\ Y\end{array}\right)=R^{?1}\left(\begin{array}{c}x\\ y\end{array}\right)+\left(\begin{array}{c}{X}_c\\ Y_c\end{array}\right)$$
其中
$$R^{?1}=R^T=\left(\begin{array}{cc}cos(\alpha )& ?sin(\alpha )\\ sin(\alpha )& cos(\alpha )\end{array}\right)(★)$$
這樣將前面$\left(\begin{array}{c}x\\ y\end{array}\right)$ 的四個結果應用過來，即得到傾斜的橢圓上的對應角度的點的坐標。

擴展：

1. 如果以上的角度是相對于水平軸的角度，則對應的橢圓上的點的坐標如何求呢？
   答： 其實很簡單，只需要：
   $${\theta }^{\prime }=\{\begin{array}{cc}\theta ?\alpha +2?pi,& \theta <\alpha \\ \theta ?\alpha ,& \theta \ge \alpha \end{array}$$
   將${\theta }^{\prime }$替換以上標準橢圓下的$\theta$即可。
2. 如果豎直坐標軸為豎直向下的，即為圖像坐標系下的橢圓，那么如何求對應的角度？
   答：
   需要做兩方面的改變即可：
   $$\{\begin{array}{c}\alpha \to ?\alpha \\ y\to ?y\end{array}$$
   第一行改變$★$出的$\alpha$. 第二行改變標準橢圓下的y值的符號。

matlab代碼

demo.m
################################
center_x=282;
center_y=263;
phi=pi/6;
R1=141;
R2=62;
%DrawEllipse([center_x,center_y],R1,R2,phi);
axis equal;
hold on;
set(gca,'ydir','reverse')
for angle=linspace(0,3*pi/2,360)[ px,py ] = get_points_ellipse(center_x, center_y,phi,R1,R2, angle );plot(px,py,'ro');hold on;
end
axis([0,500,0,500])

function [ px,py ] = get_points_ellipse(center_x, center_y,phi,R1,R2, angle )
% 求橢圓某個角度上的點的坐標。
%https://math.stackexchange.com/questions/22064/calculating-a-point-that-lies-on-an-ellipse-given-an-angle
%https://blog.csdn.net/xiamentingtao/article/details/54934467%https://stackoverflow.com/questions/17762077/how-to-find-the-point-on-ellipse-given-the-angle
%另一種解法  從極坐標的角度出發。% 橢圓參數  圓心 (center_x.center_y) 角度 phi(-pi,pi)，實際上僅考慮（0，pi） 沿著角度的主軸半徑R1，另一主軸對應的半徑R2
% 求相對于水平軸x軸上angle（基于0-2pi之間）上對應的點坐標。
% 注意求解的坐標系為：水平向右為x軸,豎直向上為y軸。 如果豎直向下為y軸，則下面的y應該變換成-y， phi變成-phi%先將斜的橢圓轉正，并平移到原點。方法就是平移到中心，且旋轉-phi角度,再應用標準橢圓求取點。
if(angle<phi)theta = angle-phi+2*pi;  %想對于主軸的角度
elsetheta = angle-phi;
end
% theta為相對于主軸的角度
alpha = -phi;    %與豎直的軸有關，如果是豎直向上，則變為正phi
% 先計算標準橢圓 x^2/R1^2+y^2/R2^2=1  與 直線 y/x=tan(angle)的交點。
assert(angle>=0 && angle<=2*pi);
if(theta==pi/2)x=0;y=R2;
elseif(theta==pi*3/2)x=0;y=-R2;
elseif(theta>pi/2 && theta<pi*3/2)x=-R1*R2/sqrt(R2^2+R1^2*tan(theta)^2);y=-R1*R2*tan(theta)/sqrt(R2^2+R1^2*tan(theta)^2);
elsex=R1*R2/sqrt(R2^2+R1^2*tan(theta)^2);y=R1*R2*tan(theta)/sqrt(R2^2+R1^2*tan(theta)^2); 
endy=-y;    %與豎直的軸有關，如果是豎直向上，則變為正y
% 將以上結果轉換回去
px= cos(alpha)*x-sin(alpha)*y+center_x;
py=sin(alpha)*x+cos(alpha)*y+center_y;end

function DrawEllipse(C,a,b,alpha)
% DRAWELLIPSE plots an ellipse
%   DrawEllipse(C,a,b,alpha) plots ellipse with center C, semiaxis a
%   and b and angle alpha between a and the x-axiss=sin(alpha); c=cos(alpha);
Q =[c -s; s c]; theta=[0:0.02:2*pi];
u=diag(C)*ones(2,length(theta)) + Q*[a*cos(theta); b*sin(theta)];
plot(u(1,:),u(2,:));
hold on;
plot(C(1),C(2),'+');

顯示結果，起點對應著角度為0。

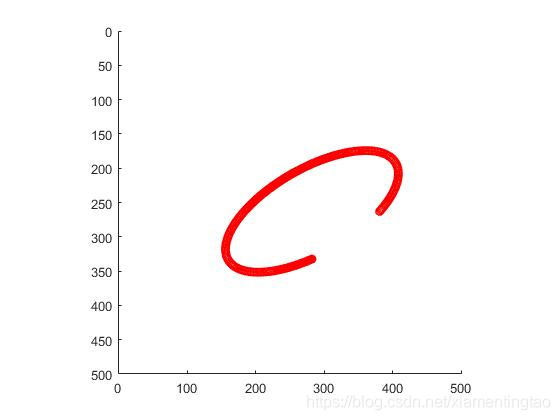
另一種基于極坐標變換的高效實現【轉載】

轉載： https://blog.csdn.net/he_zhidan/article/details/81347426
根據“圓心角”弧度（函數會將圓心角轉成離心角），獲取斜橢圓上的點坐標。ptCenter，橢圓中心；a橢圓長軸長度;b,橢圓短軸長度;radian，點于橢圓長軸夾角的弧度;dChangZhouAngle，長軸弧度

CDoublePoint2d GetPointOnEllipse(const CDoublePoint2d& ptCenter, double a, double b, double radian, double dChangZhouAngle)
{
const double dLiXin = atan2(asin(radian), bcos(radian));//離心角
double x = a*cos(dLiXin)cos(dChangZhouAngle) - bsin(dLiXin)sin(dChangZhouAngle) + ptCenter.x;
double y = acos(dLiXin)sin(dChangZhouAngle) + bsin(dLiXin)*cos(dChangZhouAngle) + ptCenter.y;
return CDoublePoint2d(x, y);
}

問題：

一，為什么不用atan？

答：atan的范圍是[-π/2,π/2]，atan2的范圍是(-π,π]。前者只能表示兩個象限，后者可以表示4個。

二，為什么不atan2(a*tan(radian),b)?

答：這樣寫，和用atan的效果一樣。

參考文獻

1. https://math.stackexchange.com/questions/22064/calculating-a-point-that-lies-on-an-ellipse-given-an-angle （主要參考這個）
2. https://stackoverflow.com/questions/17762077/how-to-find-the-point-on-ellipse-given-the-angle （這里有一個從極坐標變換角度新的推導）
3. https://blog.csdn.net/xiamentingtao/article/details/54934467