問題描寫敘述
平面上有N*M個格子,每一個格子中放著一定數量的蘋果。你從左上角的格子開始,每一步僅僅能向下走或是向右走,每次走到一個格子上就把格子里的蘋果收集起來,這樣下去,你最多能收集到多少個蘋果。
輸入:
第一行輸入行數和列數
然后逐行輸入每一個格子的中的蘋果的數量
輸出:
最多能收到的蘋果的個數。
思路分析
這是一個典型的二維數組DP問題
基本狀態:
當你到達第x行第y列的格子的時候,收集到的蘋果的數量dp[x][y]。
轉移方程:
因為你僅僅能向右走或者向下走,所以當你到達第x行第y列的格子的時候,你可能是從第x-1行第y列或者第x行第y-1列到達該格子的,而我們最后僅僅要收集蘋果最多的那一種方案。
所以:
dp[x][y] = max( if(x>0) dp[x-1][y] , if(y>0) dp[x][y-1])
編寫代碼
show you code:
#include<iostream>
#include<string.h>
using namespace std;
int a[100][100];
int dp[100][100];
int m,n;void dp_fun(int x,int y)
{dp[x][y] = a[x][y];int max = 0;if(x > 0 && max < dp[x-1][y]){max = dp[x-1][y];}if(y > 0 && max < dp[x][y-1]){max = dp[x][y-1];}dp[x][y] += max;if(x<m-1){dp_fun(x+1,y);} if(y<n-1){dp_fun(x,y+1);}return;
} int main()
{memset(dp,0,sizeof(dp)); cin>>m>>n;for(int i=0;i<m;i++){for(int j=0;j<n;j++){cin>>a[i][j];}} dp_fun(0,0);for(int i=0;i<m;i++){for(int j=0;j<n;j++){cout<<dp[i][j]<<"\t";}cout<<endl;}return 0;
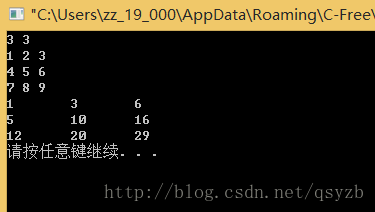
}演示樣例數據:















)



