===================================================================
一、二叉搜索樹（BSTree）的概念
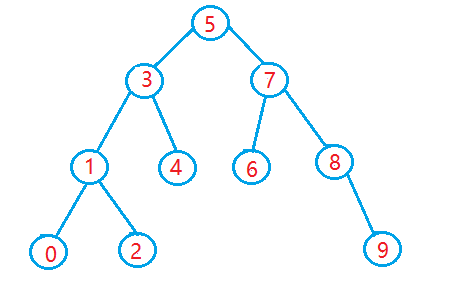
? ? ? ?二叉搜索樹又被稱為二叉排序樹，那么它本身也是一棵二叉樹，那么滿足以下性質的二叉樹就是二叉搜索樹：
? ? ? ?1、若左子樹不為空，則左子樹上左右節點的值都小于根節點的值
? ? ? ?2、若它的右子樹不為空，則它的右子樹上所有的節點的值都大于根節點的值
? ? ? ?3、它的左右子樹也要分別是二叉搜索樹
===================================================================
二、二叉搜索樹的插入
? 1、搜索
? ? ? ?插入之前我們先來說說它的搜索，像上圖這樣的一棵二叉搜索樹，我們要查找某一個元素是很簡單的。因為它的節點分布是有規律的，所以查找一棵元素只需要如下的步驟就可以了：
? ? ? ??
? ? ? ?2、插入
? ? ? ?由于二叉搜索樹的特殊性質確定了二叉搜索樹中每個元素只可能出現一次，所以在插入的過程中如果發現這個元素已經存在于二叉搜索樹中，就不進行插入。
否則就查找合適的位置進行插入。
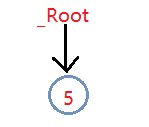
第一種情況：_root為空
直接插入，return ?true；
第二種情況：要插入的元素已經存在
如上面所說，如果在二叉搜索樹中已經存在該元素，則不再進行插入，直接return ?false；
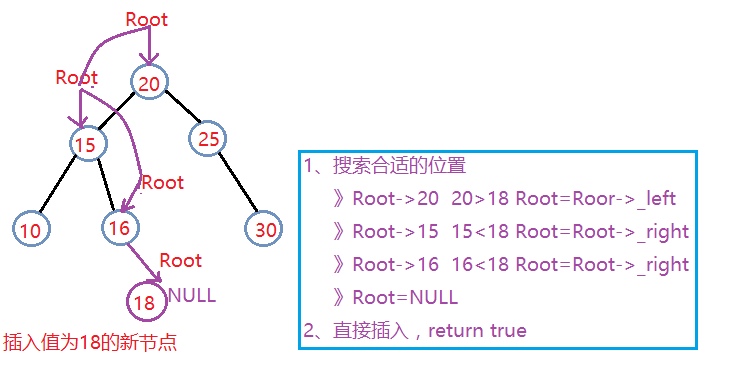
第三種情況：能夠找到合適位置
===================================================================
三、二叉搜索樹的刪除
對于二叉搜索樹的刪除操作，主要是要理解其中的幾種情況，寫起來還是比較簡單的。
當然一開始還是需要判斷要刪除的節點是否存在于我們的樹中，如果要刪除的元素都不在樹中，就直接返回false；否則，再分為以下四種情況來進行分析：
? ? ?》要刪除的節點無左右孩子
? ? ?》要刪除的節點只有左孩子
? ? ?》要刪除的節點只有右孩子
? ? ?》要刪除的節點有左、右孩子
?
刪除方法解釋：
? ? ?對于第一種情況，我們完全可以把它歸為第二或者第三種情況，就不用再單獨寫一部分代碼進行處理；
? ? ?》如果要刪除的節點只有左孩子，那么就讓該節點的父親結點指向該節點的左孩子，然后刪除該節點，返回true；
? ? ? ? ??
? ? ?》如果要刪除的節點只有右孩子，那么就讓該節點的父親結點指向該節點的右孩子，然后刪除該節點，返回true；
? ? ? ? ? ??
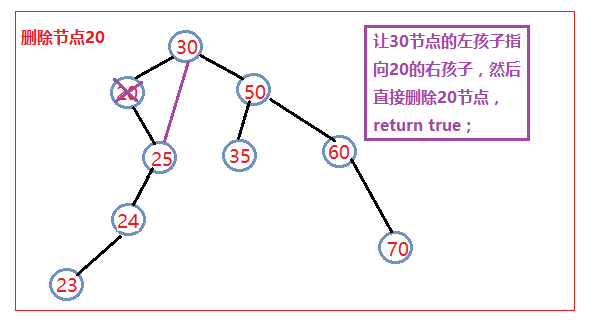
? ? ? ? ? 對于上面這兩種情況我們還應該在之前進行一個判斷，就是判斷這個節點是否是根節點，如果是根節點的話，就直接讓根節點指向這個節點的左孩子或右孩子，然后刪除這個節點。
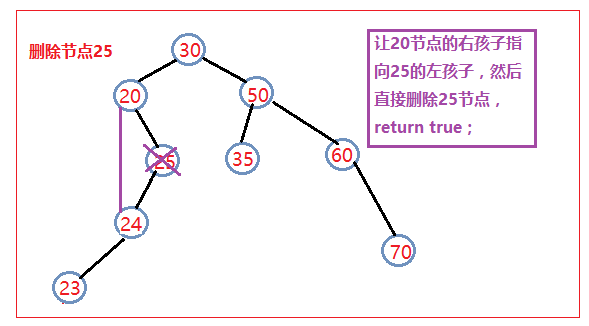
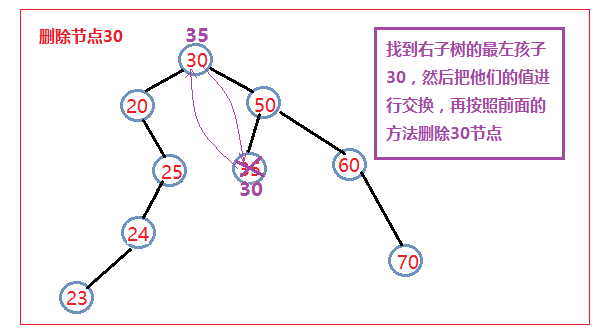
? ? ? ?》最后一種也是最麻煩的一種就是要刪除的節點的左右孩子都存在。此時我們的刪除方法如下：
? ? ? ? ? ?1、找到該節點的右子樹中的最左孩子（也就是右子樹中序遍歷的第一個節點）
? ? ? ? ? ?2、把它的值和要刪除的節點的值進行交換
? ? ? ? ? ?3、然后刪除這個節點即相當于把我們想刪除的節點刪除了，返回true；
===================================================================
程序代碼：
1、二叉搜索樹的插入操作
1 bool Insert(const K& key) 2 { 3 if (_root == NULL) 4 { 5 _root = new Node(key); 6 return true; 7 } 8 Node* parent=NULL; 9 Node* pcur = _root; 10 while (pcur) 11 { 12 if (pcur->_key == key) //有key節點，則不再插入 13 return false; 14 if (pcur->_key > key) 15 { 16 parent = pcur; 17 pcur = pcur->_left; 18 } 19 else if (pcur->_key < key) 20 { 21 parent = pcur; 22 pcur = pcur->_right; 23 } 24 } 25 if (parent->_key < key) 26 parent->_right = new Node(key); 27 else 28 parent->_left = new Node(key); 29 return true; 30 }
2、二叉搜索樹的刪除操作?bool Remove(const K& key)
1 bool Remove(const K& key) 2 { 3 assert(_root); 4 Node* parent = NULL; 5 Node* pcur = _root; 6 Node* del = pcur; 7 while (pcur != NULL && pcur->_key != key) 8 { 9 if (pcur->_key > key) 10 { 11 parent = pcur; 12 pcur = pcur->_left; 13 } 14 else if (pcur->_key < key) 15 { 16 parent = pcur; 17 pcur = pcur->_right; 18 } 19 } 20 if (pcur == NULL) 21 return false; 22 if (pcur->_left == NULL) //只有右孩子 23 { 24 //如果pcur就是根節點的話，讓根節點指向根的右 25 if (pcur == _root) 26 _root = pcur->_right; 27 else if (pcur == parent->_left) 28 { 29 parent->_left = pcur->_right; 30 } 31 else 32 { 33 parent->_right = pcur->_right; 34 } 35 del = pcur; 36 } 37 else if (pcur->_right == NULL) //只有左孩子 38 { 39 //如果是根節點，讓根節點指向根的左 40 if (pcur == _root) 41 _root = pcur->_left; 42 else if (parent->_left == pcur) 43 { 44 parent->_left = pcur->_left; 45 } 46 else 47 parent->_right = pcur->_left; 48 del = pcur; 49 } 50 //pcur左右孩子都不為空 51 else 52 { 53 //找到節點右子樹的最左節點 54 Node* left = pcur->_right; 55 parent = pcur; 56 while (left->_left) 57 { 58 parent=left; 59 left = left->_left; 60 } 61 del = left; 62 pcur->_key = left->_key; //交換節點的值 63 if (parent->_left == left) 64 { 65 parent->_left = left->_right; 66 } 67 else 68 { 69 parent->_right = left->_right; 70 } 71 72 } 73 delete del; 74 return true; 75 }
?
windows下安裝python及第三方庫numpy、scipy、matplotlib終極版)
