目錄

一、多層神經網絡

1、多層神經網絡數學模型

2、數學模型中的非線性函數fai

1）非線性函數fai存在的意義

2）非線性函數fai具體是什么？

3、多層神經網絡與單層神經網絡的區別與改進

1）單層神經網絡數學模型

2）多層神經網絡模型

3）區別

二、三層神經網絡

1、定理

2、一些概念（決策面、神經元、神經網絡層數）

1）決策面

2）神經元

3）神經網絡層數n

3、常見的三層神經網絡模型（含w,b的參數設置）

1）一個三角形決策面的神經網絡模型（兩層神經網絡）

2）一個四邊形決策面的神經網絡模型（兩層神經網絡）

3）一個曲線圍成決策面的神經網絡模型（兩層神經網絡）

小結1：一個決策面時最后一層常用w,b參數的設置

4)兩個決策面的神經網絡模型（三層神經網絡）

5)兩個以上決策面的神經網絡模型（三層神經網絡）

小結2：多個決策面時最后一層w,b常用參數和第二層w,b常用參數的設置

疑問：

---

一、多層神經網絡

1、多層神經網絡數學模型

并行化的系統

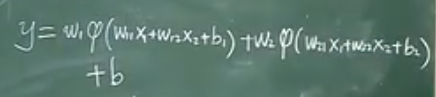
2、數學模型中的非線性函數fai

1）非線性函數fai存在的意義

如下圖可知如果沒有非線性函數最后得出的y依據是線性的，這就又回到了最初的單層神經網絡，沒有新的突破，而fai函數則圖突破了這個局限性

2）非線性函數fai具體是什么？

fai函數就是階躍函數

?

3、多層神經網絡與單層神經網絡的區別與改進

1）單層神經網絡數學模型

具體見：《機器學習——人工神經網絡之發展歷史（神經元數學模型、感知器算法）》

?

2）多層神經網絡模型

?

3）區別

多層神經網絡顧名思義具有多層的神經網絡，經過多層的變化后將輸入的xi變化后進行y的輸出

該多層神經網絡數學模型和階躍函數（fai函數）的結合可以解決所有的非線性問題，這也是多層神經網絡最大的優勢所在

?

二、三層神經網絡

1、定理

三層神經網絡可以模擬所有的決策面

2、一些概念（決策面、神經元、神經網絡層數）

1）決策面

決策面就是每一類樣本所分布的一塊區域，由多條線所圍成的一個區域（若由曲線圍成，可以將曲線看成由無數條非常短的線組成的曲線）

三條線圍成一個決策面（C1類的區域）

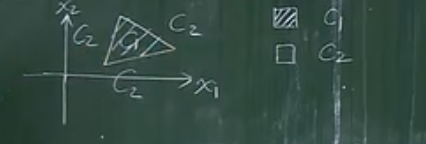
四條線圍成一個決策面（C1類的區域）

曲線圍成一個決策面（C1類的區域）——將曲線看成由無數直線構成

直線圍成多個分開的決策面（C1類的區域）

?

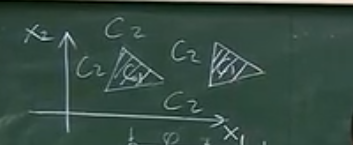
2）神經元

神經元在數學模型中的位置如下圖所示，神經元的個數其實就是圍成決策面的直線條數，圍成決策面的條數有多少，那么神經元就有多少個，若是曲線，則有無數個神經元

3）神經網絡層數n

神經網絡層數一般由決策面的個數決定，若決策面只有一個，神經網絡數學模型采用兩層神經網絡就可以實現，但是如果決策面有多個（如上面的C1類的區域分開成了兩個決策面）則神經網絡數學模型采用三層神經網絡就可以實現

決策面個數m，則神經網絡層數n：

所以三層神經網絡可以模擬所有的決策面

?

3、常見的三層神經網絡模型（含w,b的參數設置）

1）一個三角形決策面的神經網絡模型（兩層神經網絡）

?

2）一個四邊形決策面的神經網絡模型（兩層神經網絡）

?

3）一個曲線圍成決策面的神經網絡模型（兩層神經網絡）

將曲線用無數個非常短的線去替代曲線，只是神經元為無限個

?

小結1：一個決策面時最后一層常用w,b參數的設置

答：設決策面為1個，圍成決策面的直線條數為n，則取：所有w = 1 ; b = - n + 0.5

只有一個決策面的數學模型最后一層神經網絡是與邏輯關系，即所有輸入為1，歸類為C1，反之歸類為C2

?

4)兩個決策面的神經網絡模型（三層神經網絡）

一個決策面的神經元在第二層的輸出為一個，有多少個決策面第二層就會有多少個輸出（與關系）

5)兩個以上決策面的神經網絡模型（三層神經網絡）

兩個以上的決策面的神經網絡模型和兩個決策面是類似的，只是第一層的神經元數目多了，第二層的與關系多了而已

?

小結2：多個決策面時最后一層w,b常用參數和第二層w,b常用參數的設置

答：多個決策面時，最后一層的w,b參數固定為：w = 1 , b = -0.5

第二層每個與關系處即每一個決策面的第二層的w,b參數設置參考上面的小結1

疑問：

那么該怎么取利用這個神經網絡模型去解決實際的問題呢？至今為止神經網絡的理論還不夠完善，大部分還是通過實驗的方式來獲得神經網絡模型中的參數（主要是第一層中的w,b參數），也因為這樣，神經網絡成為了一個實驗性的學科，但是也有常用的神經網絡模型訓練方法（訓練就是通過訓練樣本求解參數的一個過程，，進而獲得完整的模型，利用模型可以對測試樣本進行分類），可以參見文章：《機器學習——人工神經網絡之后向傳播算法（BP算法）》