對于△ABC證明：
????①三角形的三條中線交于一點：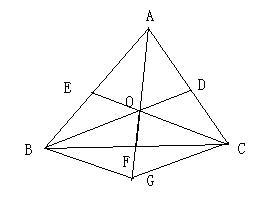
????等腰三角形：作中線BD、CE與AC、AB交于D、E，相交于O，連接AO并延長交BC于F；
?????????????????????????證△ABD全等于△ACE，再證△EBO全等于△DCO，得BO=CO，又AB=AC，所以AF為△ABC的中線；
????普通三角形：在前面的基礎上過B作CG∥BD，交AF的延長線于G，連接AG；
?????????????????????????易證O為AG中點（用相似），再得BG∥CE，即四邊形BGCO為平行四邊形，F為對角線交點，得BF=CF，所以AF為△ABC的中線；
????②三角形的三條高交于一點：
????銳角三角形：作三條高AD、BE、CF，BD與AF交于O1、CE與BD交于O2、AF與CE交于O3；
?????????????????????????用相似證得AD*AC=AE*AB、AO1*AF=AD*AC、AO3*AF=AE*AB，等量代換得AO1*AF=AO3*AF，即AO1=AO3，O1、O3重合，則它們也與O2重合，所以三角形的三條高交于一點；
????鈍角三角形：自己證吧！
????③三角形三條角平分線交于一點：
?????三角形兩條角平分線的交點到三角形三邊距離相等，則這個交點與第三邊連線為角平分線，所以三角形三條角平分線交于一點；
????④三角形三邊垂直平分線交于一點：?????三角形兩條垂直平分線的交點與三角形三點所連線段相等，則這個交點也在第三邊的垂直平分線上，所以三角形三邊垂直平分線交于一點；
另外，塞瓦定理和向量可以直接秒殺……
????完……?
?
分組表格控件--GroupingGrid（轉）)
