? ? ? ?先來張《計算機視覺:算法與應用》中的3D重建示例圖鎮樓!
? ? ? ? ?好吧,現在言歸正傳,來看看幾何學上世界是怎樣投影進攝相機里的吧!接下來讓我們來看一下本系列博客的第一“搏”:
圖像坐標:我想和世界坐標談談(A)
???????? 首先,我先解釋一下這個題目吧。題目的字面意義是說:圖像坐標系想和世界坐標系談談。這里面包含著兩個問題:
? ? ? ? ?A、談話對象:視覺系統的三大坐標系:世界坐標系,攝像機坐標系和圖像坐標系。這是玉米在本文《我想和世界坐標談談 ? ? ? ? ? ? ? ? ? ? ? (A)》中想要和大家分享的內容。其中主要包含:三大坐標系的位置、作用和應用場景。
? ? ? ? ?B、談話方式:兩個不同的坐標系之間該如何溝通呢?玉米將在《我想和世界坐標談談(B)》中和大家分享一下剛體變換和透視 ? ? ? ? ? ? ? ? 投影變換。連起兩個坐標系之間這不在一個參考系的“世界上最遠的距離”。
? ? ? ? ? ? ? ? ?好吧,下面讓我們來揭開三大坐標系的廬山真面目。
?
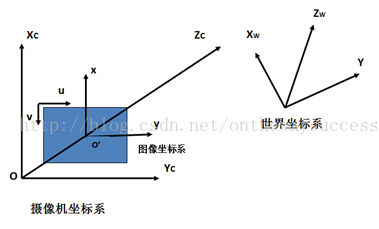
? ? ? ? ?上圖是三個坐標的示意簡圖,通過它大家可以對三個坐標有一個直觀的認識。下面來看看三個坐標系的骨子里藏了什么。
? ? ? ? ?世界坐標系(XW,YW,ZW):其是目標物體位置的參考系。除了無窮遠,世界坐標可以根據運算方便與否自由放置。在雙目視覺中世界坐標系主要有三個用途:1、標定時確定標定物的位置2、作為雙目視覺的系統參考系,給出兩個攝像機相對世界坐標系的關系,從而求出相機之間的相對關系3、作為重建得到三維坐標的容器,盛放重建后的物體的三維坐標。世界坐標系是將看見中物體納入運算的第一站。
? ? ? ? 攝像機坐標系(XC,YC,ZC):其是攝像機站在自己角度上衡量的物體的坐標系。攝像機坐標系的原點在攝像機的光心上,z軸與攝像機光軸平行。它是與拍攝物體發生聯系的橋頭堡,世界坐標系下的物體需先經歷剛體變化轉到攝像機坐標系,然后在和圖像坐標系發生關系。它是圖像坐標與世界坐標之間發生關系的紐帶,溝通了世界上最遠的距離。哈哈
? ? ? ? ?圖像坐標系(x,y)/(u,v) :其是以攝像機拍攝的二維照片為基準建立的坐標系。用于指定物體在照片中的位置。玉米更傾向將(x,y)稱為連續圖像坐標或空間圖像坐標,將(u,v)稱為離散圖像坐標系或者是像素圖像坐標系(雖然這樣的稱呼未經考證,但更能傳達二者的物理意義)。
? ? ? ? ? (x,y)坐標系的原點位于攝像機光軸與成像平面的焦點O’(u0,v0)上,單位為長度單位(米)。(u,v)坐標系的原點在圖片的左上角(其實是存儲器的首地址)如上圖所示,單位為數量單位(個)。(x,y)主要用于表征物體從攝像機坐標系向圖像坐標系的透視投影關系。而(u,v)則是實實在在的,我們能從攝像機中得到的真實信息。
(x,y)與(u,v)存在如下轉換關系:
? ? ? ? ? dx代表x軸方向一個像素的寬度,dy代表y軸方向上一個像素的寬度。dx、dy為攝像機的內參數。(u0,v0)稱為圖像平面的主點,也是攝像機的內參數。其實相當于對x軸和y軸的離散化。其可以運用齊次坐標,將上式寫成矩陣形式,如下:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?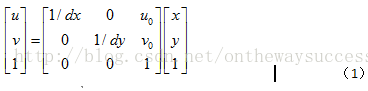
? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
? ? ? (1)式運用了齊次坐標,初學者可能會感到有些迷惑。大家會問:怎樣將普通坐標轉換為齊次坐標呢?齊次坐標能帶來什么好處呢?
? ? ? ? ?玉米在這里對齊次坐標做一個通俗的解釋。此處只講怎么將普通坐標改寫為齊次坐標及為什么引入齊次坐標。這里只做一個通俗但不太嚴謹的表述。力求簡單明了。針對齊次坐標的嚴謹的純數學推導,可參見“周興和版的《高等幾何》---1.3拓廣平面上的齊次坐標”。玉米曾詳細讀過《高等幾何》這本書,但覺得離計算機視覺有點遠,是講純數學的投影關系的,較為生澀難懂。
? ? ? ? 齊次坐標可以理解為在原有坐標后面加一個“小尾巴”。將普通坐標轉換為齊次坐標,通常就是在增加一個維度,這個維度上的數值為1。如圖像坐標系(u,v)轉換為(u,v,1)一樣。對于無窮遠點,小尾巴為0。注意,給零向量增加小尾巴,數學上無意義。
那么,為什么計算機視覺在坐標運算時要加上這個“小尾巴”呢?
? ? ? ? 玉米看來有兩點原因:
? ? ? ? ?1、 將投影平面擴展到無窮遠點。如對消隱點(vanishing point)的描述。
? ? ? ? ? 2、 使得計算更加規整
? ? ? ? ?如式(1)如果用普通坐標來表達的話,會是下面的樣子:
? ? ? ? ? 這樣的運算形式會給后與運算帶來一定的麻煩,所以齊次坐標是一個更好的選擇。
? ? ? ? ? 齊次坐標還有一個重要的性質,伸縮不變性。即:設齊次坐標M,則αM=M。

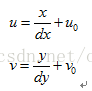
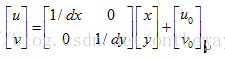



)









)

)


合并分支的方法與策略)
